Связь между продольными и поперечными составляющими электромагнитного поля

Будем рассматривать производную, бесконечно длинную направляющую систему, ориентированную вдоль оси Z.

Будем полагать:

1. Форма поперечного сечения не зависит от Z - линия однородна, кроме того, параметры среды и граничные условия, которым удовлетворяют поля, не зависят от Z.

2. Направляющая система не вносит потерь.

Мы уже рассматривали направленные волны над границей раздела, характер изменения E и H вдоль продольных и поперечных координат был различным.

Введем два параметра:

1. Продольное волновое число .

2. Поперечное волновое число т.е. .

Особенность направляемых волн: комплексная амплитуда каждой из шести проекций векторов Е и Н зависит от пространственных координат по закону:

Начальную фазу волны всегда можно подобрать так, чтобы - была действительной.

Производные по Z:

(3.1)

Сторонние источники отсутствуют и поле описывается Уравнениями Максвелла:

Развернем эти уравнения в декартовой системе координат. Из первого уравнения Максвелла:

;

;

Из второго уравнения Максвелла:

;

;

Решим эти уравнения относительно Е (например, совместно первое и пятое уравнение):

; ; ; (3.2)

Аналогично в любой другой системе координат.

Итак, достаточно найти лишь две функции для любой направляющей системы, а остальные проекции определяют через них

Прямоугольный металлический волновод

Прямоугольный металлический волновод э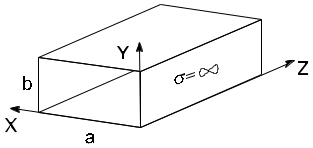 то полая металлическая идеально проводящая ( ) труба с поперечным сечением прямоугольной формы.

Будем полагать, что волновод заполнен средой с параметрами (воздух) . Найдем все типы электромагнитных волн, которые могут существовать внутри волновода на всем протяжении оси (как они созданы пока не рассматриваем).

Волны типа – H:

Для этих волн характерно . Тогда из системы (3.2):

; ;

; (3.3)

Где функция является решением уравнения Гельмгольца ( - производные только по поперечным координатам):

, где и отыскивается в виде: .

При решении следует учитывать граничные условия (тангенциальная составляющая Е на металле обращается в 0):

при y = 0, y = b

при x = 0, x = а

При решении удобнее выразить их через :

при у = 0, у = b

при x = 0, x = а

Таким образом, надо решить краевую задачу Неймана (в ноль обращается производная, иначе Дирихле).

Используем метод Фурье, представляем в виде:

,

подставляем его в уравнение Гельмгольца:

,

разделим это уравнение на неизвестное решение:

.

g - не зависит от X и Y, поэтому, чтобы последнее уравнение выполнялось при всех X и Y, надо чтобы:

, ,

где - некоторые числа удовлетворяющие: .

Общие решения двух последних уравнений выражаются через гармонические функции:

;

.

Отсюда: .

Остается выбрать шесть величин A, B, C, D, , так, чтобы выполнялись граничные условия на стенках волновода.

Граничные условия при X = 0 и Y = 0 будут выполнятся, если А = С = 0.

Произведение двух оставшихся амплитудных коэффициентов можно обозначить через и тогда:

.

Теперь остается подобрать величины так, чтобы граничные условия выполнялись при

X = а и Y = b:

; g ;

Где m и n – любые целые положительные числа не равные нулю одновременно (иначе силовые линии магнитного поля Н - незамкнуты и нарушается четвертое уравнение Максвелла).

Краевая задача имеет решения отличные от нуля только при условии:

.

Каждому значению g, (собственное значение) соответствует одно из множества решений уравнений Максвелла, которое в данном случае называют волной , где m и n – индексы волны данного типа. Физически они означают количества стоячих полуволн, возникающих внутри волновода вдоль координатных осей x и y соответственно.