- •4. Метод координатных сеток.
- •Режущий инструмент
- •6. Строгание
- •7. Методы нарезания резьб.
- •8. Глубинное шлифование.
- •10. Основные факторы. Влияющие на точность получения геометрических размеров.
- •11. Плосоке шлифование по принципу карусельных станков.
- •21. Шеверы
- •16. Методика статической балансировки шлифовального круга.
- •Технология
- •Сущность групповой обработки деталей.
- •Методы сборки.
ТЕОРИЯ РЕЗАНИЯ
2. Поляризационно-оптический метод исследования напряжении, метод изучения напряжений в деталях машин и строительных конструкциях на прозрачных моделях. Основан на свойстве большинства прозрачных изотропных материалов (стекло, целлулоид, желатин, пластмассы - оптически чувствительные или пьезооптические материалы) становиться при деформации оптически анизотропными, т. е. на возникновении искусственного двойного лучепреломления (т. н. пьезооптического эффекта). Главные значения тензора диэлектрической проницаемости линейно связаны с главными напряжениями. Так, например, для пластинки, нагруженной в своей плоскости, одно главное напряжение sз, направленное нормально к пластинке (рис. 1, а), равно нулю и одна из главных плоскостей оптической симметрии совпадает с плоскостью пластинки. Если на пластинку D в круговом полярископе (рис. 2) падает свет перпендикулярно к её плоскости, то оптическая разность хода равна: D = d (n1 - n2) или D = cd (s1 - s2), где d - толщина пластинки, (s1 и s2 - главные напряжения, с - т. н. относительный оптический коэффициент напряжений. Это уравнение (т. н. уравнение Вертгейма) - основное при решении плоских задач П.-о. м. и. При просвечивании монохроматическим светом в точках интерференционного изображения модели, в которых D = ml (m - целое число), наблюдается погашение света; в точках, где D = (2m + 1)l/2, - максимальная освещённость. На изображении модели (рис. 3) получаются светлые и тёмные полосы разных порядков m (картина полос). Точки, лежащие на одной и той же полосе, имеют одинаковую D, т. е. одинаковые s1 - s2 = 2tмах = D/cd (гдеtмах - максимальные скалывающие напряжения). При белом свете точки с одинаковыми tmax соединяются линиями одинаковой окраски - изохромами. Для определения s1 - s2 (или tmax) в данной точке достаточно определить с для материала модели и измерить компенсатором D или можно определить (s0 модели и подсчитать порядок полосы m (s0 = l/cd - разность главных напряжений в модели, вызывающих разность хода D = l; с и s0 получают при простом растяжении, сжатии или чистом изгибе на образцах из материала модели). Т. к. при нормальном просвечивании плоской модели можно получить только разность главных напряжений и их направление, то для определения (s1 и s2 в отдельности существуют дополнительные физико-механические способы измерения (s1 + s2, а также графовычислительные методы разделения (s1 и s2 по известным s1 - s2 и их направлению, использующие уравнения механики сплошной среды. Для исследования напряжений на объёмных моделях применяется более сложная техника эксперимента. Объёмная модель часто исследуется с применением метода «замораживания» деформаций. Модель из материала, обладающего свойством «замораживания» (отверждённые эпоксидные, фенолформальдегидные смолы и др.), нагревается до температуры высокоэластического состояния, нагружается и под нагрузкой охлаждается до комнатной температуры (температуры стеклования). После снятия нагрузки деформации, возникающие в высокоэластическом состоянии, и сопровождающая их оптическая анизотропия фиксируются. Наглядно описать это явление можно при помощи условной двухфазной модели материала. При нагреве до 80-120 °С (высокоэластическое состояние) одна часть материала размягчается, другая остаётся упругой. Нагрузке, приложенной к нагретой модели, противостоит неразмягчающийся скелет. При охлаждении нагруженной модели до комнатной температуры размягчающаяся часть снова застывает («замораживается») и удерживает деформацию в скелете после снятия нагрузки. «Замороженную» модель распиливают на тонкие пластинки (срезы) толщиной 0,6- 2 мм, которые исследуют в обычном полярископе. Применяется также метод рассеянного света, при котором тонкий пучок параллельных лучей поляризованного света пропускается через объёмную модель и даёт в каждой точке на своём пути рассеянный свет, который наблюдается в направлении, перпендикулярном к пучку. Состояние поляризации по линии каждого луча от точки к точке меняется соответственно напряжениям в этих точках. Существует метод, при котором в изготовленную из оптически нечувствительного к напряжениям прозрачного материала (специальные органические стекла) объёмную модель вклеивают тонкие пластинки из оптически чувствительного материала. Измерения во вклейках проводят, как на плоской модели, - с просвечиванием нормально или под углом к поверхности вклейки. Описанный П.-о. м. и. применяется для изучения напряжений в плоских и объёмных деталях в пределах упругости в тех случаях, когда применение вычислительных методов затруднено или невозможно. П.-о. м. и. напряжений используется для изучения пластических деформаций (фотопластичность), динамических процессов, температурных напряжений (фототермоупругость), для моделирования при решении задач ползучести (фотоползучесть) и др. нелинейных задач механики деформируемого тела. Разработан также метод оптически чувствительных наклеек (слоев), наносимых на поверхности натурных деталей. Слой оптически чувствительного материала наносится на поверхность металлической детали или её модели в жидком виде и затем подвергается полимеризации или наклеивается на деталь в виде пластинки; это обеспечивает равенство деформаций нагруженной детали и покрытия. Деформации в покрытии определяются по измеренной в нём разности хода в отражённом свете при помощи односторонних полярископов. Так как П.-о. м. и. напряжений ведутся на моделях, то они заканчиваются переходом от напряжений в модели к напряжениям в детали. В простейшем случае sдет = sмод b/a2, где a и b - масштабы геометрического и силового подобий.
4. Метод координатных сеток.
Для подтверждения высказанных предположений воспользуемся методом координат-
ных сеток [7], который позволяет определить интенсивность деформаций. Суть метода со-
стоит в нанесении координатной сетки на поперечное сечение составного образца (рис.1).
Шаг сетки выбран, таким чтобы дальнейший расчет по аналитическим зависимостям показал
адекватные значения рассчитываемых параметров и составил 3 мм. Материал для исследова-
ния принят С1.
РЕЗЦЫ
Резцы являются одним из простых и наиболее распространенных металлорежущих инструментов. Основные определения для обработки резцами даны в ГОСТ 25751-83.
Резец состоит из головки, т. е. рабочей части, и тела или стержня, служащего для закрепления резца (рисунок 1.1) в резцедержателе станка или в другом крепежном устройстве.
|
Рисунок 1.1 – Конструкция резца |
Головка резца состоит из следующих элементов: 1) передней поверхности (грани); 2) задней поверхности (грани); 3) режущих кромок; 4) вершины.
Передней поверхностью называется поверхность резца, по которой сходит стружка.
Задними поверхностями называются поверхности, обращенные к обрабатываемой заготовке. Их две – главная и вспомогательная.
Режущие кромки образуются пересечением передней и задних поверхностей. Их две – главная режущая кромка и вспомогательная.
Главная режущая кромка выполняет главную работу резания. Она образуется от пересечения передней и главной задней поверхностей. Вспомогательная режущая кромка образуется от пересечения передней и вспомогательной задней поверхностей. Вспомогательных режущих кромок может быть две (например, у отрезного резца).
Вершиной резца является место сопряжения главной режущей кромки со вспомогательной.
Форма режущей части резца определяется конфигурацией и расположением передней и задней поверхностей. Расположение указанных поверхностей и режущих кромок в пространстве характеризуется рядом углов, называемых углами резца.
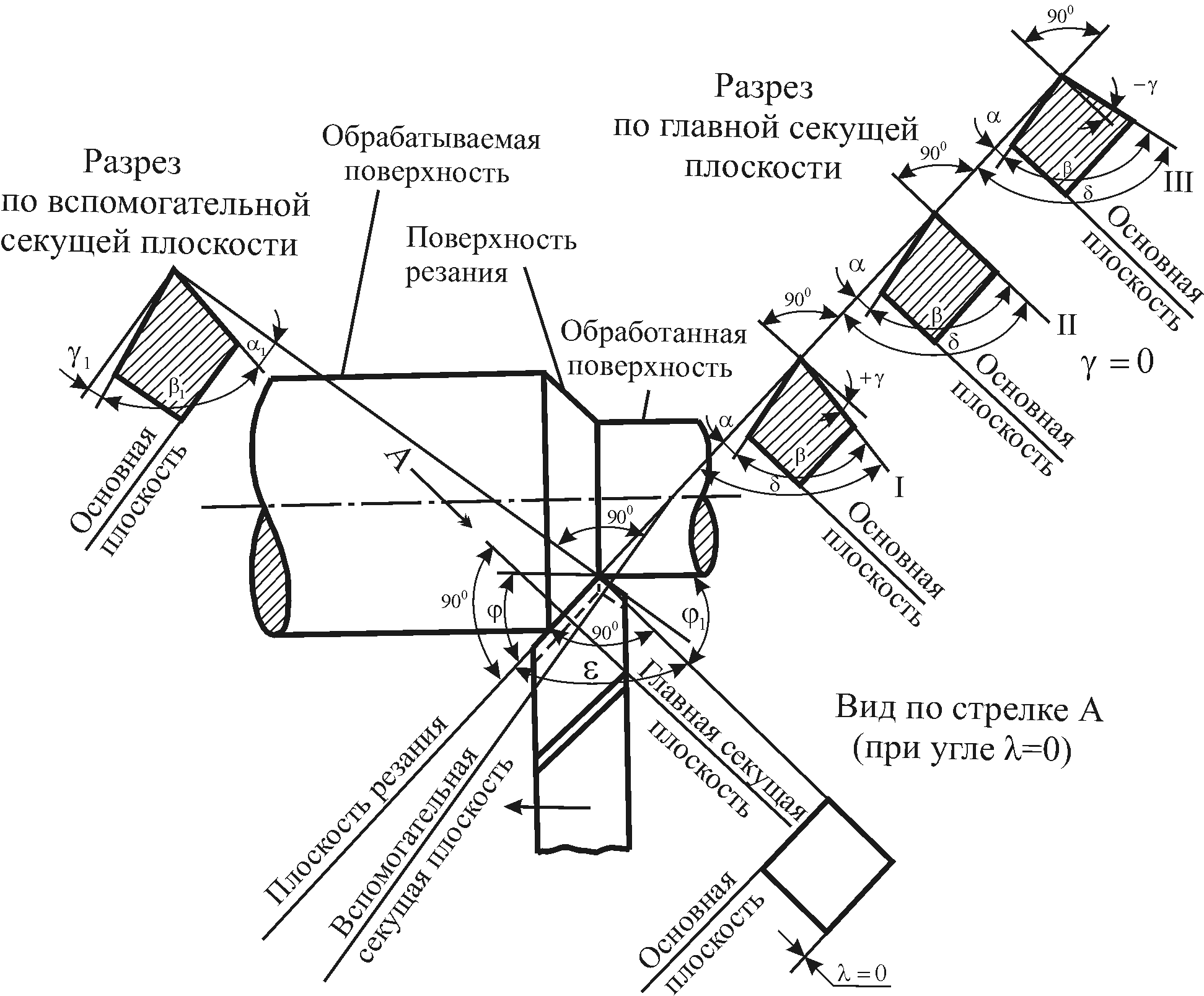
Исходной базой для измерения углов являются две плоскости: основная плоскость 5 и плоскость резания 4, указанные на рисунке 1.2.
|
|
На рисунке 1.2 обозначены также три поверхности детали: обрабатываемая поверхность 1, поверхность резания 2 и обработанная поверхность 3.
Плоскость резания 4 – плоскость, касательная к поверхности резания и проходящая через главную режущую кромку.
Основная плоскость 5 – плоскость, параллельная направлениям продольной и поперечной подач резца.
Главная секущая плоскость – плоскость, перпендикулярная к проекции главной режущей кромки на основную плоскость.
Проходные |
Подрезные |
Прорезные |
Отрезные Галтельные |
|
|
|
|
|
|
Резьбовые |
Расточные |
Фасочные |
Фасонные |
|
|
|
|
|
|
Углы резца
Режущая часть резца имеет форму клина, заточенного под определенными углами.
Углы резца делятся на главные и вспомогательные.
Главные
углы измеряются в главной секущей
плоскости. К главным углам резца относятся
задний угол
 ,
угол заострения
,
угол заострения
 ,
передний угол
,
передний угол
 и угол резания
и угол резания
 .
.
На рисунке 1.11 дана рабочая часть резца с необходимыми сечениями, где показаны главные и вспомогательные углы:
а) – главный передним углом называется угол между передней поверхностью резца и плоскостью, перпендикулярной к плоскости резания, проведенной через главную режущую кромку. Он может быть положительным, когда передняя поверхность направлена вниз от плоскости, перпендикулярной к плоскости резания равным нулю, когда передняя поверхность перпендикулярна плоскости резания (рисунок 1.11);
б) – главным задним углом называется угол между главной задней поверхностью резца и плоскостью резания;
в) – углом резания называется угол между передней поверхностью резца и плоскостью резания.
г) – главный угол заострения называется угол между передней и главной задней поверхностью резца.
|
Рисунок 1.11 – Основные углы резца |
При положительном значении между углами существует зависимость
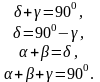
При положительном значении
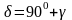 .
.
Кроме рассмотренных главных углов, резец характеризуется вспомогательными: передним углам, углами в плане и углом наклона главной режущей кромки.
Вспомогательные углы измеряются во вспомогательной секущей плоскости.
Вспомогательная секущая плоскость – это плоскость, перпендикулярная к проекции вспомогательной режущей кромки на основную плоскость.
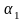 – вспомогательный
задний угол называется угол между
вспомогательной задней поверхностью
и плоскостью, проходящей через
вспомогательную режущую кромку,
перпендикулярную основной плоскости.
– вспомогательный
задний угол называется угол между
вспомогательной задней поверхностью
и плоскостью, проходящей через
вспомогательную режущую кромку,
перпендикулярную основной плоскости.
Положение режущих кромок определяется углами в плане (рисунок 1.11):
а)
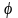 – главный угол в плане – угол между
проекцией главной режущей кромки на
основную плоскость и направлением
подачи (угол между плоскостью резания
и рабочей плоскостью);
– главный угол в плане – угол между
проекцией главной режущей кромки на
основную плоскость и направлением
подачи (угол между плоскостью резания
и рабочей плоскостью);
б)
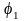 – вспомогательный угол в плане – угол
между проекцией вспомогательной режущей
кромки на основную плоскость и направлением
подачи (угол между рабочей плоскостью
и проекцией вспомогательной режущей
кромки на основную плоскость);
– вспомогательный угол в плане – угол
между проекцией вспомогательной режущей
кромки на основную плоскость и направлением
подачи (угол между рабочей плоскостью
и проекцией вспомогательной режущей
кромки на основную плоскость);
в)
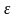 – угол при вершине – угол между проекциями
главной и вспомогательной режущих
кромок на основную плоскость;
– угол при вершине – угол между проекциями
главной и вспомогательной режущих
кромок на основную плоскость;
Очевидно, что + + 1 = 180.
г)
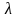 –
угол
наклона главной режущей кромки – угол,
заключенный между главной режущей
кромкой и линией, проведенной через
вершину резца параллельно основной
плоскости (угол между главной режущей
кромкой и основной плоскостью).
–
угол
наклона главной режущей кромки – угол,
заключенный между главной режущей
кромкой и линией, проведенной через
вершину резца параллельно основной
плоскости (угол между главной режущей
кромкой и основной плоскостью).
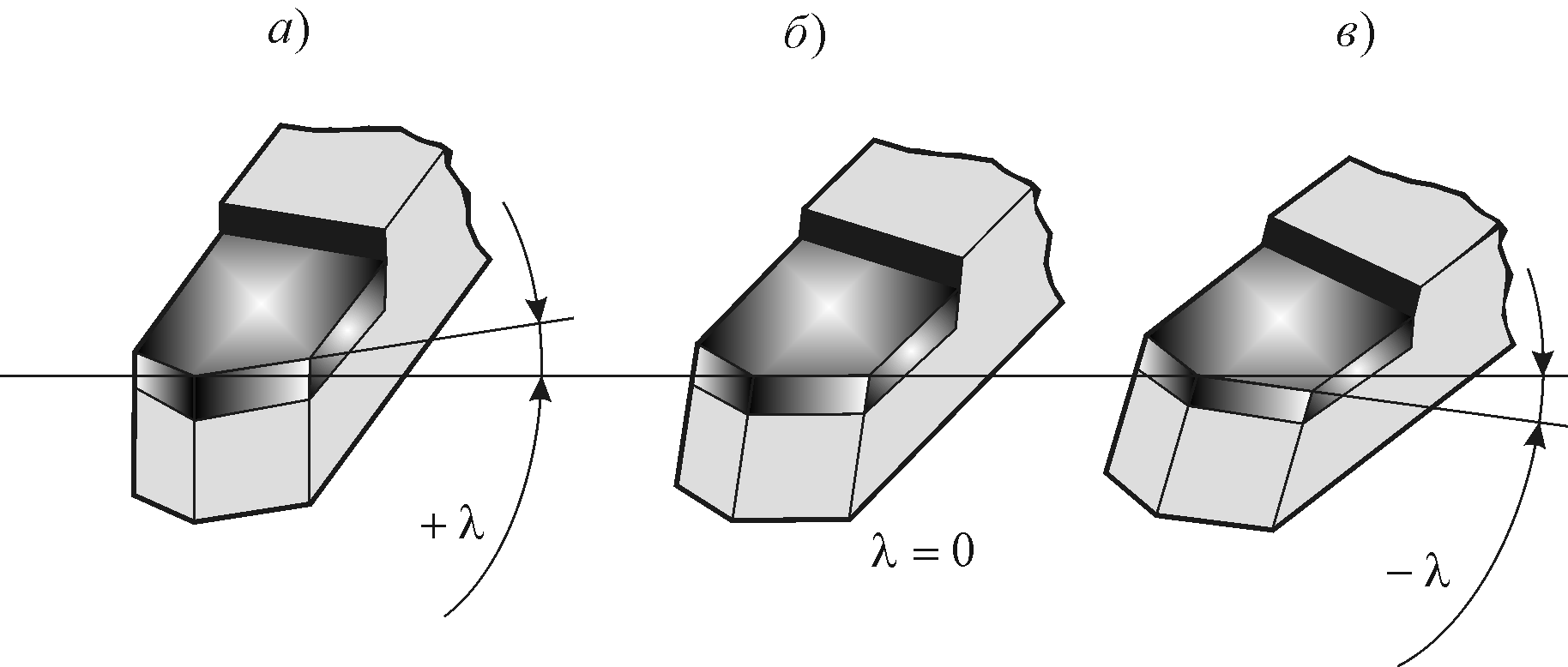
На рисунке 1.12 показан угол со стороны главной задней поверхности.
|
Рисунок 1.12 – Угол со стороны главной задней поверхности |
Угол наклона главной режущей кромки может быть положительным (рисунок 1.12, а), равным нулю (рисунок 1.12, б), отрицательным (рисунок 1.12, в).
При положительном угле - вершина резца занимает низшее положение на главной режущей кромке, при отрицательном угле - вершина резца занимает высшее положение на главной режущей кромке.

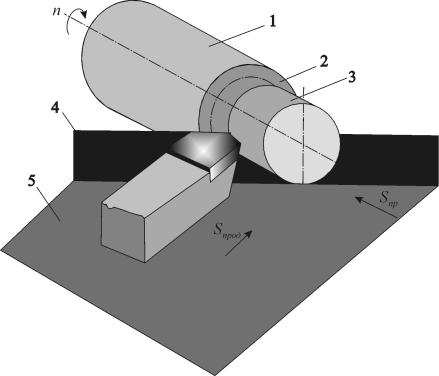 Рисунок
1.2 – Поверхности детали при точении
Рисунок
1.2 – Поверхности детали при точении 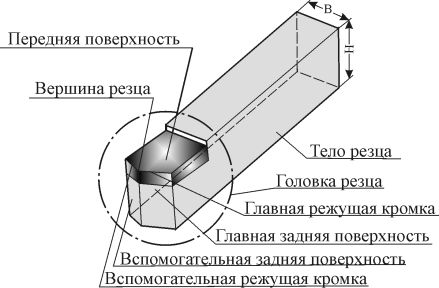









 Ри
Ри