ВВЕДЕНИЕ

Методические указания предназначены для решения задач теплообмена по 8 темам дисциплины " Теоретические основы теплотехники".

В разд. 1 – 4 рассматриваются методики определения распределения температурных полей в процессах теплопроводности тел с внутренними источ-никами тепла, нагрева плоских тел в условиях нестационарной теплопровод-ности, передачи теплоты через оребренные поверхности плоской и цилиндри-ческой стенок. Методики исходят из закона теплопроводности Фурье при реше-нии дифференциальных уравнений с граничными условиями третьего рода.

В разд. 5 – 7 описываются методики расчета конвективного теплообмена при обтекании греющей (нагреваемой) средой плоской поверхности и в случаях фазного преобразования среды (кипение воды и конденсация пара). Вследствие сложности аналитического описания этих процессов теплообмена использова-ны известные инженерные методы расчета, исходящие из критериальных урав-нений, полученных при экспериментальном исследовании подобных физичес-ких явлений. Даны рекомендации оценки влияния на интенсивность теплообме-на основных факторов, оценивающих состояние поверхности и изменение фи-зических характеристик жидкости или газа.

В разд. 8 рассмотрено решение задачи лучистого теплообмена при коак-сиальном расположении цилиндрических тел, исходящих из основных зако-номерностей теплообмена излучением.

В приложениях приведены данные параметров и физических характерис-тик воды, водяного пара, а также сухого воздуха. Промежуточные значения параметров и физических характеристик сред в пределах узкого интервала из-менения следует определять методом линейной интерполяции.

1. Теплопроводность цилиндрической стенки при наличии внутреннего источника теплоты

При прохождении электрического тока по цилиндрическому элементу ка­лорифера за единицу времени в единицу объема выделяется теплота , . Снаружи цилиндрическая трубка охлаждается воздухом. Принимая полый ци­линдр бесконечной длины, для стационарного теплообмена уравнение сохра­нения энергии в цилиндрических координатах запишем в следующем виде:

^. (1)

Граничные условия:

на оси цилиндра и его внутренней поверхности –

(2)

на внешней поверхности –

. (3)

Общее решение уравнения (1) имеет вид:

. (4)

С учетом граничных условий и определения постоянных интегрирования с₁ и с₂ частное решение принимает вид:

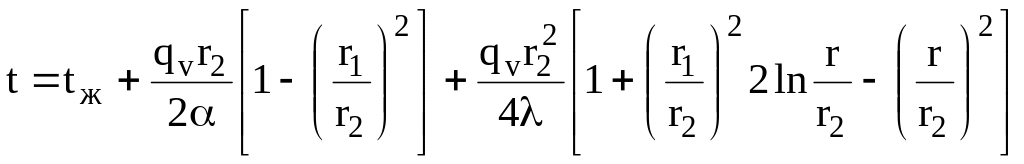. (5)

Полученное выражение (5) температурного поля позволяет определить температуру в любой точке трубчатого сечения элемента:

на внешней поверхности (при r = r₂)

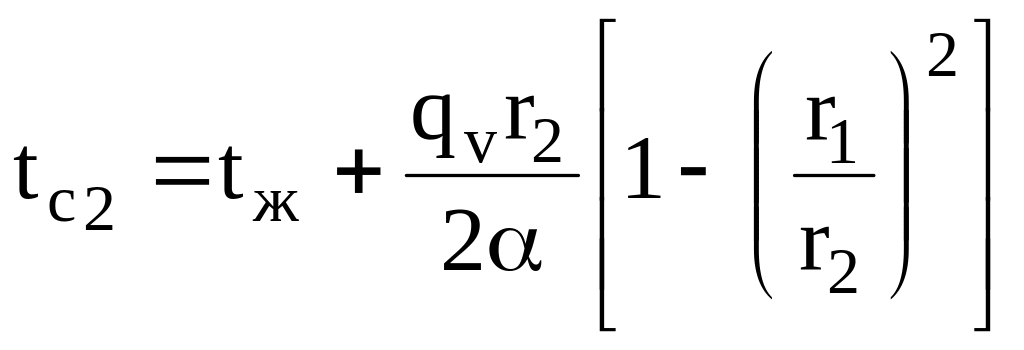; (6)

на внутренней поверхности (при r = r₁)

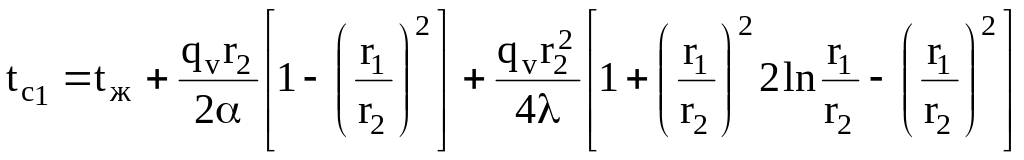. (7)

Плотность теплового потока с единицы теплоотдающей поверхности оп­ределится по формуле:

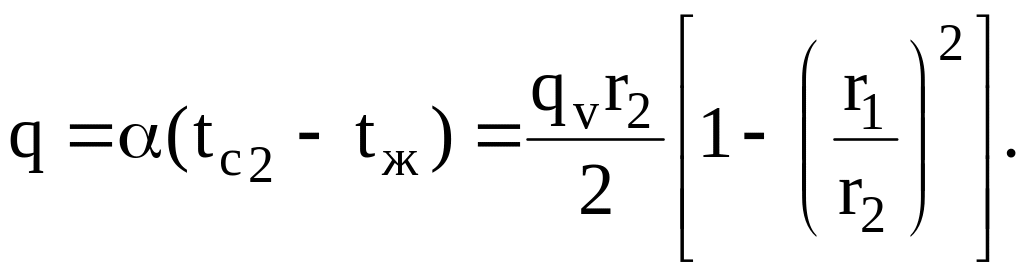(8)

Электрическое сопротивление одного метра трубки

(9)

где – площадь сечения трубки.

Количество выделяющегося тепла

, (10)

тогда поверхностная плотность теплового потока

, (11)

где – площадь внешней поверхности трубки, а теплопроизводитель- ность внутреннего источника теплоты, ,

(12)

где – объем тела элемента.

Коэффициент теплоотдачи при конвективном теплообмене элемента кало­рифера, располагаемого в глубинных рядах (начиная с третьего) кори­дорного или шахматного пучка труб для смешанного режима движения теп­лоносителя можно определить, воспользовавшись рекомен­дациями [1]:

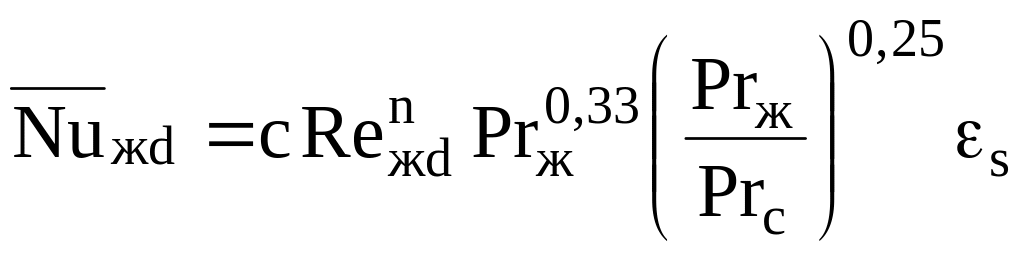, (13)

где для коридорных пучков с = 0,26, n = 0,65; для шахматных c = 0,41, n = 0,60;

– поправочный коэффициент, учитывающий влияние относительных шагов расположения труб в пучке.

Для глубинных рядов коридорного пучка

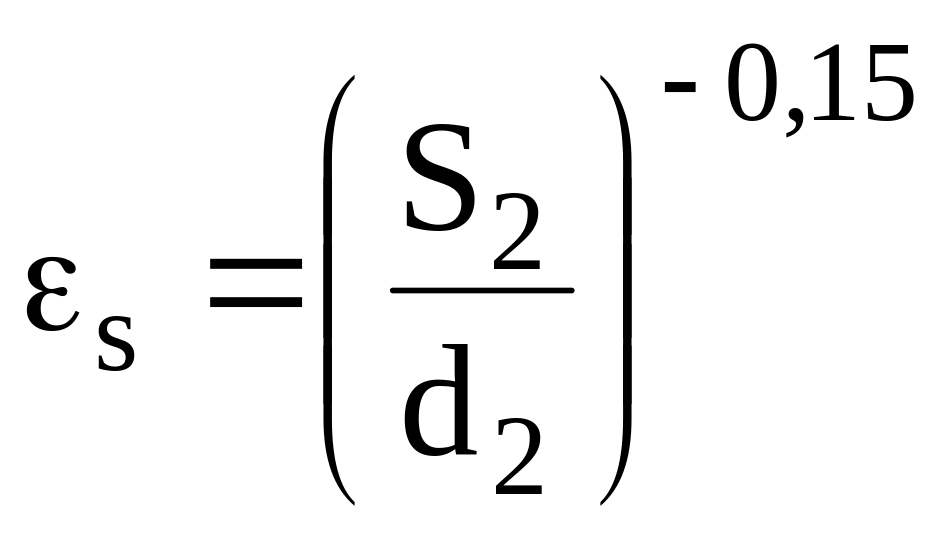, (14)

для шахматного –

при 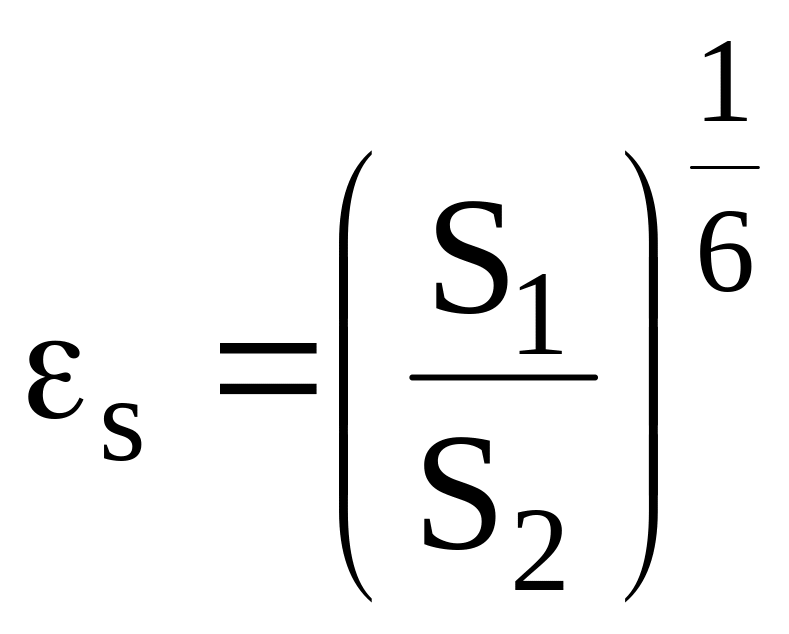; (15)

при . (16)

За определяющий размер и температуру следует принимать внешний диаметр трубки и температуру среды. Число Pr_c принимается по темпе­ратуре стенки трубки.

Дополнительные сведения по расчету коэффициента вне указанных пределов измене­ния Re_жd можно найти в [2].

При исследовании теплообмена элемента калорифера следует опреде­лить изменение температуры по сечению, построить и проанализировать графические зависимости ; ; .