Волновая теория передачи по световодам.

Она включает рассмотрение процесса распространения света как разновидности электромагнитных волн.

М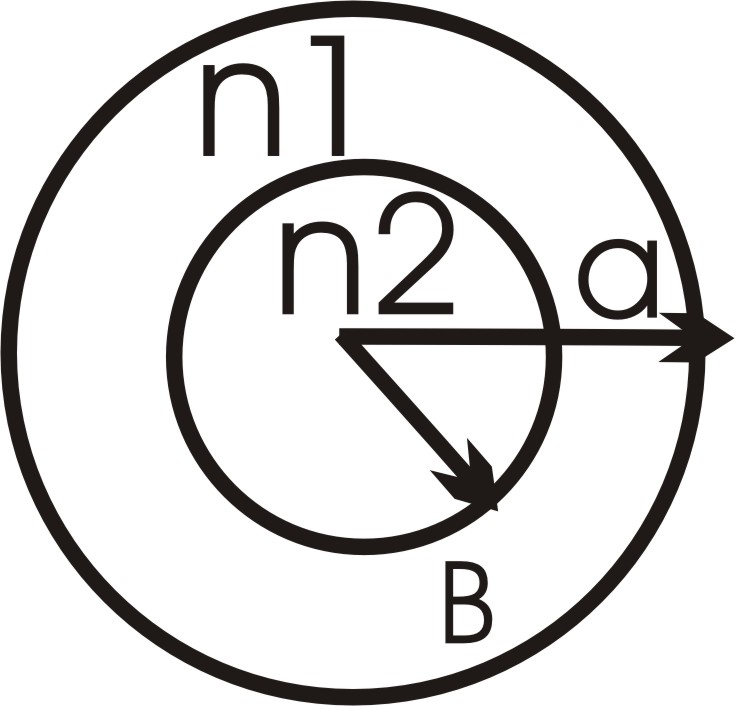 атематически решения осуществляется на основе уравнений Максвелла с использованием цилиндрических функций.

Для описания полей в сердечнике (0<r<a) и в оболочке (0<r<b) необходимо использовать различные функции.

Исходя из физической сущности процессов, функции внутри сердечника при r=0 должны быть конечными, а в оболочке должны пронизывать спадающее поле. Используем цилиндрическую систему координат.

Поперечные составляющие Электромагнитного поля могут быть выражены через продольные и

1. Для сердечника имеем систему уравнений

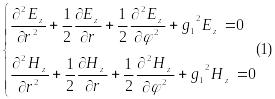
где поперечный коэффициент распространения в сердечнике световода

• - коэффициент распространения в световоде .

• - волновое число среды с коэффициент преломления

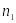
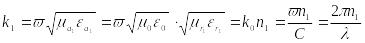
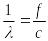
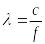
Решение уравнений (1) ищется через цилиндрические функции первого рода - функции Бесселя , имеющие конечные значения при r=0

Поэтому для r<a можно написать

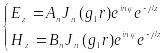
и - постоянные интегрирования.

Поперечные составляющие через продольные

б) для оболочки система уравнений имеет вид

-поперечный коэффициент распространения в оболочке световода

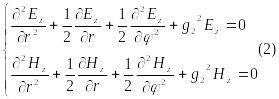
- поперечный коэффициент распространения в световоде

- волновое число сферы с коэффициентом преломления

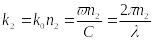
Для решения данных уравнений, исходя из условий, что при …. поле должно стремиться к нулю, следует, что при цилиндрические функции 3-го рода – функции Гангеля.

Cn и Dn постоянные интегрирования

Поперечные составляющие в оболочке:

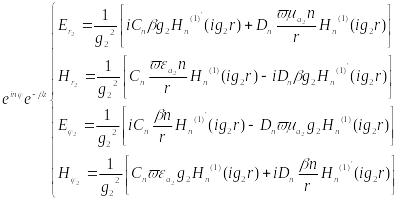
могут быть определены на основании граничных условий:

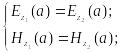
Условия равенства тангенциальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердцевина-оболочка:

Подставив в уравнения (1) и (2) найденные постоянные интегрирования, мы получим следующие трансцендентные уравнения:

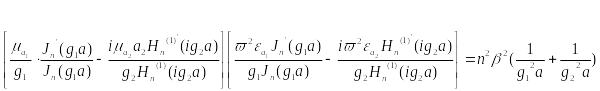
Полученное уравнение дает возможность определить структуру поля в сердечнике и оболочке волоконного световода.

В общем случае уравнение имеет ряд решении, каждому из которых существует определенная структура поля, называемая типом волны или модой.

В световодах могут существовать два типа волн:

симметричные

И несимметричные дипольные

n – число изменений поля по диаметру (порядок функции)

m - число изменений поля по диаметру (номер корня)

С имметричные волны электрические и магнитные имеют круговую симметричную (n=0).

Раздельное существование и в световоде невозможно. Они существуют совместно, т.е. имеются продольные составляющие Е и Н. Эти волны называются гибридными.

HEmn – если напоминают волны Н.

EHnm - если напоминают волны Е

согласно волновой теории по световоду распространяется ограниченное число волн.

Обычно режим работы световода характеризуется параметром . Этот параметр называется нормированной частотой.

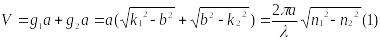
Рассмотрим и

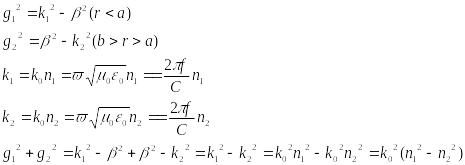
Для определения f кр. Надо принять g₂=0 - это условие соответствует углу полного внутреннего отражения. В данном случае преломленная волна полностью отсутствует, есть только падающая и отраженная.

В данном случае имеем:

умножим числитель и знаменатель на «a»

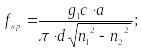
соответственно

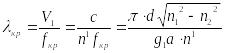, где

Сравнивая эту формулу с ранее полученной методом геометрической оптимизации, видна ее полная тождественность.

Разница лишь в параметре , который характеризует тип волны.

Анализируя выражение можно сказать, что чем больше d и разность , тем

больше и меньше . при равенстве n₁ и n₂ передача по такому световоду невозможна.

Это имеет свое логическое обоснование: при отсутствии границы световод перестает действовать как направляющая система.

Для определения критических частот различных типов волн рассмотрим корни ранее полученных бесселевых функций для симметричных и несимметричных волн.

Эти равенства дают бесконечное число корней, значения которых приведены в табл. 5.11.

Корни бесселевых функций могут быть представлены в следующем виде. При частоте отсечки , имеем равенство: , тогда

Сравнивая (2) с (1), видим что они индентичны, только вместо λ взято λкр Т.о. каждая мода имеет нормированную частоту, которая определяет область ее существования.

При такой трактовке табл. 5.11 содержит в колонке «значение корня» нормированные частоты для волн, тип которых указан в правой колонке таблицы, а индекс nm составлен из чисел левого столбца и верхней строки, соответствующей клетки, в которой находится данная величина , каждой соответствует

При имеем , т.е. частота меньше критической и волна по сердцевине волокна не распространяется, т.е. не существует.

При волна распространяется. Для волны , т.е. она может распространяться при любом диаметре и любой частоте.

Анализ табл. 5.11:

Условие можно выполнить, уменьшая либо разность и , либо радиус сердечника. Для типичного случая ( =1,5 и =1,49) U 0.6 и, следовательно, max значения 2a=6.8мкм при 12,8мкм и λ= 1.6 мкм.

Волна используется при передаче по одномодовым световодам. Здесь магнитные линии повторяют электрические см. рис. 5.51

Зависимость появления новых мод с ростом V иллюстрируется в таблице 5.12.

Общее число передаваемых мод в световодах может быть определено по формулам

для

для градиентного профиля

меньшие имеют в 2 раза меньше мод

для уменьшения числа мод надо уменьшить и

На рис. 5.52 показана одномодовая и многомодовая схемы передачи по световодам.

Справа волновая теория

Слева – лучевая

В общем случае в волновом световоде могут существовать 3 типа волн:

Направляемые, излучаемые, и вытекаемые

Существование того или иного типа

Связано с апертурой и соотношением углов падения

И полного внутреннего отражения