1.Загальний вигляд теоретичного та емпіричного рівнянь парної лінійної регресії, їх складові елементи. Причини, які спонукають появу випадкової складової ε в регресійних моделях. Етапи побудови економетричної моделі.

Теоретичне лінійне рівняння регресії в загальному випадку являє собою лінійну функціональну залежність між умовним ма­тематичним сподіванням залежної змінної У, M(Y/X)=xi.та пояснювальною змінною (регресором) X: M(Y/X=Xi)=β₀+β₁x₁.В загальному вигляді теоретична лінійна модель парної ре­гресії записується так:y_i=β₀+β₁x_i+ ε_i, i=1,n. Емпірична лінійна модель парної регресії має вигляд: :y_iⁿ=β₀ⁿ+β₁ⁿx_i+e_i, i= . Стохастичну складову ε економетричної моделі називають помилкою (залишком,збуренням, відхиленням).Причинами виникнення випадкового елемента ε можуть бути:1)Будь-яка регресійна модель є певною мірою спрощенням реальної ситуації, яка насправді являє собою складне переплетіння різних факторів, багато з яких фізично не можна врахувати в моделі.2)Неправильно вибрана форма функціональної залежності між змінними в моделі.3)Агрегування змінних4)Помилки вимірювання, які можуть бути допущенні під час аналізу й обробки статистичних даних.5)Обмеженість статистичних даних проявляється в тому, що більшості моделі виражаються переважно неперервними функціями, але при цьому використовується набір даних, що має дискретну структуру.6)Непередбаченість людського фактора, може бути одним із головних проявів відхилень незалежної змінної в модельованих значеннях. Побудова будь-якої економетричної моделі здійснюється як послідовність певних кроків. Крок 1. Знайомство з економічною теорією, висунення гіпотези взаємозв’язку. Чітка постановка задачі.Крок 2. Специфікація моделі. Використовуючи всі ті форми функцій, які можуть бути застосовані для вивчення взаємозв’язків, необхідно сформулювати теоретичні уявлення і прийняті гіпотези у вигляді математичних рівнянь.Крок 3. Формування масивів вихідної інформації згідно з метою та завданнями дослідження.Крок 4. Оцінка параметрів економетричної моделі методом найменших квадратів, що дає змогу проаналізувати залишки і відповісти на запитання: чи не суперечить специфікація моделі передумовам “класичної” моделі лінійної регресії? Крок 5. Якщо деякі передумови моделі не виконуються, то для продовження аналізу треба замінювати специфікацію або застосовувати інші методи оцінювання параметрів.Крок 6. Проведення аналізу вірогідності моделі та визначення прогнозу за побудованою моделлю.

2.Яка модель відноситься до категорії економетричних? Що таке загальна модель? Лінійна модель? Як записується економетрична модель у загальному вигляді для фактичних даних та який її склад? Які змінні у моделі є незалежними? Чому вони називаються пояснювальними? Які змінні у моделі є залежними? Чому вони називаються пояснюваними?

Модель, що описує кореляційно-регресивний зв'язок між економічними показниками називається загальною, яка дійсна для всієї генеральної сукупності спостережень. Економетрична модель виступає як функція або система функцій, що описує зв'язок між вхідними та результативними показниками економічноїсистеми за допомогою методів математичної статистики. У загальному матричному вигляді економетрична модель для фактичних даних записується так:Y = AX + u, де А - матриця параметрів моделі розміром m*n (m - кількість незалежних змінних, n - число спостережень); Y - матриця значень залежної змінної; X - матриця незалежних змінних и -матриця випадкової складової. У лінійній економетричні моделі має місце лінійний зв'язок між змінними, що характеризують розглядаємій економічний процес чи явище. Незалежні фактичні змінні X (пояснювальні змінні) найчастіше бувають детермінованими і вони є наперед заданими змінними, або вхідними показниками для розглядаємої економічної системи. З огляду того, що залежні фактичні змінні Y (пояснювані змінні), які є результативними показниками, залежать від випадкової складової и, то вони також є стохастичними (випадковими). Звідси і економетрична модель є стохастичною.

3. Яка задача вирішується в регресійному аналізі?Яка задача вирішується в кореляційному аналізі?Які вимоги накладаються на застосування кореляційно-регресійного аналізу?Які етапи побудови економетричної моделі?Який вигляд має теоретична економетрична модель?

Задачею регресійного аналізу є встановлення виду залежності між змінними та вивчення залежності між ними. Основною задачею кореляційного аналізу є виявлення зв'язку між змінними та оцінка її тісноти та значимості. Але на застосування кореляційно-регресійного аналізу накладуються такі вимоги:необхідність достатньо великої сукупності спостережень;забезпечення однорідної сукупності спостережень;наявність нормального закону розподілення сукупності вивчаємих одиниць, на якому побудовані всі положення кореляційно-регресійного аналізу. Побудова будь-якої економетричної моделі базується на використанні таких специфічних послідовних етапів, загальний вид яких розглянутий у п. 1.6:Етап 1. Постановка задачі.

Етап 2. Специфікація моделі, яка полягає у встановлені функції або системи функцій, що використовуються для побудови моделі з ймовірними характеристиками.Етап 3. Формування вхідної інформації згідно з метою дослідження.Етап 4. Оцінка параметрів моделі регресії за допомогою методу найменших квадратів.Етап 5. Перевірка передумов виконання вимог до моделі; у разі порушення розглянутих вимог треба змінити специфікацію або застосувати інші методи оцінювання параметрів.Етап 6. Проведення аналізу достовірності моделі та прогнозу за побудованою моделлю.Теоретична (“канонічна”) загальна лінійна економетрична модель може бути специфікована в наступній форм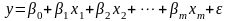і : ,де y – залежна (пояснювана) змінна моделі, x₁, x₂, … , x_m – незалежні (пояснюючі) змінні моделі або фактори, β₀, β₁, …. , β_m – параметри моделі, ε – стохастична складова моделі, m – кількість пояснюючих змінних моделі.

4. Що називається специфікацією економетричної моделі?Що приводить до помилок специфікації?

Специфікацію моделі називають її аналітичну форму, яка складається з певного виду вибраної функції чи системи функцій для змінних. До помилок специфікації приводять:відсутність у моделі основної пояснювальної (незалежної) змінної, що призводять до зміщення оцінок параметрів і може привести до хибних висновків щодо значень параметрів;введення в модель пояснювальної змінної, яка не є істотною для вимірюваного зв'язку, що може привести до неправильно встановленого кількісного зв'язку між змінними; використання невідповідних аналітичних форм вибраних функцій для моделі, що як і при першій помилці специфікації може привести до зміщення оцінок параметрів моделі.

5. За яких умов можливо використання 1МНК?При виконанні якої умови застосування 1МНК має місце гомоскедастичність?При порушенні якої умови застосування 1МНК має місце мультиколінеарність? До яких наслідків вона приводить?

Сутність методу полягає у знаходженні таких значень матриці параметрів А моделі загального вигляду Y = AX + u, при яких сума квадратів залишків и була б мінімальною, Тоді для фактичних значень залежних змінних У моделі теоретичні(розрахункові) значення змінних У будуть представлені у вигляді У = АХ. Наявність сталої (постійної) дисперсії залишків називається гомоскедастичністю. Ця властивість може виконуватись лише тоді, коли залишки и є помилками вимірювання. Якщо незалежні змінні пов'язані між собою, то це явище називають мультиколінеарністю і воно є небажаним, так як робить оцінку параметрів за допомогою 1МНК ненадійною чутливою до вибраної специфікації моделі.

6. Між якими змінними встановлює зв'язок рівняння парної регресії? Між якими змінними встановлює зв'язок рівняння множинної регресії? Які класи функцій в економетричній практиці описують взаємозв'язок між змінними у рівняннях регресії? Записати рівняння парної та множинної регресії при лінійній залежності між змінними, пояснити їх склад.

В регресійному аналізі розрізняють рівняння парної (простої) та множинної(багатофакторної) регресії. Коли зв'язок із залежною змінною у здійснюється з одним видом незалежних змінних х, то рівняння регресії є найпростішим і має назву рівняння парної регресії (проста модель). Якщо залежна змінна у пов'язана з декількома видами незалежних змінних Ху(j=1...т), то така залежність має назву рівняння множинної регресії.З досвіду економетричних досліджень, а також на підставі якісного теоретичного аналізу взаємозв’язків між економічними показниками можна навести клас функцій, які можуть описувати ці взаємозв’язки: лінійна функція; степенева функція;гіпербола;квадратична функція. Серед наведених щойно видів функцій три останні є нелінійними. Але за допомогою перетворення залежної і незалежних змінних ці функції можна звести до лінійних. Отже, всі записані функції можуть бути реалізовані на практиці як лінійні.Лінійна залежність: парна регресія: y=a₀+a₁x; множинна регресія: y=a₀+a₁x₁+a₂x₂+…a_nx_n.

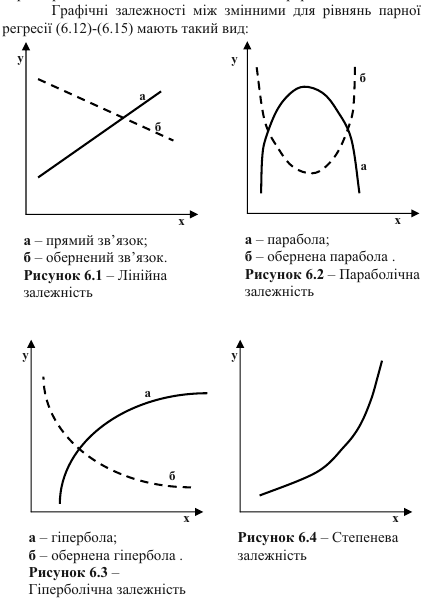
7. Записати рівняння парної та множинної регресії при параболічній залежності між змінними, пояснити їх склад. Записати рівняння парної та множинної регресії при гіперболічній залежності між змінними, пояснити їх склад. Записати рівняння парної та множинної регресії при степеної залежності між змінними, пояснити їх склад. Показати на графіку розповсюджені в економіці залежності між змінними.

Параболічна залежність: Парна регресія: y=a₀+a₁x², множинна регресія: y=a₀+a₁x₁²+a₂x₂²+…+a_mx_m².

Гіперболічна залежність: Парна регресія: y=a₀+a₁*1/x, множинна регресія: y=a₀+a₁/x₁+a₂/x₂+…+a_m/x_m.

Степенева залежність: Парна регресія: y=a₀x^a1, множинна регресія: y=a₀x₁^a1x₂^a2…x_m^am