Автомат Мили

В автомате Мили (англ. Mealy machine) функция выходов   определяет значение выходного символа по классической схеме абстрактного автомата. Математическая модель автомата Мили и схема рекуррентных соотношений не отличаются от математической модели и схемы рекуррентных соотношений абстрактного автомата. Таким образом, можно дать следующее определение:

Конечным детерминированным автоматом типа Мили называется совокупность пяти объектов

,

где S, X и Y — конечные непустые множества, а   и   — отображения вида:

 и 

со связью элементов множеств S, X и Y в абстрактном времени T = {0, 1, 2, …} уравнениями:

(Отображения   и   получили названия, соответственно функции переходов и функции выходов автомата A).

Особенностью автомата Мили является то, что функция выходов является двухаргументной и символ в выходном канале y(t) обнаруживается только при наличии символа во входном канале x(t).

Автомат Мура

Зависимость выходного сигнала только от состояния представлена в автоматах типа Мура (англ. Moore machine). В автомате Мура функция выходов определяет значение выходного символа только по одному аргументу — состоянию автомата. Эту функцию называют также функцией меток, так как она каждому состоянию автомата ставит метку на выходе.

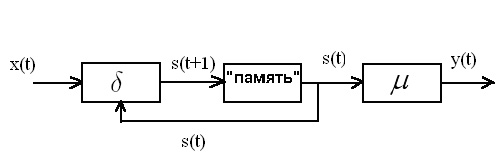
Функциональная схема автомата Мура

Конечным детерминированным автоматом типа Мура называется совокупность пяти объектов: 

где S, X, Y и δ — соответствуют определению автомата типа Мили, а μ является отображением вида: μ : S → Y,

с зависимостью состояний и выходных сигналов во времени уравнением:

. Особенностью автомата Мура является то, что символ y(t) в выходном канале существует все время, пока автомат находится в состоянии s(t).

Для любого автомата Мура существует автомат Мили, реализующий ту же самую функцию. И наоборот: для любого автомата Мили существует соответствующий автомат Мура.

6. Реализация секвенциальной логики на Verilog

В рамках секвенциальной логики выходное значение зависит не только от текущего входного воздействия, но и от предыстории функционирования цифрового устройства. Другими словами, секвенциальная логика предполагает наличие памяти, которая в комбинационной логике не предусмотрена.

Пример: Автомат Мили

Автомат Мили (англ. Mealy machine) — конечный автомат, выходная последовательность которого (в отличие от автомата Мура) зависит от состояния автомата и входных сигналов. Это означает, что в графе состояний каждому ребру соответствует некоторое значение (выходной символ). В вершины графа автомата Мили записываются выходящие сигналы, а дугам графа приписывают условие перехода из одного состояния в другое, а также входящие сигналы. Автомат Мили можно описать пятеркой (Q,X,Y,f,g), где Q - множество состояний автомата, X - множество входных символов, Y - множество выходных символов, q=f(Q,X) - функция состояний, y=g(Q,Y) - функция выходных символов. Кодировка автомата Мили: Вершина (операторная или логическая), стоящая после вершины "Начало", а также вход вершины "Конец" помечается символом S₁, вершины, стоящие после операторных помечаются символом S_n (n=2,3..).

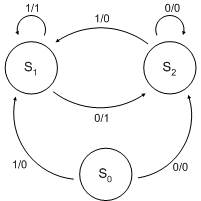
По способу формирования функций выходов выделяют автоматы Мили и Мура.