Логические функции (1,2,3 выводные). Законы де Моргана.
Нульарные функции
При n = 0 количество булевых функций сводится к двум 220 = 21 = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица. Таблица значений и названий нульарных булевых функций:
|
Значение |
Обозначение |
Название |
|
0 |
F0,0 = 0 |
тождественный ноль |
|
1 |
F0,1 = 1 |
тождественная единица, тавтология |
Унарные функции
При n = 1 число булевых функций равно 221 = 22 = 4. Определение этих функций содержится в следующей таблице.
x0=x |
1 |
0 |
Обозначение |
Название |
0 |
0 |
0 |
F1,0 = 0 |
тождественный ноль |
1 |
0 |
1 |
F1,1 = x = ¬x = x' = NOT(x) |
отрицание, логическое "НЕТ", "НЕ", "НИ", инвертор, SWAP (обмен) |
2 |
1 |
0 |
F1,2 = x |
тождественная функция, логическое "ДА", повторитель |
3 |
1 |
1 |
F1,3 = 1 |
тождественная единица, тавтология |
Бинарные функции
При n = 2 число булевых функций равно 222 = 24 = 16.
x1=x |
1 |
1 |
0 |
0 |
|
|
x0=y |
1 |
0 |
1 |
0 |
Обозначение |
Название |
0 |
0 |
0 |
0 |
0 |
F2,0 = 0 |
тождественный ноль, детектор 0 |
1 |
0 |
0 |
0 |
1 |
F2,1 = x ↓ y = x NOR y = NOR(x,y) = x НЕ-ИЛИ y= НЕ-ИЛИ(x,y) |
стрелка Пи́рса, НЕ-ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, детектор 1 |
2 |
0 |
0 |
1 |
0 |
F2,2 = x ← y = x < y = x LT y = LT(x,y) |
инверсия обратной импликации, меньше, детектор 2 |
3 |
0 |
0 |
1 |
1 |
F2,3 = x = x' = ¬x = NOT1(x,y) = НЕ1(x,y) |
отрицание (негация, инверсия) первого операнда |
4 |
0 |
1 |
0 |
0 |
F2,4 = x → y = x > y = x GT y = GT(x,y) |
инверсия прямой импликации, больше, детектор 4 |
5 |
0 |
1 |
0 |
1 |
F2,5 = y = y' = ¬y = NOT2(x,y) = НЕ2(x,y) |
отрицание (негация, инверсия) второго операнда |
6 |
0 |
1 |
1 |
0 |
F2,6 = x ⊕ y = x XOR y = XOR(x,y) = x >< y = x<> y = x NE y = NE(x,y) |
сложение по модулю 2, исключающее «или», сумма Жегалкина[5], не равно |
7 |
0 |
1 |
1 |
1 |
F2,7 = x | y = x NAND y = NAND(x,y) = x НЕ-И y = НЕ-И(x,y) |
штрих Ше́ффера, НЕ-И, 2И-НЕ, антиконъюнкция, пунктир Чулкова |
8 |
1 |
0 |
0 |
0 |
F2,8 = x ∧ y = x · y = xy = x & y = x AND y = AND(x,y) = x И y = И(x,y) = min(x,y) |
конъюнкция, 2И, минимум, детектор 8 |
9 |
1 |
0 |
0 |
1 |
F2,9 = (x ≡ y) = x ~ y = x ↔ y = x EQV y = EQV(x,y) |
эквивалентность, равенство |
10 |
1 |
0 |
1 |
0 |
F2,10 = YES2(x,y) = ДА2(x,y) = y |
второй операнд |
11 |
1 |
0 |
1 |
1 |
F2,11 = x → y = x ⊃ y = x ≤ y = x LE y = LE(x,y) |
прямая (материальная) импликация (от первого аргумента ко второму), меньше или равно |
12 |
1 |
1 |
0 |
0 |
F2,12 = YES1(x,y) = ДА1(x,y) = x |
первый операнд |
13 |
1 |
1 |
0 |
1 |
F2,13 = x ← y = x ⊂ y = x ≥ y = x GE y = GE(x,y) |
обратная импликация (от второго аргумента к первому), больше или равно |
14 |
1 |
1 |
1 |
0 |
F2,14 = x ∨ y = x + y = x OR y = OR(x,y) = x ИЛИy = ИЛИ(x,y) = max(x,y) |
дизъюнкция, 2ИЛИ, максимум |
15 |
1 |
1 |
1 |
1 |
F2,15 = 1 |
тождественная единица, тавтология |
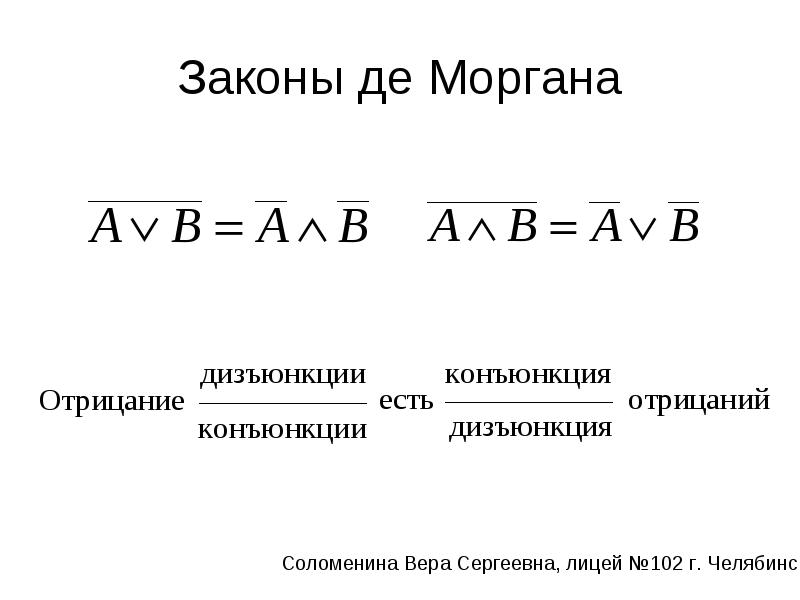
Законы де Мо́ргана (правила де Мо́ргана) — логические правила, связывающие пары дуальных логических операцийпри помощи логического отрицания. Открыты шотландским математиком Огастесом де Морганом.
