5.2 Изучаемая функция
Функция создания обобщенно-регрессионной НС
net=newgrnn(P, T, spread). Обобщенно-регрессионная НС является вариантом нейронной сети с радиальными базисными элементами. P – матрица входных векторов, T – матрица целевых векторов, spread – отклонение (по умолчанию 1.0). Сеть создается обученной.
5.3 Порядок выполнения работы
1. Пример решения задачи аппроксимации функции с использованием обобщенно-регрессионной НС.
>>P=[1 2 3 4 5 6 7 8 9 10]; % Входной вектор
>
>
T=[0.5 1 1.5 2 1.5 2 2.5 3 2.5 2]; % Целевой вектор
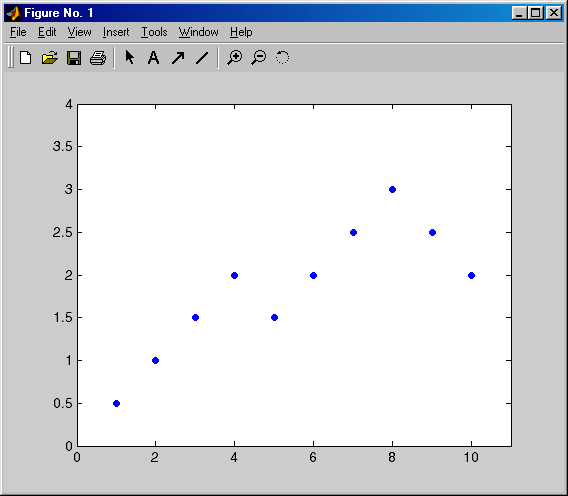
% Строим график опытных данных (см. рисунок 14)
>> plot(P,T, '.', 'markersize', 15);
>> hold on;
>> axis([0 11 0 4]); % Устанавливаем размерность осей по Х и У
% Создаем обобщенно-регрессионную НС
>> net=newgrnn(P,T, 0.6);
% Проверим качество
аппроксимации на графике Рисунок 14 – График исходных данных
(см. рисунок 15)
>> plot(P, sim(net,P),'*','markersize',15,'color',[1 0 0]);
% Построим аппроксимированную функцию в виде сплошной линии
(Предварительно закрыв окно графика) – см. рисунок 16.
>> plot(P,T,'.','markersize',15); hold on;
>> X=1:0.1:10;
Рисунок 15 – Исходные () и Рисунок 16 – График аппроксимации
вычисленные сетью (*) значения функции нейросетью
>> plot(X,sim(net,X),'color',[0 0 0]);
>> p=6.5; % Используем сеть для вычисления функции в новой точке
>> a=sim(net,p);
% Нанесем вычисленное значение на график (см. рисунок 16)
>> plot(p,a,'*','markersize',15,'color',[1 0 0])
2. Пример аппроксимации функции обычной двухслойной нейронной сетью, обучающейся по алгоритму обратного распространения ошибки.
Информацию об определении количества нейронов в скрытом слое см.:
Demos-Toolboxes-Neural Networks-Generalization
Используйте нижний ползунок для выбора коэффициента сложности функции.
Используйте верхний ползунок для определения количества нейронов в скрытом слое НС.
Нажмите на кнопку "Train" для обучения двухслойной (logsig-линейной) сети решению задачи аппроксимации на данных, показанных слева.
Создадим НС для решения задачи на данных примера 1.
Входной и целевой вектор такие же, как в предыдущем примере.
Создаем двухслойную сеть. Входной слой состоит из одного элемента, значение которого может изменяться в диапазоне от 0 до 10. Внутренний слой состоит из 10 нейронов с логистической сигмоидальной функцией активации, выходной слой состоит из одного нейрона с линейной функцией активации.
>
>
net = newff([0
10], [10 1], {'logsig' 'purelin'});
% Обучаем созданную НС
>> net= train(net,P,T);
TRAINLM, Epoch 0/100, MSE 6.93038/0, Gradient 45.3963/1e-010
TRAINLM, Epoch 7/100, MSE 2.9267e-026/0, Gradient 2.34925e-013/1e-010
TRAINLM, Minimum gradient reached, performance goal was not met.
% Нанесем опытные данные на график (см. рисунок 17)
>>plot(P,T,'.','markersize',15); hold on;
% Нанесем на график результат работы сети:
>>plot(P,sim(net,P),'*','markesize',15);
% Нанесем на график результат аппроксимации функции в виде сплошной линии:
>> plot(X,sim(net,X),'color',[0 0 0]); Рисунок 17 – Результат аппроксимации функции logsig-линейной нейросетью
Тапсырма Нейронную сеть для получения линии регрессии по опытным данным: