1.Многокомпонентное разделение в каскадах

10.1. Параметры и характеристики ступени

Основные параметры центрифуг

Параметры и уравнения ступени

Обогащение ступени

10.2. Параметры и уравнения каскада

Основные параметры

Уравнения каскада

Критерии эффективности

10.3. Квазиидеальные и R-каскады

Методика расчета

Свойства R-каскадов

Свойства квазиидеальных каскадов

10.4. Оптимальные каскады

Методика расчета и оптимизации

Свойства оптимальных каскадов

Сравнение с R-каскадами

Разделение смеси изотопов с примесями

10.5. Прямоугольные каскады

Особенности расчета и оптимизации

Свойства прямоугольных каскадов

Ограничения на концентрации изотопов

3. Параметры и характеристики ступени Основные параметры центрифуг

Будем считать, что изотопная смесь состоит из s компонентов (s>2). Процесс ее разделения в центрифуге характеризуется 4s основными параметрами:

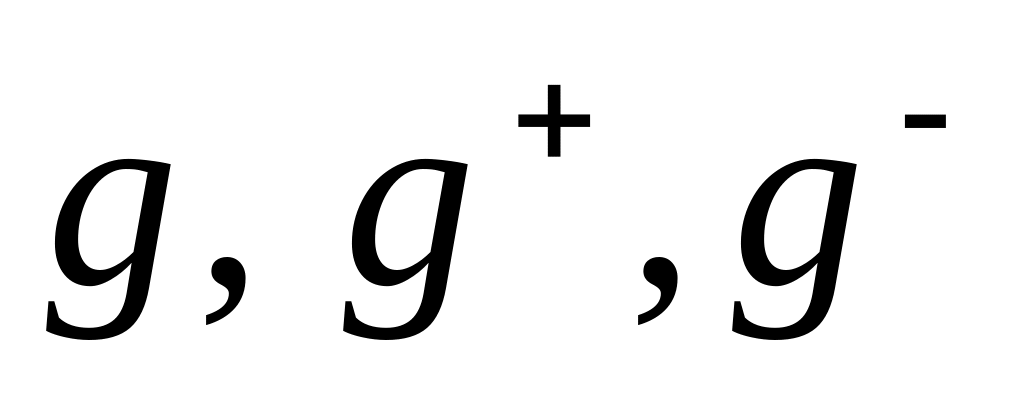• – потоки питания, отбора и отвала;

• – концентрации j-го компонента в питании, отборе и отвале, ;

• – полные коэффициенты разделения j-го компонента, ;

• – коэффициент деления потока.

Концентрации s-го компонента являются зависимыми и находятся вычитанием из единицы соответствующей суммы концентраций независимых j-х компонентов. Для удобства целесообразно принять, что компоненты пронумерованы в порядке возрастания их молекулярного веса и s-й компонент самый тяжелый.

Потоки и концентрации связаны s уравнениями баланса, которые в пренебрежении потерь в процессе разделения записываются в виде:

• для вещества

;

• для изотопных компонентов

, .

Полные коэффициенты разделения определяются как отношения относительных концентраций рассматриваемого изотопа и s-го компонента в отборе и отвале, т.е.

, .

При выборе тяжелого компонента в качестве s-го все коэффициенты . Их величина задается разделительными характеристиками

, , (10.1)

которые определяются в соответствии с разностью молекулярных масс j-го и s-го компонентов

, ,

где – полный коэффициент разделения на единицу разности масс.

С учетом формулы для коэффициента деления потока

основные 4s параметров связаны 3s–1 соотношениями. Поэтому независимыми являются s+1 параметров, в качестве которых можно принять . Остальные переменные рассчитываются из приведенных соотношений.

Параметры и уравнения ступени

Ступень ГЦ характеризуется аналогичной совокупностью параметров , связанных такими же уравнениями баланса, разделительными характеристиками и определениями.

При упрощающем допущении об одинаковости параметров центрифуг, концентрации соответствующих трасс ступени и центрифуг совпадают, а разделительные характеристики ступени соответствуют (10.1). Величина потока , входящая в (10.1), определяется по потоку питания и количеству центрифуг N, т.е. .

С учетом добавления и N в основные параметры их число составляет 4s+2 переменных. Они связаны 3s соотношениями. Поэтому количество независимых параметров ступени равно s+2. В качестве таких переменных целесообразно принять .