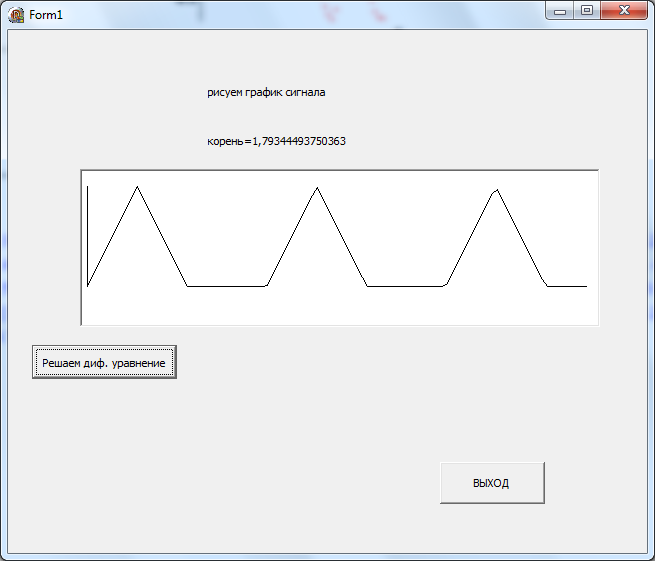
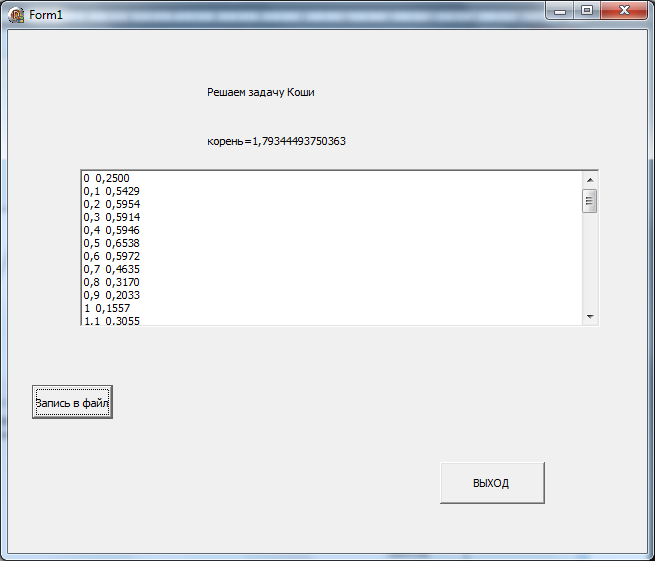
3.Скрины программы
4.Интегрирование дифференциального уравнения.
Сравнение с расчетами, выполненными в Turbo Delpi
> restart;
> with(linalg):with(plots):
pp:=(x,y)->[x,y];
Задаем модельный сигнал.
Это финитная
функция
единичной амплитуды, заданная на
единичном отрезке-носителе.
> fun:= proc(t) local z ;z:=piecewise(t<0,0,t<1/2,2*t,t<=1,2-2*t,0); evalf(z);end;
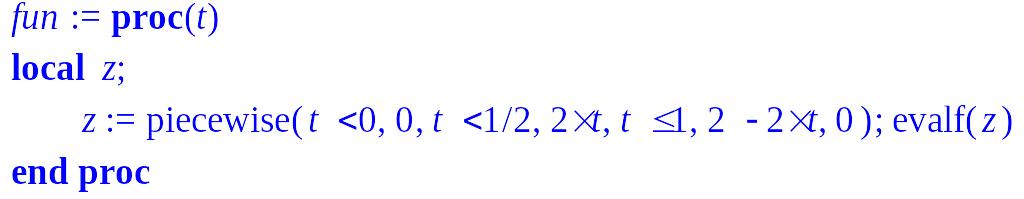
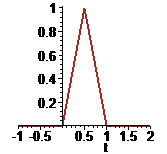
> plot(fun(t),t=-1..2,thickness=2,color=brown);
Полином
Первый положительный корень полинома определяет период T управляющего сигнала и коэффициент его усиления.
Величина
определяет длительность сигнала на
участке периода.
> p(x):=x^5-7*x-6;
> Koeff:=fsolve(p(x),x,0..2);
> T:=Koeff;
> tau:=1;
Процедура
Period(t,t0,tau,T,f)
строит периодическое продолжение
сигнала на всю действительную ось, где
T
- период,
- длительность сигнала f(t),
t0
-- начальный сдвиг (который можно
интерпретировать как запаздывание).
> Period:=proc(t,t0,tau,T,f) local x,z;
x:=evalf(t-t0-floor((t-t0)/T)*T);
z:=fun(x/tau);evalf(z);
end;
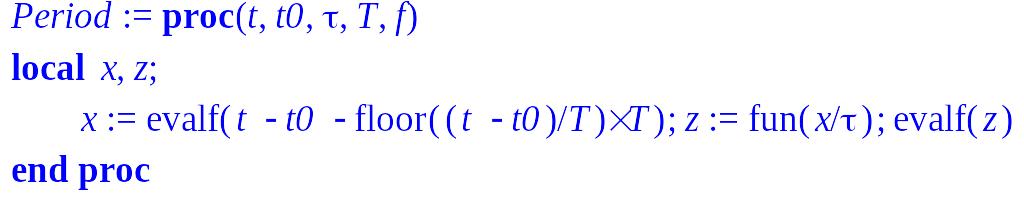
> plot(Period(x,0,tau,T,fun),x=-1..3,thickness=2,color=brown);
> #==================================================================
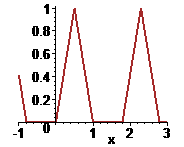
Решаем задачу интегрирования входного сигнала
Экспериментально так, чтобы выходной сигнал был близким к стационарному.
> Koc:=1;Nzac:=7;
> ur:=diff(U(t),t);
> F:=Nzac*(cos((4+Nzac/10)*t+U(t))+Koeff*Period(t,0,tau,T,f)-Koc*U(t));
> RK:=dsolve({ur=F,U(0)=0.25},U(t),type=numeric,output=listprocedure);
> fU:=subs(RK,U(t));
> T0:=5;Nt:=50;h:=T0/Nt;
> Tx:=array(0..Nt):U:=array(0..Nt):U_map:=array(0..Nt);
> for j from 0 to Nt do
x:=j*h;z:=fU(x);Tx[j]:=x;U[j]:=z;U_map[j]:=z;
#print(x,z);
od:
> RisU:=zip(pp,Tx,U):
> RU:=plot(RisU):
> display(RU);
> #====================================
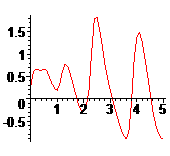
> RisU:=zip(pp,Tx,U):
> whattype([RisU]);
> RU0:=plot(RisU,style=point,symbol=cross):
> display(RU0);
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
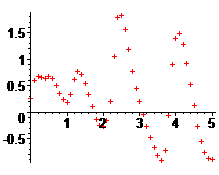
> fn:=`D:\\wrem\\сава.txt`;
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
> L:=readdata(fn,2);
Nstrok:=vectdim(L);
> U_n:=array(1..Nstrok);:
T_n:=array(1..Nstrok);
> for j from 1 to Nstrok do
T_n[j]:=L[j,1];
U_n[j]:=L[j,2];
#print(j,T_n[j],U_n[j]);
od:
> u1:=zip(pp,T_n,U_n):
> RU1:=plot(u1,style=point,symbol=cross,color=black):
> display(RU,RU1);
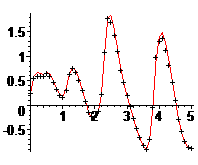
Сравнение результатов на одинаковых сетках
> printf("%s",` № t U_map U_pas разн \n`);
for k from 0 to Nt do t:=Tx[k]:del:=U_map[k]-U_n[k+1];
printf("% 3.0f % 6.2f % 8.4f % 8.4f % 8.4f \n",k,t,U_map[k],U_n[k+1],del):
end:;
№ t U_map U_pas разн
0 0.00 0.2500 0.2500 0.0000
1 0.10 0.5902 0.5429 0.0473
2 0.20 0.6686 0.5954 0.0732
3 0.30 0.6499 0.5914 0.0585
4 0.40 0.6294 0.5946 0.0348
5 0.50 0.6687 0.6538 0.0149
6 0.60 0.6394 0.5972 0.0422
7 0.70 0.5007 0.4635 0.0372
8 0.80 0.3497 0.3170 0.0327
9 0.90 0.2349 0.2033 0.0316
10 1.00 0.1875 0.1557 0.0318
11 1.10 0.3274 0.3055 0.0219
12 1.20 0.6228 0.6312 -0.0084
13 1.30 0.7754 0.7561 0.0193
14 1.40 0.7168 0.6719 0.0449
15 1.50 0.5445 0.5026 0.0419
16 1.60 0.3284 0.2978 0.0306
17 1.70 0.0986 0.0785 0.0201
18 1.80 -0.1312 -0.1435 0.0123
19 1.90 -0.2576 -0.2278 -0.0298
20 2.00 -0.2713 -0.2425 -0.0288
21 2.10 -0.1574 -0.1330 -0.0244
22 2.20 0.2102 0.2274 -0.0172
23 2.30 1.0514 1.0792 -0.0278
24 2.40 1.7867 1.7752 0.0115
25 2.50 1.8327 1.6999 0.1328
26 2.60 1.5513 1.4331 0.1182
27 2.70 1.1729 1.0939 0.0790
28 2.80 0.7690 0.7202 0.0488
29 2.90 0.4490 0.4590 -0.0100
30 3.00 0.1933 0.2083 -0.0150
31 3.10 -0.0450 -0.0339 -0.0111
32 3.20 -0.2728 -0.2650 -0.0078
33 3.30 -0.4857 -0.4793 -0.0064
34 3.40 -0.6743 -0.6681 -0.0062
35 3.50 -0.8233 -0.8163 -0.0070
36 3.60 -0.9029 -0.8972 -0.0057
37 3.70 -0.7202 -0.7068 -0.0134
38 3.80 -0.0655 -0.0543 -0.0112
39 3.90 0.9012 0.9790 -0.0778
40 4.00 1.3895 1.2936 0.0959
41 4.10 1.4820 1.3657 0.1163
42 4.20 1.2741 1.1247 0.1494
43 4.30 0.9205 0.8169 0.1036
44 4.40 0.5293 0.4679 0.0614
45 4.50 0.1288 0.0950 0.0338
46 4.60 -0.2709 -0.2909 0.0200
47 4.70 -0.5622 -0.5425 -0.0197
48 4.80 -0.7563 -0.7355 -0.0208
49 4.90 -0.8764 -0.8591 -0.0173
50 5.00 -0.8943 -0.8795 -0.0148