Уральский технический институт связи и информатики

Фгобу впо «СибГути»

Курсовая работа по дисциплине: «Языки программирования»

на тему: «Спектральный анализ сигналов».

Выполнил студен гр. РЕ-01

Кустышева Кристина

Проверил:

Кондратьев В.П.

Екатеринбург,2013 г.

Содержание

1.Задание для курсовой работы 3

2.Листинг программы 5

3.Скрины программы 10

4.Интегрирование дифференциального уравнения. Сравнение с

расчетами, выполненными в Turbo Delpi 14

5.Спектральный анализ программы средствами математического пакета MAPLE 20

Заключение 31

Библиография 32

1 Задание для курсовой работы

Написать программу на языке программирования Паскаль для решения следующей задачи (вариант задания индивидуальный). Результаты расчетов должны выводиться на экран и в файл. Оформление графиков и таблиц выполнять средствами математических пакетов (Maple, MathCad). Демонстрационный вариант программы подготовить в среде визуального программирования Delphi.

Проверить решение промежуточных задач средствами математических пакетов. Построить блок-схемы задачи и вспомогательных частей алгоритма. Оценить погрешность выполненных расчетов.

Напряжение U=U(t) на входе транзистора как функция времени описывается дифференциальным уравнением

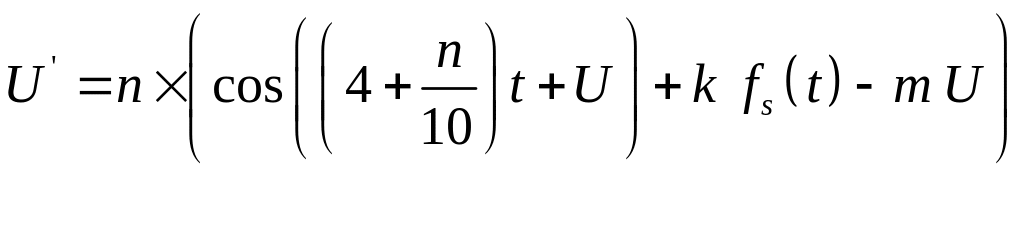
с начальными условиями (1), где n – последняя цифра номера зачетной книжки, k – коэффициент усиления (см. ниже), f_s(t) – периодический сигнал (рис. 1), m – коэффициент обратной связи.

Указания и пояснения.

1. Дифференциальное уравнение с заданными начальными условиями (задача Коши) решается методом Рунге-Кутта второго порядка с коррекцией (3) на отрезке [0;5] с шагом h=0.01.(в узлах t_j =jh, j=0,1,2…). Функция f_s(t) в правой части представляет собой регулирующий периодический (период Т) сигнал единичной амплитуды (рис 1, номер варианта n – последняя цифра номера зачетной книжки,). Результаты расчетов—таблица (t_j,U_j) и график функции U(t) (на экран и в файл).

2. Значение коэффициента усиления k в правой части дифференциального уравнения есть наименьший положительный корень полинома (2), который вычисляется одним из методов нахождения корней уравнения (метод касательных, метод Вегстейна).

3. Построить спектральные характеристики периодического сигнала f_s(t), заданного в аналоговой форме и в виде дискретного сигнала. Длительность сигнала равна 1, период T=k.

4. Период функции U(t) определить с помощью функции автокорреляции.

Курсовая работа выполняется в ЧЕТЫРЕ этапа.

1.Средствами математического пакета Maple решается задача спектрального анализа аналогового и дискретного периодического сигнала f_s(t). Сравниваются спектры амплитуд аналогового и дискретного представлений сигнала. (образец выполнения задания – файл вариант11.mws).

2.Создается проект в визуальной среде Delphi, решающий эту же задачу для дискретного сигнала, а результаты выполнения сравниваются визуально.

3.С помощью языка программирования системы Maple решается задача интегрирования дифференциального уравнения (задача Коши) методом (по варианту задания). Окончательные вычисления в программе зависят от результатов расчета программы в Delphi (следующий пункт). Образец выполнения задания – файл RUTTA.mws.

4.Создается проект в визуальной среде Delphi, решающий ту же задачу Коши, результаты расчета которой записываются в файл, который используется в предыдущем пункте. Выводятся графики результатов вычислений в Maple и Delphi и сравниваются между собой. Явные несовпадения свидетельствуют об ошибке в программе на Delphi.