Примерный вариант выполнения лабораторной работы на maple
Пример. Решить систему уравнений
x1+2*x2+3*x3=7,
x1-3*x2+2*x3=5,
x1+x2+x3=3.
Решение системы используя команду solve.
> restart;
> solve( {x1+2*x2+3*x3=7, x1-3*x2+2*x3=5, x1+x2+x3=3}, [x1, x2, x3]);
Решение линейной системы уравнений Ax=b.
Используя команду linsolve(A,b).
> restart;
> with(linalg):
> A := matrix(3,3, [1,2,3,1,-3,2,1,1,1]);
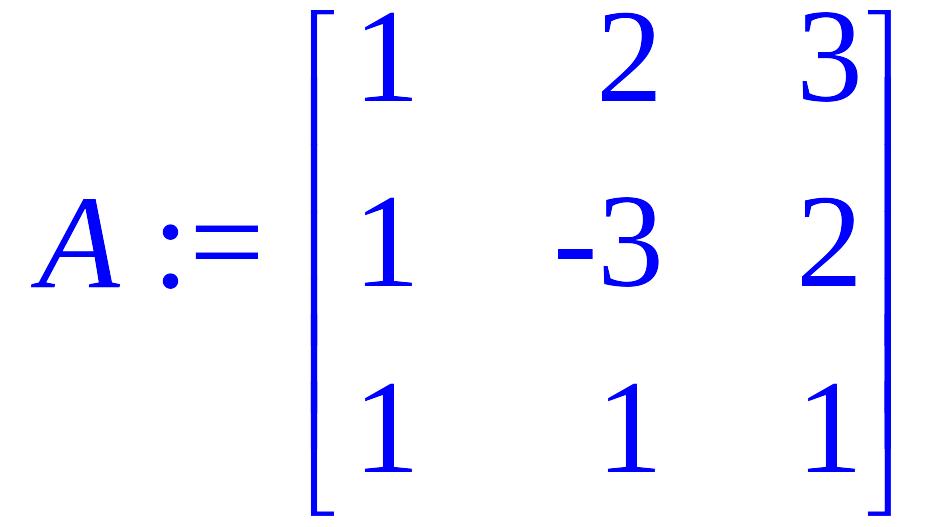
> b := vector( [7,5,3]);
> linsolve(A,b);
Решение линейной системы методом Гаусса
> restart;
> with(linalg):
> A := matrix(3,4, [1,2,3,7,1,-3,2,5,1,1,1,3]);
> gausselim(A,'r', 'd');
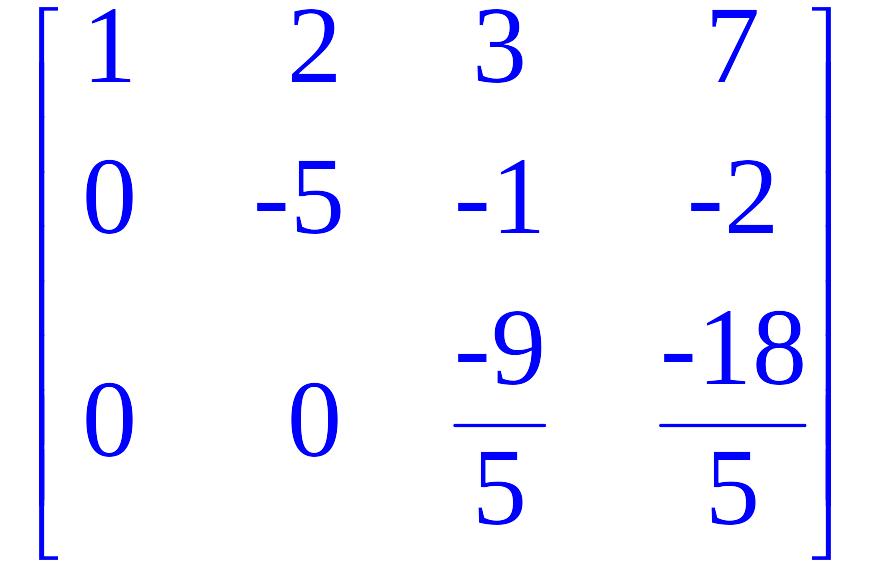
Из третей строчки получаем, что x3=2, подставляем во второе полученное x3 и находим x2=0, аналогично подставляя в первое равенство, получаем x1=1.
Вычисление решения системы по формуле x=C*b
C - матрица обратная к матрице A
> restart;
> with(linalg):
> A := matrix(3,3, [1,2,3,1,-3,2,1,1,1]);
> C:=inverse(A);
> b := vector( [7,5,3]);
> multiply(C,b);
Решение системы методом Крамера
> restart;
> with(linalg):
> B:=matrix(3,3, [1,2,3,1,-3,2,1,1,1]);
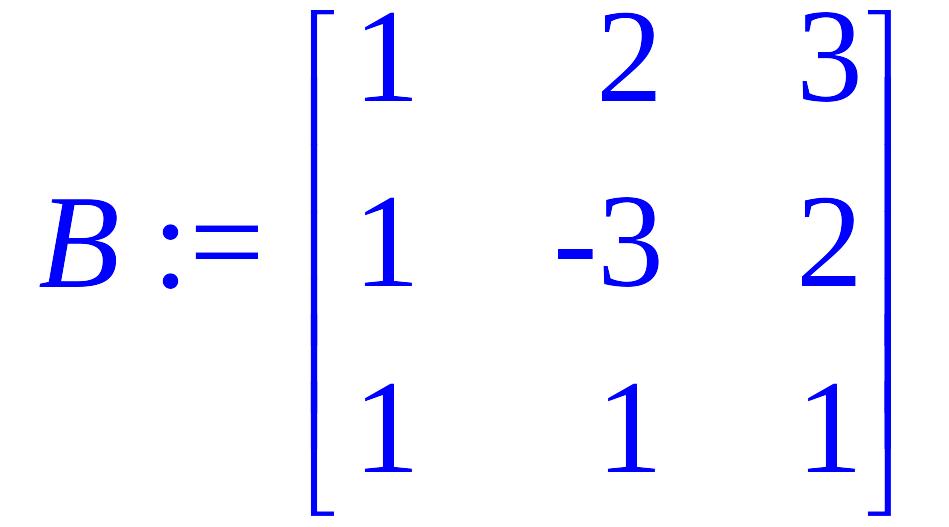
> det(B);
> B1:=matrix(3,3, [7,2,3,5,-3,2,3,1,1]);
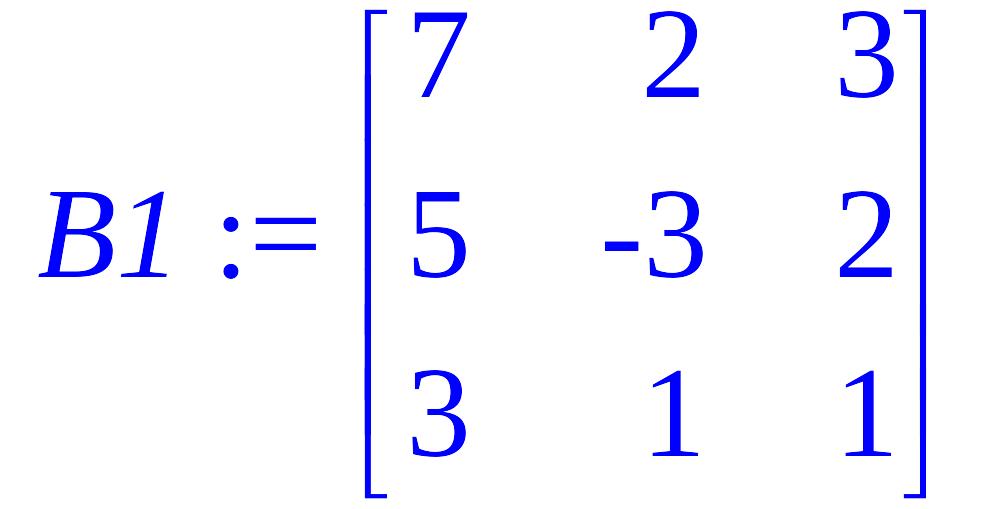
> det(B1);
> B2:=matrix(3,3, [1,7,3,1,5,2,1,3,1]);
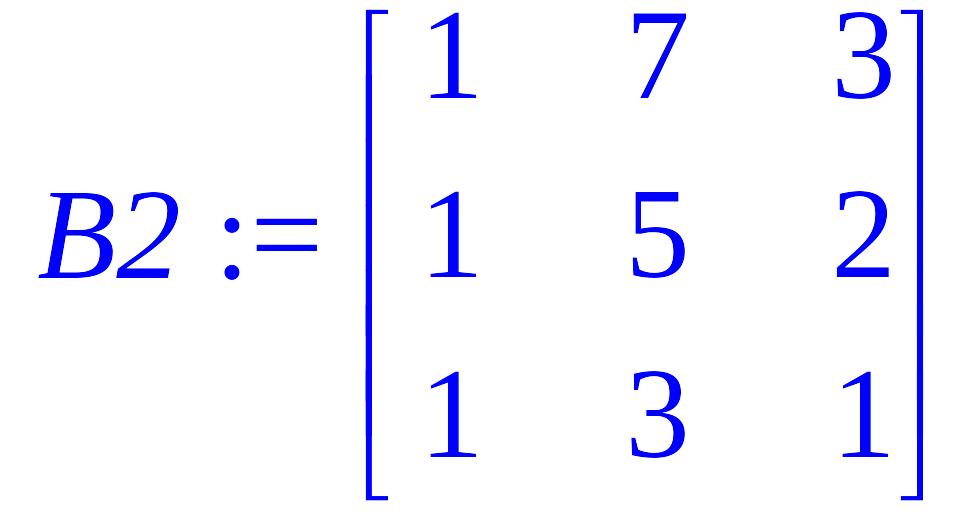
> det(B2);
> B3:=matrix(3,3, [1,2,7,1,-3,5,1,1,3]);
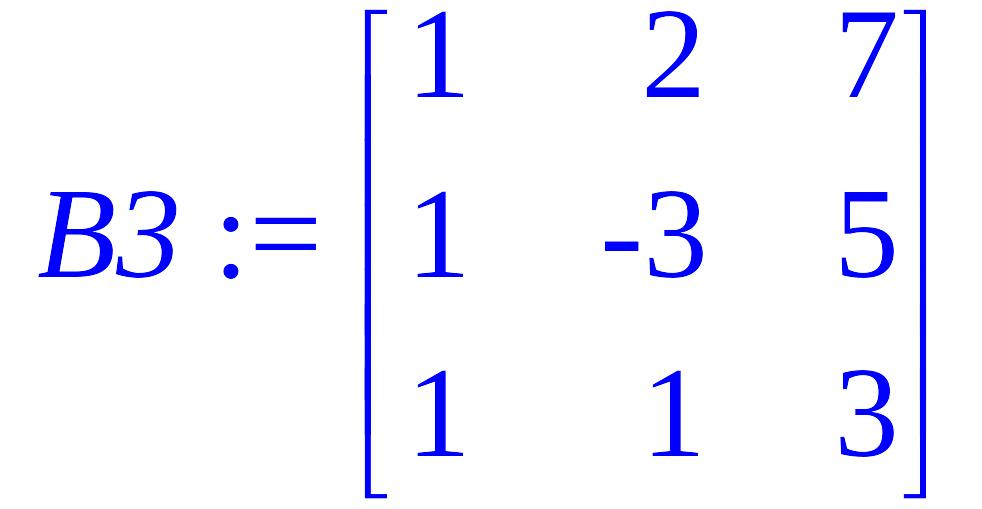
> det(B3);
> x1:=det(B1)/det(B); x2:=det(B2)/det(B); x3:=det(B3)/det(B);
> #Вычисление норм вектора и матрицы
> with(linalg):
> b:= vector([0,3,-4]);
> norm(b);
> M:=matrix(3,3,[-1,0,3,2,5,4,7,10,-10]);
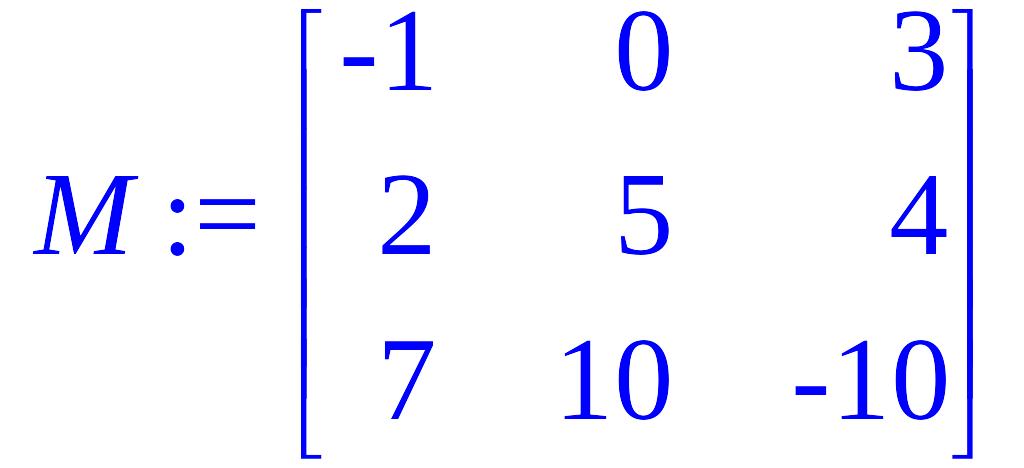
> norm(M);
>
Таблица 2.1
-
№
вар.
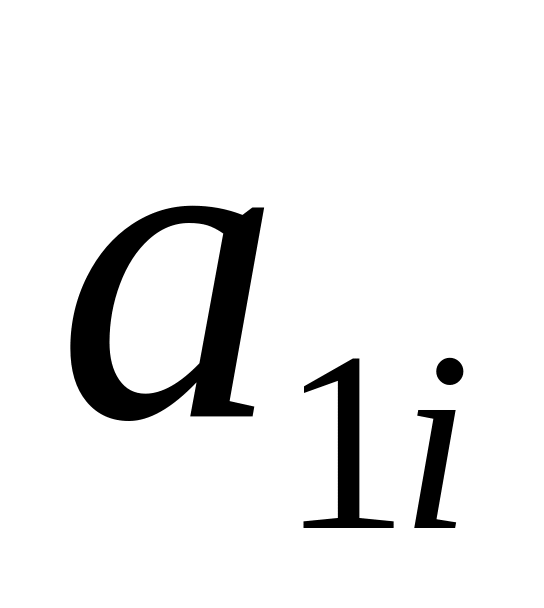
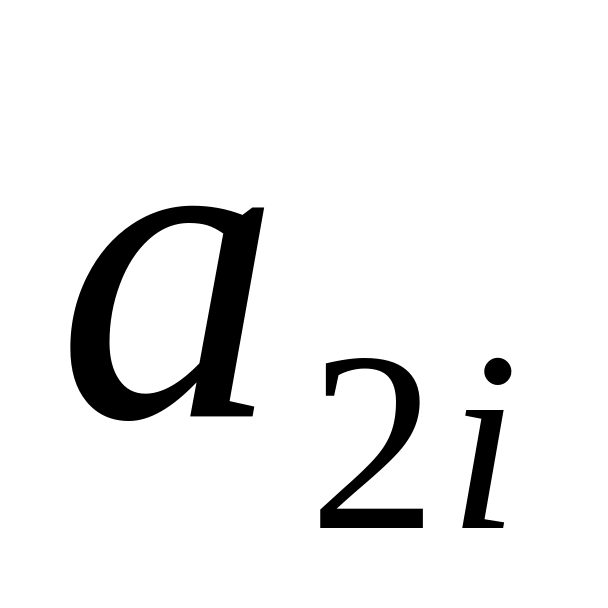
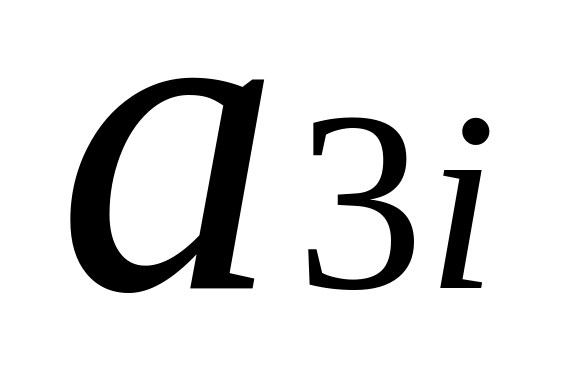
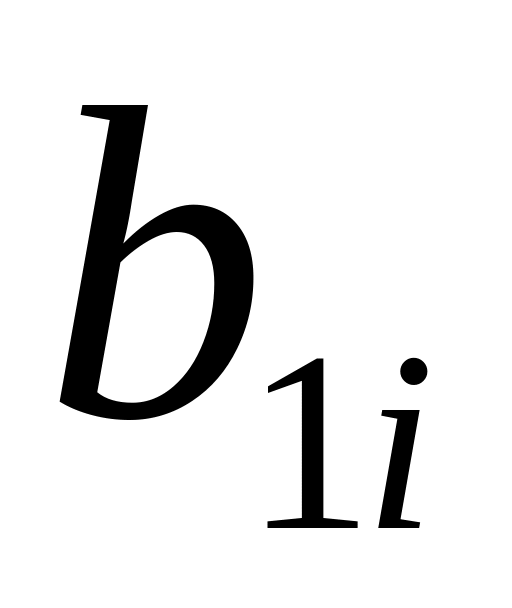
1
0.35
0.12
- 0.13
0.12
0.71
0.15
- 0.13
0.15
0.63
0.10
0.26
0.38
2
0.71
0.10
- 0.10
0.10
0.34
0.64
0.12
- 0.04
0.56
0.29
0.32
- 0.10
3
0.34
- 0.04
0.06
- 0.04
0.44
0.56
0.10
- 0.12
0.39
0.33
- 0.05
0.28
4
0.10
- 0.04
- 0.43
- 0.04
0.34
0.05
- 0.63
0.05
0.13
- 0.15
0.31
0.37
5
0.63
0.05
0.15
0.05
0.34
0.10
0.15
0.10
0.71
0.34
0.32
0.42
6
1.20
- 0.50
- 0.30
- 0.20
1.70
0.10
0.30
- 1.60
- 1.50
- 0.60
0.30
0.40
7
0.30
- 0.10
- 1.50
1.20
- 0.20
- 0.30
- 0.20
1.60
0.10
- 0.60
0.30
0.70
8
0.20
0.58
0.05
0.44
- 0.29
0.34
0.91
0.05
0.10
0.74
0.02
0.32
9
6.36
7.42
1.77
1.75
19.03
0.42
1.0
1.75
6.36
41.70
49.49
27.67
10
3.11
- 1.65
0.60
- 1.66
3.15
0.78
- 0.60
- 0.78
- 2.97
- 0.92
2.57
1.65
11
1.20
- 0.20
- 0.30
- 0.20
1.60
- 0.10
0.30
- 0.10
1.50
- 0.60
0.30
- 0.40
12
- 3
0.5
0.5
0.5
- 6
0.5
0.5
0.5
- 3
- 56.5
- 100
- 210
13
4
2
1
2
4
1
1
1
4
1
7
16
14
1
3.5
1
3
1
- 1
1
- 1
4.5
0.6
- 0.7
2.6
15
0.20
0.58
0.05
0.44
-0.29
0.34
0.05
0.81
0.20
0.74
0.02
0.32