Лабораторная работа № 5 Исследование импульсных систем

Продолжительность работы – 6 часов

Цель работы. Исследование динамических характеристик и устойчивости импульсной системы, синтез системы методом переменного коэффициента усиления.

Подготовка к работе. Изучите математическое описание импульсных преобразователей сигналов во временном и частотном пространствах, методику дискретного преобразования Лапласа и z-преобразования, аналитические и графические модели цифро-аналоговых систем, методы анализа устойчивости и качества дискретных систем, методы синтеза дискретных стабилизирующих алгоритмов.

Уясните сущность импульсной теоремы Котельникова-Шеннона и освойте способы расчёта периода дискретизации цифровых автоматических систем.

Основные теоретические положения

Получение дискретной передаточной функции

Рассмотрим дискретную систему с амплитудно-импульсной модуляцией. Ключи на входе и выходе системы замыкаются одновременно через равный промежуток (период дискретности) .

Если известна передаточная функция , то дискретную передаточную функцию (ДПФ) можно найти по теореме вычетов:

(5.1)

Дискретная передаточная функция систем с фиксатором

Реальные дискретные системы содержат фиксатор, который вносит изменения в вычисление ДПФ .

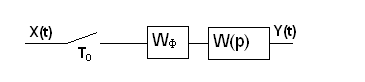
Если – передаточная функция без учета фиксатора,

– передаточная функция фиксатора (экстраполятор 0-го порядка), то дискретная передаточная функция может быть найдена следующим образом:

(5.2)

Основное условие устойчивости импульсных систем

Устойчивость импульсной системы управления, как и устойчивость непрерывной системы, определяется характером ее свободного движения. Импульсная система устойчива, если свободная составляющая переходного процесса x_с(iT₀) с течением времени затухает.

Свободная составляющая x_с(iT₀) является решением однородного разностного уравнения

(5.3)

Решение уравнения (5.3) при отсутствии у него одинаковых корней z представляет собой сумму

, (5.4)

где C_k — постоянные интегрирования, зависящие от начальных условий; z_k — корни характеристического уравнения

(5.5)

Из выражения (5.4) видно, что при i решение x_с(iT₀) стремится к нулю лишь в том случае, если все корни z_k по модулю меньше единицы, т. е. если

(5.6)

Запись (5.6) выражает общее условие устойчивости:

для устойчивости импульсной системы необходимо и достаточно, чтобы все корни характеристического уравнения системы находились внутри круга единичного радиуса с центром в начале координат.

Если хотя бы один корень z_k располагается на окружности единичного радиуса, то система находится на границе устойчивости. При |z_k|> 1 система неустойчива.

Таким образом, единичная окружность в плоскости корней z_k является границей устойчивости и, следовательно, играет такую же роль, как мнимая ось в плоскости корней р.

Можно определить устойчивость дискретной системы, не высчитывая значения корней характеристического уравнения, а пользуясь критериями устойчивости.