7)Оценка качества построенной модели. Оценка влияния значимых факторов на результат с помощью коэффициентов эластичности, β - и ∆ - коэффициентов.

Сравним индекс корреляции R и коэффициент детерминации R² полученной модели с однофакторной моделью.

Таблица 5

модель	нормир R-квадрат
парная	0,75768388
множественная	0,755539952

Из таблицы (5) видно, что качество моделей одинакова, т.к. коэффициенты одинаково близки к единице.

Теперь оценим влияние значимых факторов на результат с помощью коэффициентов эластичности, - коэффициентов с помощью формул:

, и ,

где

Х4 ср=	42,045
Х6 ср=	10,7775
Y cp=	101,2375

(см.табл.1)

1) = = 0,963- Коэффициент эластичности для фактора х4;

= - Коэффициент эластичности для фактора х6;

Отсюда видно, что при изменении Х4 на 1% значение Y увеличится на 96,3%. А при изменении Х6 на 1% значение Y увеличится на 15,2%.

2) Найдем коэффициенты β для параметра Х_4, и Х₆. Среднеквадратические отклонения определяются по формуле:

S(X4)=	20,224
S(X6)=	3,406
S(Y)=	57,291

(см.табл.1)

Тогда:

= =0,819- Стандартизованный коэф-фициент регрессии для фактора х4;

= - Стандартизованный коэф-фициент регрессии для фактора х6;

3) Вычислим коэффициенты Δ для параметров Х4 и Х6:

= 0,819 * 0,874/ 0,772 = 0,927

= 0,616 * 0,085/ 0,772 = 0,068

Из полученных данных мы видим, что доля влияния фактора площадь кухни (Х6) в суммарном влиянии всех факторов составляет 0,068 или 6,8%, тогда как доля влияния фактора жилая площадь квартиры – 0,927 или 92,7%.

Вывод:

Стоимость квартиры является эластичной переменной по отношению к фактору х4 (жилая площадь квартиры) и не эластичной по отношению к этажу и площади кухни.

Наиболее значимым фактором является фактор х4, менее значимым х6 и практически не значимым х5.

Задача №2. Исследование динамики экономического показателя на основе анализа одномерного временного ряда

В течение девяти последовательных недель фиксировался спрос Y(t) (млн.руб) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен в таблице:

Таблица 6– Исходные данные

Вариант № 10	Номер наблюдения (t=1,2,3,4,5,6,7,8,9)
	1	2	3	4	5	6	7	8	9
Y(t)	33	35	40	41	45	47	45	51	53

1. Выявление аномальных наблюдений

Построим график временного ряда

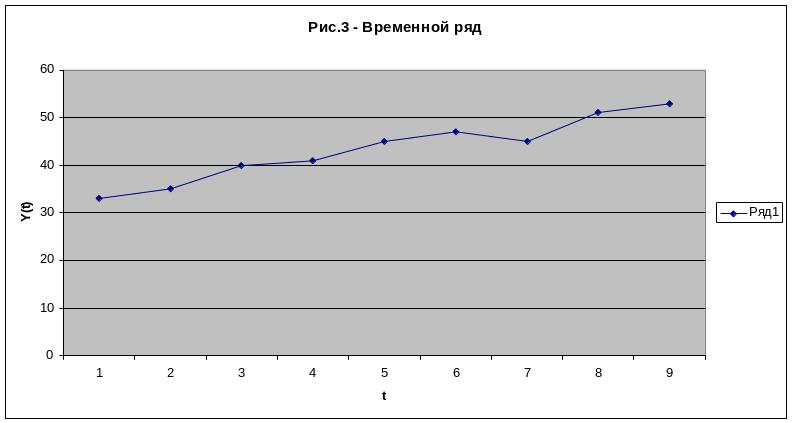
Для выявления аномальных наблюдений воспользуемся методом Ирвина. Для всех наблюдений вычисляем величину по формуле:

,

Где ,

Результаты расчетов по методу Ирвина приведены в таблице (6)

Таблица 6

t	1	2	3	4	5	6	7	8	9
yt - или у (расч.)	33	35	40	41	45	47	45	51	53
	-	0,297	0,741	0,148	0,593	0,297	0,297	0,889	0,297

По результатам расчетов аномальных наблюдений нет, т.к. расчетные величины не превышают табличных значений.

2. Постойте линейную модельŶ(t)=a0+a1*t, параметры которой оцените МНК (Ŷ(t))-расчетные, смоделированные значениявременного ряда).

Таблица 7 - Промежуточные расчеты параметров линейной модели

	Время	Показа-тель	Критерий Ирвина	Значе-ния	Значе-ния	Расчетные значения	Остаточная компонента	Поворотные точки	Значе-ние	Значение	Значение	Значе-ние
	t	y	l(расч.)	y*t	t*t	y(расч.)	e	(p)	e*e	e(t)-e(t-1)	(e(t)-e(t-1))²	A
	1	33	0,296	33	1	33,733	-0,733	¾	0,538	¾	¾	0,022
	2	35	0,741	70	4	36,133	-1,133	1	1,284	-0,400	0,160	0,032
	3	40	0,148	120	9	38,533	1,467	1	2,151	2,600	6,760	0,037
	4	41	0,593	164	16	40,933	0,067	1	0,004	-1,400	1,960	0,002
	5	45	0,296	225	25	43,333	1,667	1	2,778	1,600	2,560	0,037
	6	47	0,296	282	36	45,733	1,267	0	1,604	-0,400	0,160	0,027
	7	45	0,889	315	49	48,133	-3,133	1	9,818	-4,400	19,360	0,070
	8	51	0,296	408	64	50,533	0,467	1	0,218	3,600	12,960	0,009
	9	53	49,960	477	81	52,933	0,067	¾	0,004	-0,400	0,160	0,001
Сумма	45	390		2094	285		0,000	6	18,4	0,800	44,080	0,237
Среднее	5	43,3333		232,67	31,667	43,333	0,000	0,857	2,044	0,100	5,510	0,0263
СКО	2,739	6,745		151,43	28,08

СКО – среднеквадратичное отклонение.

Таблица 8 Линейная РЕГРЕССИЯ y=a+bt (с остатками)

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,974398
R-квадрат	0,949451
Нормированный R-квадрат	0,942229
Стандартная ошибка	1,621287
Наблюдения	9

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	345,6	345,6	131,4782609	8,6231
Остаток	7	18,4	2,628571
Итого	8	364

	Коэф-фициен-ты	Стандар-тная ошибка	t-стати-стика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересе-чение	31,3	1,178	26,602	2,717	28,548	34,118	28,548	34,118
t	2,4	0,209	11,466	8,623	1,905	2,894	1,905	2,894

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
1	33,73333	-0,73333
2	36,13333	-1,13333
3	38,53333	1,466667
4	40,93333	0,066667
5	43,33333	1,666667
6	45,73333	1,266667
7	48,13333	-3,13333
8	50,53333	0,466667
9	52,93333	0,066667
Е min =		-3,133
E max =		1,667

Рассчитываем параметры модели:

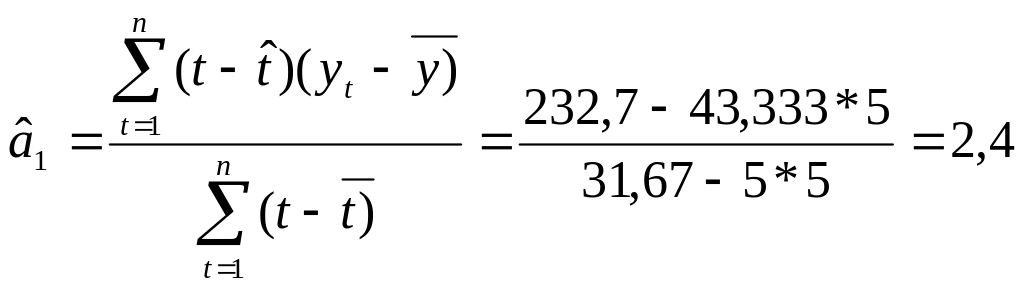
В результате расчетов получаем, что кривая роста зависимости спроса на кредитные ресурсы финансовой компании от времени имеет вид:

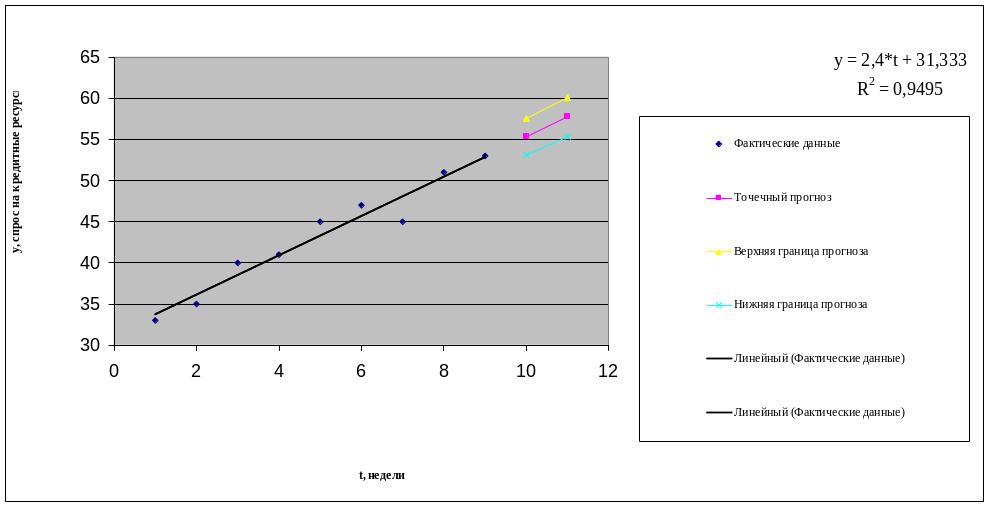
Y(t)= 31,333+2,4*t

3. Оцените адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия возьмите табулированные границы 2,7-3,7).

Проверку независимости осуществляем с помощью dw-критерия Дарбина-Уотсона по формуле:

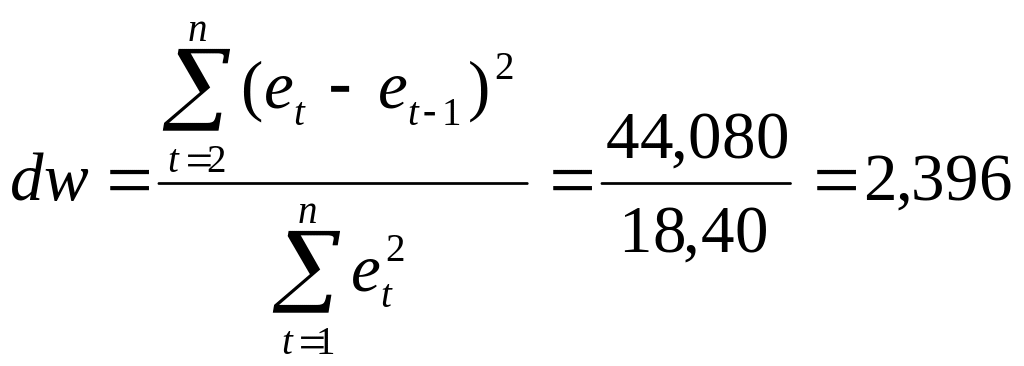
Для вычисления коэффициента Дарбина-Уотсона см.таблицу 7.

Так как dw не попало в интервал от d₂ до 2, то по данному критерию можно сделать вывод о не выполнении свойства независимости. Это означает, что в ряде динамики имеется автокорреляции, следовательно, модель по этому критерию не адекватна.

Поверку случайности проводим на основе критерия поворотных точек по формуле, количество поворотных точек р при n=9 равно 6:

р>

Рис.4 – График остатков

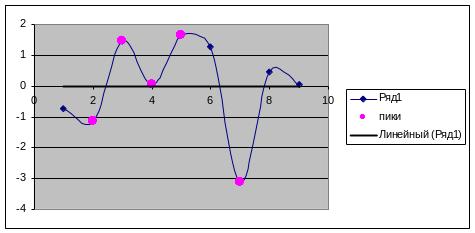
По оси х =t, по оси у – остатки

Неравенство выполняется (6>2). Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.

Вывод: значения остаточной последовательности являются случайными величинами, т.к фактическое значение поворотных точек р=6 больше чем р(критич.)=2,451.

Соответствие ряда остатков нормальному закону распределения определяем с помощью RS-критерия:

RS=(e_max-e_min)/S

Е min =	-3,133
E max =	1,667

Расчетное значение RS=2,961 в интервал (2,7 – 3,7) попадает. Следовательно, по данному критерию модель адекватна.

Вывод: модель статистически адекватна.

4) Оцените точность моделей на основе использования средней относительной ошибки аппроксимации.

Оценку точности модели проводим на основе использования средней относительной ошибки аппроксимации. Получаем

А(среднее) =0,0263*100=2,63%

Вывод: А(среднее)=5,75% - хороший уровень точности модели, т.е. точечная модель является приемлемой для прогнозирования, поскольку полученное значение <15%.

5) Осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитайте при доверительной вероятности р=70%).

Для вычисления точечного прогноза в построенную модель подставляем соответствующие значения фактора t=n+k:

Для к = 1, (t=10):

Для к = 2, (t=11):

Для построения интервального прогноза рассчитываем доверительный интервал. При уровне значимости 0,3, доверительная вероятность равна 70%, а критерий Стьюдента равен 1,895:

t cp =	5	Среднее значение наблюдений
Квадроткл (t)=	60	Квадратное отклонение наблюдений
t kp =	1,895	t-критерий Стьюдента

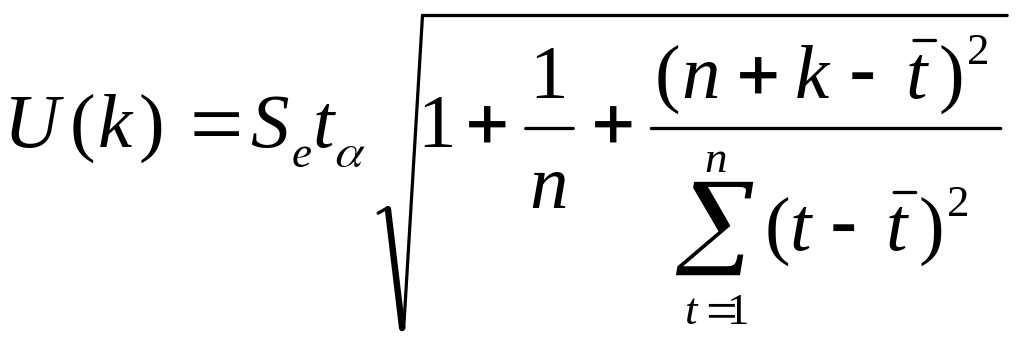
Далее вычисляем верхнюю и нижнюю границы прогноза.

Таблица 9

n+k	U(k)	Прогноз	Верхняя граница	Нижняя граница
10	U(1)=3,80	55,333	59,13	51,53667
11	U(2)=4,02	57,733	61,75135	53,71532

6) Графическое представление фактических значений показателя, результатов моделирования и прогнозирования.

Данная работа скачена с сайта Банк рефератов http://www.vzfeiinfo.ru ID работы: 28398

Данная работа скачена с сайта Банк рефератов http://www.vzfeiinfo.ru ID работы: 28398

15