ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Кафедра экономико-математических методов и моделей

КОНТРОЛЬНАЯ РАБОТА

ПО ЭКОНОМЕТРИКЕ

Вариант №10

Выполнил: ст. III курса гр.

__________________________________

Проверил: Доктор экономических наук, Половников Виктор Антонович

Москва

2011

Содержание

Задача №1. Эконометрическое моделирование стоимости квартир в московской области……………………………………………………………….3

Задача №2. Исследование динамики экономического показателя на основе анализа одномерного временного ряда………………………………………...14

Задача №1. Эконометрическое моделирование стоимости квартир в московской области

Таблица 1 - Исходные данные для эконометрического моделирования стоимости квартир

№ п/п	Y	Х4	Х5	Х6	(Х4-Х4сред)2
41	38	19	12	9,5	531,072
42	62,2	36	9	10	36,542
43	125	41	11	8	1,092
44	61,1	34,8	10	10,6	52,490
45	67	18,7	2	6	544,989
46	93	27,7	1	11,3	205,779
47	118	59	2	13	287,472
48	132	44	8	11	3,822
49	92,5	56	9	12	194,742
50	105	47	8	12	24,552
51	42	18	8	8	578,162
52	125	44	16	9	3,822
53	170	56	3	8,5	194,742
54	38	16	3	7	678,342
55	130,5	66	1	9,8	573,842
56	85	34	3	12	64,722
57	98	43	3	7	0,912
58	128	59,2	4	13	294,294
59	85	50	8	13	63,282
60	160	42	2	10	0,002
61	60	20	4	13	485,982
62	41	14	10	10	786,522
63	90	47	5	12	24,552
64	83	49,5	1	7	55,577
65	45	18,9	3	5,8	535,691
66	39	18	3	6,5	578,162
67	86,9	58,7	10	14	277,389
68	40	22	2	12	401,802
69	80	40	2	10	4,182
70	227	91	2	20,5	2396,592
71	235	90	9	18	2299,682
72	40	15	8	11	731,432
73	67	18,5	1	12	554,367
74	123	55	9	7,5	167,832
75	100	37	6	7,5	25,452
76	105	48	3	12	35,462
77	70,3	34,8	10	10,6	52,490
78	82	48	5	10	35,462
79	280	85	5	21	1845,132
80	200	60	4	10	322,382
Сумма	4049,5	1681,8	225	431,1	15950,819
Среднее	101,2375	42,045	5,625	10,7775
Среднеквадратичное отклонение	57,291	20,224	3,753	3,406

Принятые в таблице обозначения:

Y – цена квартиры – это зависимая переменная (тыс. долл.).

В качестве независимых, объясняющих переменных выбраны

Х4 –жилая площадь квартиры, кв.м;

Х5 – этаж квартиры;

Х6 – площадь кухни, кв. м.

1. Расчет матрицы парных коэффициентов корреляции; оценка статистической значимости коэффициентов корреляции.

Для вычисления матрицы парных коэффициентов корреляции используем инструмент Корреляция (Анализ данных в Excel)

Таблица 2 – Матрица парных коэффициентов корреляции

	Y	Х4	Х5	Х6
Y	1
Х4	0,874012	1
Х5	-0,07139	-0,01403	1
Х6	0,616194	0,648728	0,008149	1

Анализ матрицы парных коэффициентов корреляции показывает, что зависимая переменная (цена квартиры) имеет тесную связь с жилой площадью квартиры (r_yx3=0,874).

Оценку статистической значимости коэффициентов корреляции выполняем с использованием t-критерия Стьюдента. Фактическое значение этого критерия определяем по формуле (1):

(1)

Критическое значение t-статистики Стьюдента при уровне значимости 0,05 и числе степеней свободы 38: t_расч≈ 2,024394

Таблица 3

t - статистики для коэффициентов корреляции (t набл)
t - статистики для Х4	11,08814
t - статистики для Х5	0,441175
t - статистики для Х6	4,822883

Из таблицы (3) видно что не для всех коэффициентов матрицы t_набл > t_расч,, следовательно, только для Х4 и Х6 коэффициенты корреляции статистически значимы.

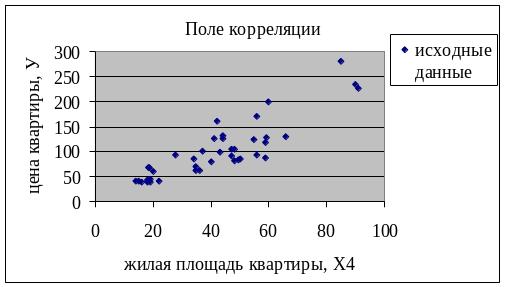
2. Построение поля корреляции результативного признака и наиболее тесно связанного с ним фактора.

Поле корреляции имеет вид, приведенный на рис.1. Вытянутость облака точек на диаграмме рассеяния вдоль наклонной прямой позволяет сделать предположение, что существует некоторая объективная тенденция прямой линейной связи между значениями переменных Х4 и Y.

3. Расчет параметров линейной парной регрессии для каждого фактора Х.

Для расчета коэффициентов регрессии используем инструмент регрессия (Анализ данных в Excel)

	Коэффициенты
Y-пересечение	-2,865
X4	2,476

	Коэффициенты
Y-пересечение	107,367
X5	-1,09

	Коэффициенты
Y-пересечение	-10,472
X6	10,365

Модели линейной регрессии будут иметь вид:

для Х4 - Y = -2,865 +2,476 X4

для Х5 - Y = 107,367 – 1,09 X5

для Х6 - Y = -10,472 + 10,365 X6

4. Оценка качества каждой модели через коэффициент детерминации, средней ошибки аппроксимации и f-критерия Фишера. Выбор лучшей модели.

Модель Х4: R² = 0,764; = 21,89%; F = 122,947.

Коэффициент детерминации равен 0,764, он показывает, что около 76,4% вариаций зависимой переменной учтено в модели и обусловлено влиянием включенных факторов, т.е. цена квартиры только на 76,4% зависит от жилой площади квартиры.

Критерий Фишера равен 122,947. Табличное значение (при k1=1, k2=38 и а=0,05) равно 4,098. Отсюда F>Fтабл. Это означает, что уравнение регрессии с вероятностью 0,95 следует признать адекватным.

Средняя ошибка аппроксимации = 21,89%, т.е расчетные значения отличаются от фактических значений на 21,89 %.

Модель Х2: R² = 0,005; = 54,09%; F = 0,195.

Коэффициент детерминации равен 0,005. Т.е. цена квартиры на 0,5% зависит от этажа квартиры.

Критерий Фишера равен 0,195. Табличное значение (при k1=1, k2=38 и а=0,05) равно 4,098. Отсюда F>Fтабл. Это означает, что уравнение регрессии с вероятностью 0,95 не следует признавать адекватным.

Средняя ошибка аппроксимации = 54,09, т.е расчетные значения отличаются от фактических значений на 54,09%.

Модель Х3: R² = 0,380; = 47,06%; F = 23,26.

Коэффициент детерминации равен 0,380. Т.е. цена квартиры на 38% зависит от площади кухни.

Критерий Фишера равен 23,26. Табличное значение (при k1=1, k2=38 и а=0,05) равно 4,098. Отсюда F>Fтабл. Это означает, что уравнение регрессии с вероятностью 0,95 следует признать адекватным.

Средняя ошибка аппроксимации = 47,06%, т.е расчетные значения отличаются от фактических значений на 47,06 %.

Исходя из полученных данных, делаем вывод, что наилучшая модель – модель Х4: Y = -2,865 +2,476 X4

Вывод:

Наилучшей из рассмотренных трех моделей линейной парной регрессии является модель регрессии между x4 и y, т.к. коэффициент детерминации имеет наибольшее значение 0,764, средняя ошибка аппроксимации - минимальное значение 21,89%, критерий Фишера - наибольшее значение 122,947.

5. Прогнозирование среднего значения показателя при уровне значимости 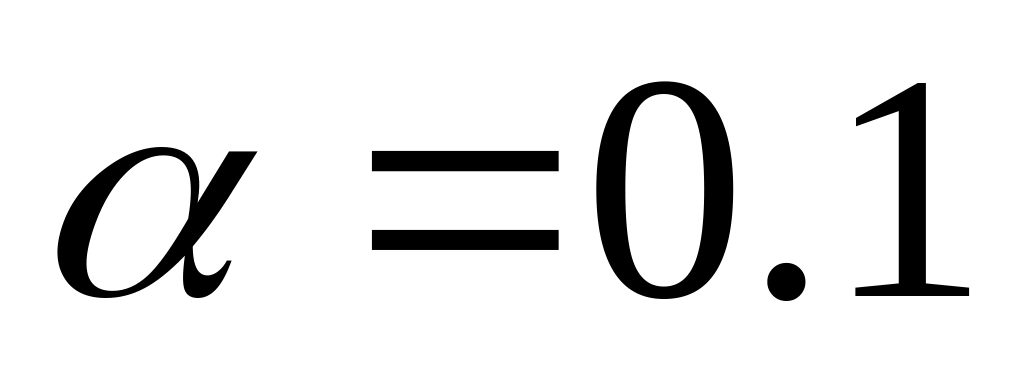, если прогнозное значения фактора 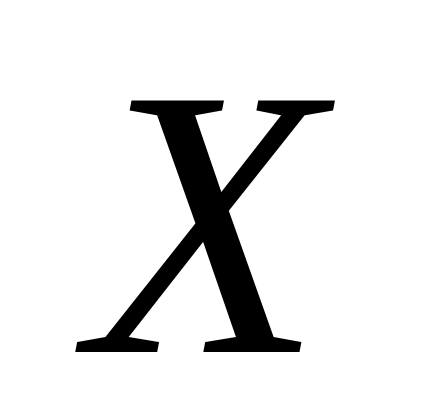составит 80% от его максимального значения.

Прогнозирование осуществим для модели Х4

Х4_max= 91

X_{прогноз} = = 72,8

из уравнение регрессии находим Y_{прогноз}:

Y_{прогноз} = -2,865+ X_{прогноз}= =177,386

Изобразим графически полученные величины (Рис.3.):