14. Что такое подстановка?

Подстановка – взаимно-однозначное (=биективное*) отображение* конечного множества Е на себя.

Подстановка конечного множества первых n натуральных чисел называется подстановкой -й степени.

Подстановка обычно записывается в виде таблицы из двух строк, где верхняя строчка – исходное множество, а нижняя – его отображение. Верхняя и нижняя строки при этом являются перестановками.

ПРИМЕР:

Запись подстановки, в которой в верхней строчке числа записаны строго по возрастанию, называется канонической.

! Перестановка столбцов в таблице никак не меняет само отображение. Например,

и

— одна и та же подстановка E₄ (двойке в верхней строке всё равно соответствует тройка в нижней и т.д). Любая перестановка приводится к каноническому виду изменением порядка столбцов – последовательным выполнением нескольких транспозиций в верхней строке и соответствующих им транспозиций в нижней строке. Т.к. одновременно меняем чётность в обеих строках, соотношение этих чётностей сохраняется.

Произведение или композиция перестановок по сути, можно понимать как действие одной перестановки на другую.

ПРИМЕР 1. Найти произведение подстановок можно так (простой прямой способ)

Первой действует подстановка слева. Первая подстановка переводит один в два, а вторая два в семь, значит произведение переводит один в семь и т.д.

ПРИМЕР 2: Также по определению произведение σ • τ можно вычислять так: в подстановке σ переставляем столбцы так, что первая строчка в σ совпадает с последней строчкой в τ. Тогда произведением будет подстановка, у которой первая строчка — стандартная, а вторая строчка — это вторая строчка из σ.

Произведение двух подстановок есть снова подстановка .

! Произведение подстановок ассоциативно: τ ∘ (σ ∘ α) = ( τ ∘ σ ) ∘ α

!! Произведение подстановок некоммутативно:  τσ ≠ στ.

Тождественная (или единичная) подстановка - отображающая каждый элемент в себя: . Например:

.

И для тождественной подстановки умножение коммутативно и равно

σ ∘ е = е ∘ σ = σ , для любой σ ∈ Sn, где Sn - группа всех возможных перестановок длины n (симметрическая группа)

! Тождественная подстановка играет роль единицы в симметрической группе Sn

Обратная подстановка σ^-1 по отношению к подстановке σ – подстановка, умножение которой слева или справа на исходную даёт тождественную подстановку.

σ ∘ σ^-1= σ^-1 ∘ σ = е

Обратная подстановка существует и является единственной для каждой σ ∈ Sn.

Таблицу обратной подстановки можно получить, если просто поменять местами верхнюю и нижнюю строки таблицы исходной подстановки. Например:

, .

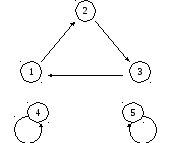
Также подстановки можно представлять:

Пример Задана подстановка .

1) в графической форме, проводя стрелки от каждого

элемента к элементу (см. рисунок)

2) строкой: f = [23145] – в строке на i-м месте стоит элемент f (i);

3) в виде произведения циклов: f = (123)(45) – каждая скобка является отдельным циклом, в каждой скобке следующий элемент получен из предыдущего, а первый элемент получен из последнего применением транспозиции.

Разложение подстановки в произведение независимых циклов устроено просто: достаточно уметь представлять цикл произвольной длины в виде произведения транспозиций. Закономерность достаточно простая: (abc)=(ab)(ac); (abcd)=(ab)(ac)(ad); (abcde)=(ab)(ac)(ad)(ae), и так далее. Каждое из равенств легко проверяется непосредственно.