
- •Дайте определение базиса векторов в пространстве.
- •Что такое направляющие косинусы вектора?
- •Сформулируйте определение треугольной матрицы
- •Сформулируйте определение трапециевидной матрицы
- •Сформулируйте определение ступенчатой матрицы
- •Сформулируйте определение единичной матрицы
- •Какие матрицы называют равными
- •Как выполняется сложение матриц?
- •Как выполняется умножение матрицы на число?
- •Свойства умножения матрицы на число (скаляр)
- •Аналогично по этому правилу можно и наоборот – вынести общий множитель с каждого элемента
- •Как выполняется умножение матриц?
- •Свойства умножения матриц:
- •Любые ли две матрицы можно перемножить?
- •Определение матрицы, транспонированной по отношению к данной.
- •Свойства транспонированной матрицы
- •Какие преобразования называют элементарными преобразованиями матриц?
- •Что такое подстановка?
- •Что такое перестановка?
- •Что такое транспозиция перестановки?
- •В каком случае два числа образуют инверсию в перестановке?
- •Сформулируйте определение минора Мij матрицы а
- •Сформулируйте определение алгебраического дополнения Аij матрицы а
- •Как изменится определитель матрицы, если 2 его строки умножить на 2?
- •Чему равен определитель матрицы, имеющий два одинаковых столбца?
- •Как изменится определитель, если у матрицы поменять местами 2 строки?
- •Чему равен определитель треугольной матрицы?
- •Чему равен определитель диагональной матрицы?
- •Сформулируйте критерии равенства нулю определителя
- •Запишите формулу для вычисления обратной матрицы
- •Свойства обратной матрицы
- •Способы вычисления определителя
- •Способы построения обратной матрицы
- •Раздел 2. Матрицы. Определители. Системы линейных уравнений Глава 2. Определители (детерминанты) квадратных матриц
- •§ 1. Перестановки и подстановки
- •§ 2. Определение детерминанта (определителя) порядка n
-
Сформулируйте определение треугольной матрицы
Треугольная матрица — это квадратная матрица, у которой все элементы, стоящие ниже (или выше) главной диагонали, равны нулю.
Подразделяется на верхнюю и нижнюю треугольные матрицы.
Верхняя
треугольная матрица - квадратная
матрица, у которой равны нулю все элементы
матрицы, расположенные под
главной диагональю, т.е. aij=0,
при всех i>j .
Например:
Нижняя треугольная матрица – это квадратная матрица, у которой равны нулю все элементы, расположенные над главной диагональю, т.е. aij=0, при всех i<j. Например:

Диагональная
матрица — квадратная матрица,
все элементы которой, стоящие вне главной
диагонали, равны нулю.
Пример:
Диагональная матрица является одновременно и верхней треугольной, и нижней треугольной. Единичная – частный случай диагональной. Как и нулевая.
! Заметьте, что в определении треугольной матрицы ничего не сказано про значения элементов, расположенных над главной диагональю или на главной диагонали. Они могут быть нулевыми или нет, – это несущественно. Это тоже треугольные матрицы:




-
Сформулируйте определение трапециевидной матрицы
Матрицу Am×n называют трапециевидной, если у нее:
- Все элементы, лежащие на главной диагонали, не равны нулю, а
- Все элементы, расположенные ниже главной диагонали, равны нулю.

В случае, если матрица не квадратная, то она будет иметь нулевые строки, если строк больше чем столбцов и не будет иметь нулевых строк, если столбцов больше чем строк.
То есть она может и не содержать нулевых строк, но уж если они есть, то располагаются внизу матрицы. Примеры трапециевидных матриц:
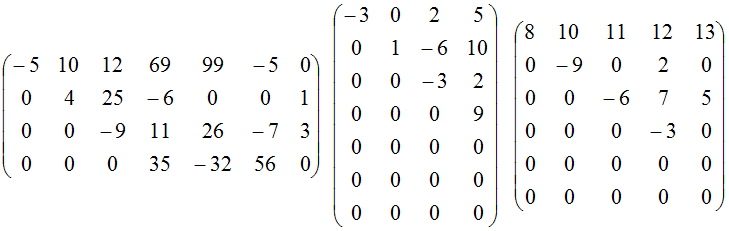
-
Сформулируйте определение ступенчатой матрицы
Матрица называется ступенчатой, если в каждой ее строке первый НЕнулевой элемент стоит правее, чем в предыдущей (т. е. получаются ступеньки и высота каждой ступеньки должна быть равна единице).
Если эта матрица содержит нулевую строку (т.е. строку, все элементы которой равны нулю), то все строки, расположенные под нею, также нулевые.
Примеры ступенчатых матриц:

То есть, если нарисовать ступеньки, увидим, что матрица ступенчатая.

Примеры НЕ ступенчатых матриц(т.к. высота ступеньки больше 1строки):

-
Сформулируйте определение единичной матрицы
Единичная матрица - квадратная матрица n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю. Обозначают E или En, где n – порядок матрицы. Например единичная матрица порядка 3 :

Единичная матрица также является треугольной, диагональной и скалярной.
-
Какие матрицы называют равными
Матрицы называются равными, если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают. То есть ВСЁ одинаковое!
! не путать с эквивалентными матрицами (см. вопрос 12)
-
Как выполняется сложение матриц?
Складывать и вычитать можно матрицы только одного размера в результате получается матрица того же размера.
Суммой двух матриц A и B порядка m×n называется матрица C=A+B того же порядка, элементы которой равны cij=aij+bij (i=1,2,...,m; j=1,2,...n).
Аналогично вычитание (разность) матриц A - B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: cij=aij - bij
Свойства сложения матриц
Из определения сложения матриц непосредственно следует, что эта операция обладает свойствами:
переместительным (коммутативным) A+B = B+A.
и сочетательным (ассоциативным) (A+B)+C = A+(B+C).
А также A + Θ = Θ + A = A, где Θ - нулевая матрица
A - A = Θ
! Складывать матрицу с числом нельзя! Матрицу можно умножить на число. Но сложить матрицу можно только с другой матрицей, причём точно такого же размера.
