ГЕОМЕТРИЯ

1. Что такое орт?

Орт – это вектор длинна которого равна единице

2. Какие векторы называют равными?

Равные вектора – это вектора которые коллинеарны и их длинны равны и направлены в одном направлении

3. Какие векторы называют коллинеарными?

Коллинеарными называют вектора лежащие на параллельных прямых или на одной прямой

4. Какие векторы называют компланарными?

Компланарными называют вектора лежащие в одной плоскости

5. Какие векторы называют линейно зависимыми?

Линейно зависимыми называют вектора если их линейная комбинация обращается в ноль при хотя бы одном ненулевом коэффициенте (один вектор выражается через другой)

6. Какие векторы называют линейно независимыми?

Линейно зависимыми называют вектора если их линейная комбинация обращается в ноль при хотя бы одном ненулевом коэффициенте (вектора не выражаются друг из друга)

7. Как связаны свойство линейной зависимости (независимости) и свойство компланарности векторов?

Вектора зависимы когда они компланарны

8. Как связаны свойство линейной зависимости (независимости) и свойство коллинеарности векторов?

Вектора зависимы когда они коллинеарны

9. Что такое линейная комбинация векторов?

Линейная комбинация векторов – это сумма векторов с некоторыми коэффициэнтами равная нуль-вектору.

10. Какой базис называют ортогональным?

Ортогональными называют базис образующие вектора которого попарно ортогональны

11. Какой базис называют ортонормированным?

Ортонормированным называют базис образующие вектора которого попарно ортогональны и равны единице

12. Дайте определение базиса векторов на плоскости.

Базисом векторов на плоскости называют два линейно независимых вектора

(Базис - упорядоченный набор векторов, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора.)

13. Дайте определение базиса векторов в пространстве.

Базисом векторов на плоскости называют три линейно независимых вектора

14. Что такое направляющие косинусы вектора?

Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора. Соответственно, координаты единичного вектора равны его направляющим косинусам.

15. Сформулируйте определение ортогональной проекции вектора на прямую.

Проекцией вектора AB на прямую называется число, равное величине отрезка A₁B₁ прямой, где точки A₁ и B₁ являются проекциями точек A и B на прямую.

16. Сформулируйте определение ортогональной проекции вектора на ось.

Проекцией вектора AB на ось L называется число, равное величине отрезка A₁B₁ оси L, где точки A₁ и B₁ являются проекциями точек A и B на ось L.

17. Продолжите формулу пра_в =

пра_b=|a|*cos(a,b)=(b*a)/|b|

18. Сформулируйте определение скалярного произведения двух векторов

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними.

Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

19. Чему равно скалярное произведение двух коллинеарных векторов?

Будет равно скалярной величине, равной произведению модулей этих векторов

20. Чему равно скалярное произведение двух ортогональных векторов

Равно 0

21. Чему равно скалярное произведение двух ортонормированных векторов?

Равно 0

22. Как вычислить скалярное произведение, если векторы заданы координатами в ортонормированном базисе?

Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

23. Сформулируйте определение векторного произведения двух векторов

Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b(|a|*|b|), перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c. |c|=|a|*|b|*sin(a,b)

24. Чему равно векторное произведение двух коллинеарных векторов?

Равно 0

25. Чему равно векторное произведение двух ортогональных векторов?

Вектору ортогональному двум умножающимся с длинной |c|=|a|*|b|

26. Чему равно векторное произведение двух ортонормированных векторов?

ВЕКТОРУ Равному 1 и направленному перпендикулярно этим двум векторам

27. Каков геометрический смысл векторного произведения?

Модуль векторного произведения равен площади параллелограмм построенного на этих векторах как на сторонах.

28. Как вычислить векторное произведение, если векторы заданы координатами в прямоугольном базисе?

С помощью матрицы, где первая строка, это ортонормированные векторы i, j, k, а вторые две строки это координаты векторов а и b.

29. Сформулируйте определение смешанного произведения двух векторов.

Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c, равное определителю матрицы построенной на этих векторах

30. Какая тройка векторов называется левой?

31. Какая тройка векторов называется правой?

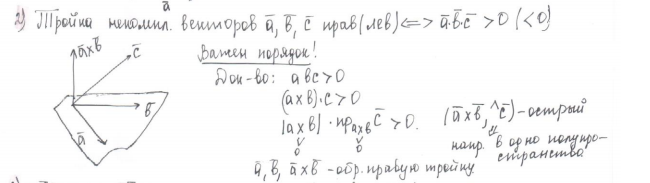
32. Как вычислить смешанное произведение, если векторы заданы координатами в прямоугольном базисе?

С помощью матрицы построенной на координатах этих векторов

33. Каков геометрический смысл смешанного произведения?

Модуль смешанного произведения трех некомпланарных векторов равен объему параллелепипеда построенного на этих векторах.

34. Сформулируйте определение алгебраической линии на плоскости

Алгебраической линией на плоскости называется множество точек плоскости, которое в какой-нибудь декартовой системе координат может быть задано уравнением вида

=0(2), где все показатели степени — целые неотрицательные числа. Наибольшая из сумм называется степенью уравнения, а также порядком алгебраической линии.

35. Сформулируйте определение трансцендентной кривой на плоскости

Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций).

36. Запишите общее уравнение прямой на плоскости.

Ах + Ву + С = 0,

37. Запишите уравнение прямой на плоскости, проходящей через заданную точку с заданным вектором нормали.

A(x-x₀)+B(y-y­₀)=0

38. Запишите каноническое уравнение прямой на плоскости.

, где р – координаты вектора нормали

39. Запишите уравнение прямой на плоскости в отрезках.

где  из общего уравнения прямой,  из общего уравнения прямой.

40. Запишите нормальное уравнение прямой на плоскости.

, где а – угол на которой нужно повернуть против часовой стрелки ось Ox до совмещения её положительного направления с направлением нормали р.

41. Запишите параметрическое уравнение прямой на плоскости.

, где р­1- х координата нормали, а р2 – у координата нормали.

42. Запишите формулу расстояния от точки до прямой на плоскости.

Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу

d =	|A·Mx + B·My + C|
	√A2 + B2

43. Запишите общее уравнение плоскости

Любую плоскость можно задать уравнением плоскости первой степени вида

Ax + By + Cz + D = 0, где A, B и C не могут быть одновременно равны нулю.

44. Запишите уравнение плоскости, проходящей через заданную точку с заданным вектором нормали.

Чтобы составить уравнение плоскости, зная координаты точки плоскости M(x0, y0, z0) и вектора нормали плоскости n = {A; B; C} можно использовать следующую формулу. A(x - x0) + B(y - y0) + C(z - z0) = 0

45. Запишите уравнение плоскости в отрезках

Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках

x	+	y	+	z	= 1
a		b		c

46. Запишите нормальное уравнение плоскости

задает в прямоугольной системе координат Oxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости 

47. Запишите формулу расстояния от точки до плоскости

Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(Mx, My, Mz) до плоскости можно найти, используя следующую формулу:

d =	|A·Mx + B·My + C·Mz + D|
	√A2 + B2 + C2

Уравнения прямой в пространстве - это уравнения двух пересекающихся плоскостей.!!

48. Запишите общее уравнение прямой в пространстве

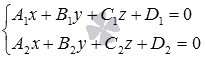 определяет координаты каждой точки прямой a, то есть, определяет прямую a. (Коэффициенты не должны быть пропорциональны)

49. Запишите каноническое уравнение прямой в пространстве

Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор  данной прямой, то  канонические уравнения этой прямой выражаются формулами:

50. Запишите параметрическое уравнение прямой в пространстве

Если известна точка , принадлежащая прямой, и направляющий вектор  данной прямой, то параметрические уравнения этой прямой задаются системой:

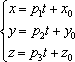
51. Запишите уравнение линии 2-го порядка

Общее уравнение линии второго порядка имеет вид , где  – произвольные действительные числа ( принято записывать с множителем-«двойкой»), причём коэффициенты  не равны одновременно нулю.

52. Запишите уравнение линии 1-го порядка

Линии, которые в декартовых координатах определяются уравнением первой степени, называются линиями первого порядка. Следовательно, каждая прямая есть линия первого порядка. Общее уравнение прямой (как общее уравнение первой степени) определяется уравнением вида: Ах + Ву + С = 0.

53. Сформулируйте определение эллипса

Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек F₁,F₂, называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: 2а. При этом расстояния между фокусами меньше данного значения: |F₁F₂|<2a.

54. Запишите каноническое уравнение эллипса

, где   – положительные действительные числа, причём число  называют большой полуосью эллипса;  число  – малой полуосью.

55. Сформулируйте определение гиперболы

Гиперболой называют множество всех точек плоскости, абсолютное значение разности расстояний до каждой из которых от двух данных точек  – есть величина постоянная, численно равная расстоянию между вершинами этой гиперболы: . При этом расстояние между фокусами превосходит длину действительной оси: .

56. Запишите каноническое уравнение гиперболы

, где   – положительные действительные числа.

57. Сформулируйте определение параболы

Параболой называется множество всех точек плоскости, равноудалённых от данной точки   и данной прямой , не проходящей через точку .

Точка  называется фокусом параболы, прямая  – директрисой

58. Запишите каноническое уравнение параболы

, где  – действительное число

59. Сформулируйте определение эксцентриситета эллипса

, которое может принимать значения в пределах , где  – это расстояние от каждого из фокусов до центра симметрии эллипса.

Эксцентриситетом гиперболы называют отношение . Так как расстояние от центра до фокуса больше расстояния от центра до вершины: , то эксцентриситет гиперболы всегда больше «единицы»: .

60. Сформулируйте определение эксцентриситета параболы

Эксцентриситет любой параболы равен единице: , r/d=1, где r - расстояние любой точки М параболы до фокуса, а d - её расстояние до директрисы.

61. Сформулируйте определение директрисы эллипса

Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения  или .

62. Сформулируйте определение директрисы гиперболы

Директрисами гиперболы называются две прямые, уравнения которых в канонической для гиперболы системе координат имеют вид . Так как , то .

( Расстояние между директрисами обозначается 2d и равно )

63. Сформулируйте оптическое свойство эллипса

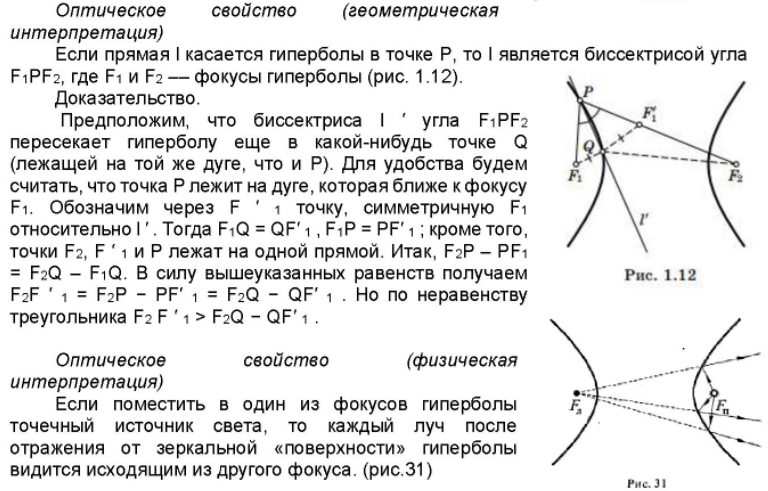
64. Сформулируйте оптическое свойство гиперболы

65. Сформулируйте оптическое свойство параболы

66. Определение алгебраической поверхности

Алгебраической поверхностью называется множество всех точек М(x,y,z) геометрического пространства, координаты которых в декартовой прямоугольной системе координат удовлетворяют алгебраическому уравнению

67. Определение трансцендентной поверхности

(как предыдущее, но нельзя описать алгебраическим уравнением)

Трансцендентной (неалгебраческой) называют поверхность, определяемую уравнением , где - трансцендентная функция (трансцендентной функцией называется аналитическая функция, не являющаяся алгебраической).

68. Запишите уравнение поверхности 2-го порядка

Общее уравнение поверхности второго порядка  Ax2+By2+Cz2+2Fyz+2Gzx+2Hxy+2Px+2Qy+2Rz+D=0, где x, y, z − координаты точек поверхности, A, B, C, … − действительные числа.

69. Запишите уравнение поверхности 1-го порядка

http://osiktakan.ru/gm06.html

70. Запишите каноническое уравнение эллипсоида

a, b, c — полуоси, a,b,c из R+

71. Запишите каноническое уравнение эллиптического параболоида

a, b из R+; a>=b

72. Запишите каноническое уравнение однополостного гиперболоида

c — действительная полуось, a и b — мнимые полуоси.

73. Запишите каноническое уравнение двуполостного гиперболоида

c — действительная полуось, a и b — мнимые полуоси

74. Запишите каноническое уравнение цилиндров 2-го порядка

Эллиптический цилиндр , a и b — полуоси

Гиперболический цилиндр

Параболический цилиндр , p — фокальный параметр

75. Запишите каноническое уравнение конусов 2-го порядка

Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат

АЛГЕБРА

1. Определение и основные термины у матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

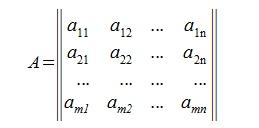
или  (i=1,2,...m; j=1,2,...n).

Числа a_ij входящие в состав данной матрицы называются ее элементами, а первый индекс i означает номер строки, а второй индекс j - номер столбца.

Матрица-строка ( или ВЕКТОР-строка) матрица размером 1×n, т.е. состоящая из одной строки. Например:

Матрица столбец (или ВЕКТОР-столбец) - матрица размером m×1, т.е. состоящая из одного столбца. Например

Квадратная матрица - матрица, у которой количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например матрица третьего порядка:

Элементы расположенные на местах a₁₁, a₂₂ ,..., a_nn  (то есть элементы с m=n) образуют  главную диагональ матрицы. Например:

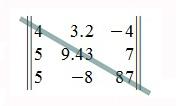
Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами.

Можно записать так:

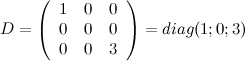
В случае НЕ квадратной матрицы m×n - матриц элементы a_ii ( i=1,2,...,min(m,n)) тоже всё равно образуют главную диагональ. Например:

Элементы расположенные на местах a_31n, a_2n-1 ,..., a_n1 образуют побочную диагональ матрицы. Например:

Нулевая матрица – матрица, у которой все её элементы равны нулю. Например, нулевая матрица 2 × 3

След матрицы: сумма главных диагональных элементов матрицы A  называется следом матрицы и обозначается Sp A или Tr A. Например:

Главным элементом некоторой строки матрицы  называется ее первый (по порядку) ненулевой элемент.

Главные элементы каждой строки данной матрицы будут: главный элемент первой строки и главный элемент второй строки

Скалярной называется диагональная матрица , у которой все диагональные элементы равны между собой. Частные случаи – единичная и нулевая квадратные матрицы.