2.1.3. Вязкость жидкости

Вязкость жидкостей (внутреннее трение) обусловлена сцеплением между ее молекулами.

Уравнение Ньютона:

,

где – коэффициент вязкости, – градиент скорости течения жидкости, – площадь соприкосновения слоев жидкости.

Ламинарное и турбулентное течения. Слоистое течение жидкости называют ламинарным. Наличие скорости течения вязкой жидкости вследствие неоднородности давления по поперечному сечению трубы создает завихрения, и движение становится вихревым или турбулентным.

Характер течения жидкости по трубе зависит от свойств жидкости, скорости её течения, размеров трубы и определяется числом Рейнольдса:

,

где – плотность жидкости, – диаметр трубы.

Если число Рейнольдса больше некоторого критического, то движение жидкости будет турбулентным. Например, для гладких цилиндрических труб критическое значение числа Рейнольдса составляет 2300.

На шарик, движущийся в вязкой жидкости, действуют три силы:

сила тяжести

,

выталкивающая сила (сила Архимеда)

,

сила вязкого трения, которая выражается формулой Стокса

,

где – радиус шарика, – плотность материала шарика, – плотность жидкости, – коэффициент внутреннего трения (вязкость) жидкости, – скорость движения шарика.

При увеличении скорости падающего тела сила возрастает, и если путь падения шарика внутри жидкости достаточно велик, то при условии движение шарика будет равномерным со скоростью . Для установившегося равномерного движения справедливо равенство

.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

№ 2.10

Во сколько раз увеличится скорость оседания эритроцитов у людей, больных сфероцитозом, по сравнению с нормой, если средний радиус эритроцита при этом заболевании возрастает в 1,5 раза?

Решение

Равномерное оседание эритроцитов происходит при следующем условии:

, (1)

где – сила тяжести, действующая на эритроцит массой , плотностью и радиусом , – сила сопротивления, действующая на эритроцит со стороны воды плотностью и вязкостью , – сила Архимеда, действующая на эритроцит. Тогда соотношение (1) перепишется:

. (2)

Отсюда

.

Из последнего соотношения выразим скорость оседания эритроцитов:

. (3)

Запишем (3) для эритроцитов радиусом в норме и для эритроцитов радиусом при сфероцитозе:

. (4)

. (5)

Деля (5) на (4) и подставляя значения радиусов и , получим:

.

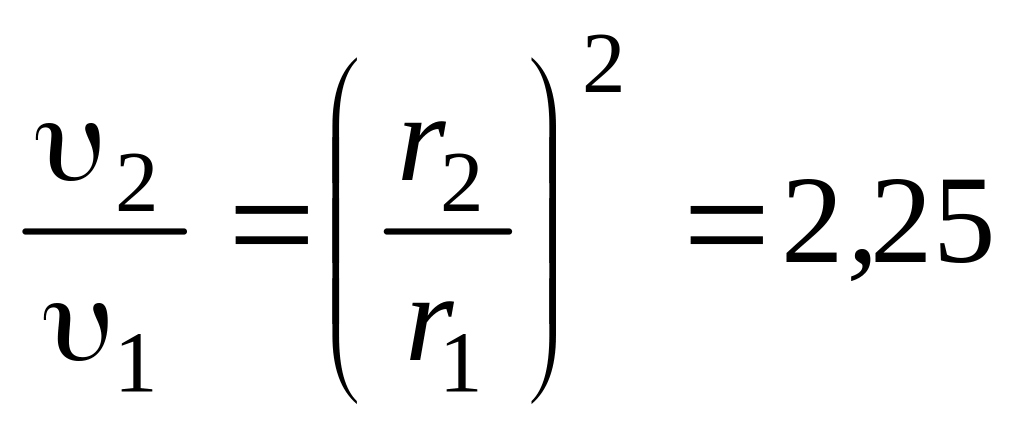№ 2.11

Определите максимальное количество крови, которое может пройти через аорту в 1 с, чтобы течение сохранялось ламинарным. Диаметр аорты см, вязкость крови мПа∙с, плотность крови кг/м³.

Решение

Число Рейнольдса , устанавливает границу между ламинарным и турбулентным течениями жидкости. По определению

, (1)

где – скорость течения крови через аорту, – кинематическая вязкость крови. Из (1) выразим скорость:

. (2)

Тогда, учитывая выражение (2), а также то, что объем крови, протекающей через сосуд, , где – сечение аорты, масса крови, протекающей через аорту, будет равна:

. (3)

Подставляя численные значения величин, входящих в (3), получим:

кг.

№ 2.12

При прямых измерениях артериального давления в артерию вводится игла, соединенная гибким шлангом со стеклянной трубкой, установленной вертикально. На какую максимальную высоту поднимется кровь в трубке, если систолическое артериальное давление мм рт. ст.? Плотность крови кг/м³, плотность ртути кг/м³.

Решение

Высоту подъема крови в стеклянной трубке можно определить из условия:

. (1)

Отсюда

. (2)

Для проведения расчетов следует перевести значение систолического давления в Паскали по формуле:

, (3)

где мм – соответствующая этому давлению высота столба ртути.

Подставляя (3) в (2), получим:

. (4)

Подставляя численные значения величин, входящих в (4), получим:

м.

№ 2.13

При некоторых заболеваниях критическое число Рейнольдса в сосудах принимает значение . Найдите скорость движения крови, при которой возможен переход ламинарного течения в турбулентное в сосуде диаметром мм. Плотность крови кг/м³, вязкость крови мПа∙с.

Решение

Число Рейнольдса устанавливает границу между ламинарным и турбулентным течениями жидкости. По определению

, (1)

где – скорость течения крови, – диаметр кровеносного сосуда, – кинематическая вязкость крови, – ее плотность. Из (1) выразим скорость кровотока:

. (2)

Подставляя численные значения величин, входящих в (2), получим:

м/с.

№ 2.14

Вследствие потери упругих свойств сосудов при атеросклерозе число Рейнольдса существенно изменяется. Определите число Рейнольдса в сосуде диаметром мм, в котором скорость движения крови м/с. Принять плотность крови кг/м³, а вязкость крови Па·с.

Решение

Число Рейнольдса может быть рассчитано по известной формуле:

.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Определите гидравлическое сопротивление аорты диаметром 1,75 см на участке длиной 3 см.

2. При ламинарном течении через сечение артерии равное 0,5 см² за 2 с проходит 10 мл крови. Какова при этом вязкость крови?

3. Определите скорость оседания эритроцитов диаметром 6 мкм в растворе плотностью 10³ кг/м³ и вязкостью 4 мПа, полагая, что плотность крови составляет 1060 кг/м³.

4. Рассчитайте число Рейнольдса для крови при линейной скорости кровотока 0,5 м/с, вязкости крови 5 мПа и диаметре сосуда 0,6 см. Плотность крови принять равной 1060 кг/м³.

5. Во сколько раз изменилась вязкость крови при патологии по сравнению с нормой, если линейная скорость кровотока уменьшилась в 1,5 раза, а плотность крови возросла на 10%? Число Рейнольдса постоянно.