2.1.2. Поверхностное натяжение

Коэффициент поверхностного натяжения (поверхностное натяжение) равен изохорно-изотермической работе , необходимой для увеличения площади поверхности жидкости на единицу:

.

Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия поверхности жидкости пропорциональна ее площади.

Коэффициент поверхностного натяжения может быть определен как модуль силы поверхностного натяжения , действующей на единицу длины линии , ограничивающей поверхность:

.

Вблизи границы раздела между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела. Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом , называемым краевым углом.

Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол оказывается тупым. В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании , при полном несмачивании .

Над искривленной поверхностью жидкости возникает избыточное давление , называемое лапласовским:

,

где – радиус кривизны мениска жидкости.

Под действием лапласовского давления происходит подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются.

Подъем жидкости в капилляре продолжается до тех пор, пока лапласовское давление не станет равным гидростатическому давлению столба жидкости:

,

где – плотность жидкости, – высота капиллярного подъема.

Отсюда следует:

.

При полном смачивании , . В этом случае

.

При полном несмачивании , и, следовательно, . Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр. Вода практически полностью смачивает чистую поверхность стекла.

Условием отрыва капли от капиллярной трубки является равенство ее веса в момент отрыва силе поверхностного натяжения, действующей вдоль ее шейки:

где – радиус перетяжки капли, – масса капли.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

№ 2.5

Какой диаметр имеет перетяжка при отрыве капли дистиллированной воды массой мг? Поверхностное натяжение воды мН/м, плотность – кг/м³.

Решение

Отрыв капли произойдет в момент равенства ее веса силе поверхностного натяжения, действующей вдоль ее шейки:

(1)

где – радиус перетяжки капли, – ускорение свободного падения.

Из (1) можно выразить радиус перетяжки капли:

. (2)

Подставляя численные значения величин, входящих в (2), получим:

м.

Диаметр перетяжки будет мм.

№ 2.6

В ряде случаев лекарство дозируют каплями. На сколько процентов изменится доза водного раствора лекарства при изменении температуры от ⁰C до ⁰C? Этим температурам соответствуют значения поверхностного натяжения мН/м и мН/м.

Решение

На основе рассуждений, приведенных в предыдущей задаче, можно записать:

(1)

откуда можно выразить массу капли:

. (2)

Запишем выражение (2) для температур и , которым соответствуют значения масс капель и :

. (3)

. (4)

Из (3) и (4) определим изменение дозы раствора:

. (5)

Подставляя численные значения величин, входящих в (5), получим:

.

№ 2.7

В горизонтально расположенный капилляр набирают мл крови, так что длина столбика составляет см. Сколько крови останется в капилляре, если его поставить вертикально? Учесть, что верхний конец капилляра остается открытым. Поверхностное натяжение крови Н/м, плотность кг/м³.

Решение

Высота подъема жидкости по вертикальному капилляру определяется выражением:

, (1)

где – радиус капилляра.

Для нахождения радиуса капилляра воспользуемся соотношением:

, (2)

где – сечение трубки. Из последнего соотношения выразим радиус трубки:

. (3)

Подставляя выражение для радиуса из (3) в (1), получим:

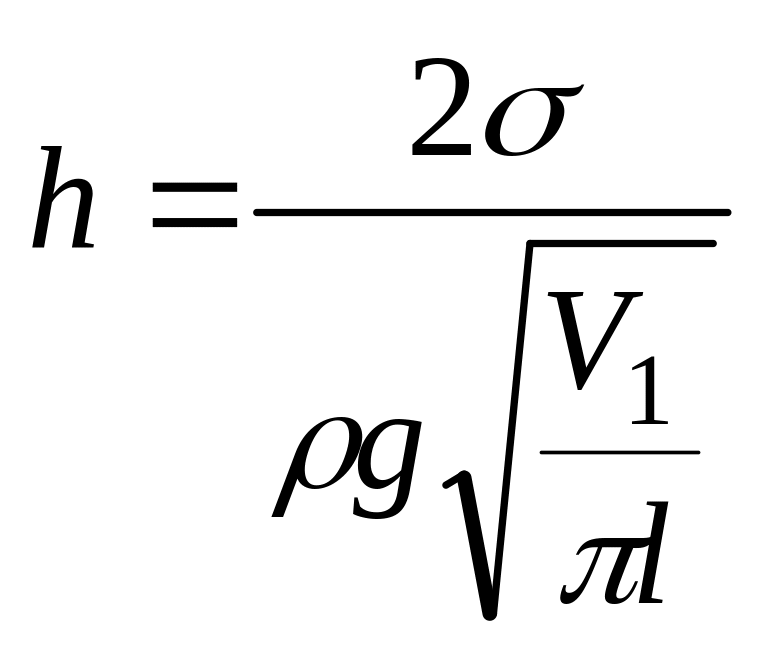. (4)

Подставляя численные значения величин, входящих в (4), получи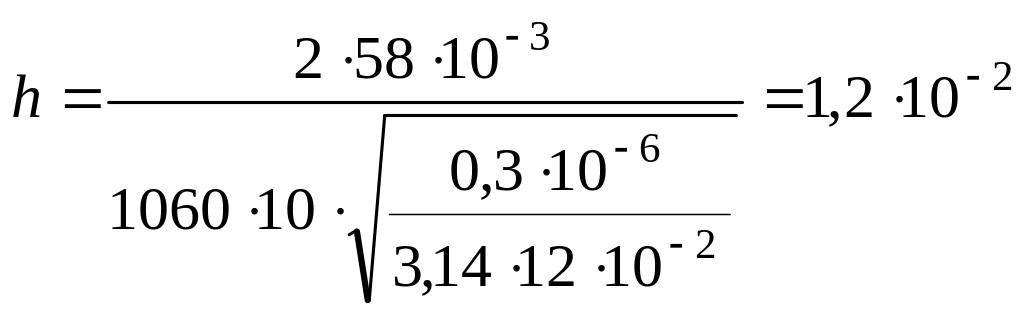м:

м.

№ 2.8

Предметное стекло микроскопа имеет вид круга диаметром мм. На него нанесли капельку крови массой г и наложили другое такое же стеклышко. В результате оба стеклышка слиплись. С какой силой , перпендикулярной поверхности стеклышек, надо растягивать их, чтобы разъединить? Считать, что проба крови полностью смачивает стекло, и поэтому меньший радиус кривизны боковой поверхности кровяного слоя равен половине расстояния между стеклышками. Поверхностное натяжение крови Н/м, плотность кг/м³.

Решение

При растягивании стеклышек к ним прилагается сила

, (1)

где – избыточное давление над искривленной поверхностью жидкости радиусом , – площадь поверхности стеклышек. Поскольку в разъединении стеклышек участвует 2 поверхности, выражение (1) следует переписать в виде:

. (2)

Масса крови, находящейся между стеклышками, равна:

, (3)

где – объем слоя крови между пластинками. Из (3) можно выразить :

. (4)

По условию задачи

. (5)

Из выражения для избыточного давления, а также соотношения (5) можно найти искомую силу :

. (6)

Подставляя численные значения величин, входящих в (6), получим:

мН.

№ 2.9

Кровь в капилляре поднялась на высоту мм. Определите коэффициент поверхностного натяжения крови, если внутренний диаметр трубки мм.

Решение

Подъем крови в трубке будет продолжаться до тех пор, пока избыточное давление над искривленной поверхностью жидкости не уравняется гидростатическим давлением . В этих соотношениях – коэффициент поверхностного натяжения крови, – ее плотность, – радиус капиллярной трубки.

Таким образом, можно записать:

. (1)

Из последнего соотношения можно выразить :

. (2)

Подставляя численные значения величин, входящих в (2), получим:

мН/м.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Каково поверхностное натяжение физраствора, если масса 50 капель, вытекших из капельницы диаметром 2 мм, составила 2 г?

2. Определите, во сколько раз изменится поверхностное натяжение физраствора при его нагревании, если при одной и той же дозировке до нагревания раствора образовалось 50 капель, а после нагревания – 60?

3. На какую высоту поднимется кровь плотностью 1060 кг/м³ в капиллярной трубке диаметром 0,5 мм? Поверхностное натяжение крови принять равным 58 мН/м.

4. Определите диаметр иглы капельницы, если при инфузии жидкого препарата плотностью 950 кг/м³ масса отрывающейся капли составляет 4 мг. Поверхностное натяжение раствора принять равным 40 мН/м.

5. Какова плотность жидкого раствора, поднимающегося в капиллярной трубке диаметром 1 мм на высоту 2 см? Поверхностное натяжение раствора принять равным 65 мН/м.