1.3. Колебания и волны

Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса.

Период колебаний – это время, за которое совершается одно полное колебание.

Частота колебаний – это число колебаний, совершаемых за единицу времени.

Фаза колебания – это величина, характеризующая положение колеблющегося тела в данный момент времени.

Амплитуда колебания – это максимальное значение колеблющейся величины.

Уравнение гармонических колебаний имеет вид: , где – амплитуда колебаний, – круговая частота колебаний, – линейная частота колебаний, – период колебаний, – начальная фаза колебаний, – фаза колебаний. В уравнении гармонических колебаний наряду с синусом используется и косинус.

Частота колебаний математического маятника определяется выражением:

,

где – длина маятника

Частота колебаний пружинного маятника определяется выражением:

,

где – жесткость пружины, – масса груза.

Механическая волна – это механическое возмущение, распростра- няющееся в пространстве и несущее энергию.

Уравнение волны:

,

где – смещение точки, участвующей в волновом процессе, – амплитуда волны, – ее круговая частота, – фаза волны, – время, – произвольная координата, – скорость распространения волны.

Связь между длиной волны и скоростью ее распространения выражается формулой:

,

где – частота волны.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

№ 1.12

Материальная точка массой г колеблется согласно уравнению . Найдите максимальную силу, действующую на точку, и ее полную энергию. Величина смещения задается в сантиметрах.

Решение

В соответствии со вторым законом Ньютона сила, действующая на материальную точку, определяется выражением

, (1)

где – ускорение точки, которое может быть найдено как вторая производная смещения по времени . Найдем первую производную:

. (2)

Найдем вторую производную:

. (3)

Максимальное значение косинуса – 1. Поэтому абсолютное значение ускорения см/с². Тогда максимальная сила, действующая на точку, будет равна: Н.

Максимальная энергия точки определится как

, (4)

где – максимальная скорость колебаний, которая равна первой производной , максимальное значение которой равно 20. Т.е. см/с. Тогда

Дж.

№ 1.13

Для проверки слуха применяется камертон. Какова частота его колебаний, если наименьшее расстояние между точками волны, колеблющимися в одинаковых фазах, м? Скорость распространения звука в воздухе принять м/с.

Решение

Наименьшее расстояние между точками, колеблющимися в одинаковых фазах, равно длине волны, которая определяется выражением

,

где – период колебаний камертона, – частота. Отсюда определим частоту колебаний:

с^-1.

№ 1.14

Определите разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии см друг от друга. Скорость пульсовой волны м/с, колебания сердца считать гармоническими с частотой Гц.

Решение

Длине волны соответствует разность фаз , а расстоянию – разность фаз , которую следует определить. Составим пропорцию:

. (1)

Учитывая, что , из пропорции (1) найдем:

. (2)

Подставляя численные значения величин, входящих в (2), получим:

.

№ 1.15

Разность хода звуковых волн, приходящих в левое и правое ухо человека, составляет см. Определите сдвиг фаз между обоими звуковыми ощущениями для тона частотой Гц.

Решение

Длине волны соответствует разность фаз , а расстоянию – разность фаз , которую следует определить. Составим пропорцию:

. (1)

Учитывая, что , из указанной пропорции найдем:

. (2)

Подставляя численные значения величин, входящих в (2), получим:

.

№ 1.16

Определите разность фаз двух точек волны, отстоящих друг от друга на расстоянии см. Скорость волны м/с, частота – Гц.

Решение

По аналогии с предыдущей задачей

№ 1.17

Число сердечных сокращений у пациента при брадикардии составило ударов в минуту. Какова длина математического маятника, имеющего такую же собственную частоту колебаний?

Решение

Частота колебаний математического маятника определяется выражением:

, (1)

где – ускорение свободного падения, – длина маятника. Возводя обе части (1) в квадрат и подставляя численные значения входящих в (1) величин, найдем длину маятника:

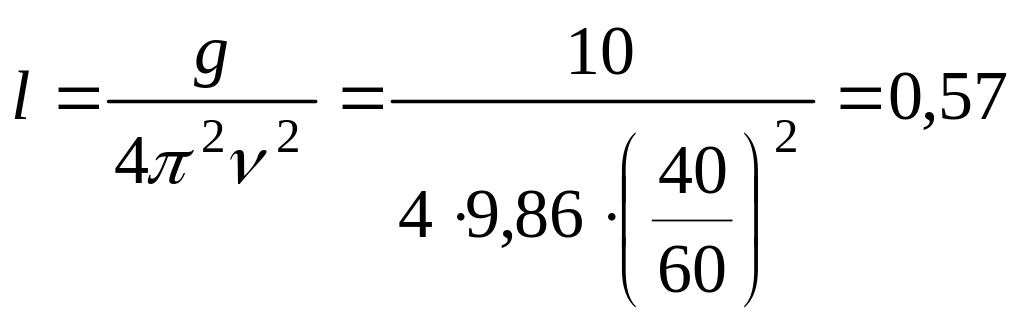м.

№ 1.18

Число сердечных сокращений у пациента при тахикардии составляет ударов в минуту. Груз какой массы следует подвесить к пружине жесткостью Н/м, чтобы он совершал колебания с такой же частотой?

Решение

Частота колебаний пружинного маятника определяется выражением

, (1)

где – масса груза. Возводя обе части (1) в квадрат и выражая массу груза, получим:

. (2)

Подставляя численные значения величин, входящих в (2), получим:

кг.

№ 1.19

Пики электрокардиограммы на миллиметровой ленте имеют амплитуду мм при частоте сердечных сокращений ударов в минуту. Записать уравнение колебаний, которому подчиняется сердце, считая их гармоническими.

Решение

Воспользуемся уравнением гармонических колебаний в виде:

. (1)

Подставляя численные значения величин, входящих в (1), получим:

.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Какова периодичность сердечных сокращений, если сердце за одну минуту совершает 80 ударов?

2. Разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии 0,1 м друг от друга, составляет 90⁰. Какова при этом скорость пульсовой волны, если частота сердечных сокращений составляет 2 Гц?

3. Запишите уравнение колебаний, описывающее сердечные сокращения при частоте 2 Гц. Амплитуду сигнала электрокардиографа считать равной 1 см.

4. Сигнал, регистрируемый электрокардиографом, изменяется по закону 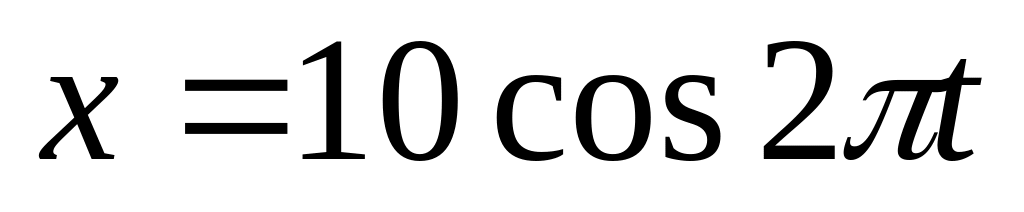. Какова при этом частота сердечных сокращений у пациента?

5. Какова длина математического маятника, колеблющегося с частотой равной частоте сердечных сокращений при 80 ударах в минуту?