2.3. Кровообращение

Кровь представляет собой вязкую жидкость, которая прогоняется сердцем через сложную систему артерий и вен. Скорость течения крови достаточно мала, так что поток можно считать ламинарным без турбулентностей. Кровеносные сосуды можно считать цилиндрическими.

Объем жидкости, протекающий за 1с через горизонтальную трубку, выражается формулой Пуазейля:

,

где – радиус трубки, – вязкость жидкости, – длина трубки, – разность давлений на её концах. Здесь видно, что при увеличении радиуса трубки в два раза, возрастает в 16 раз. Если что-либо приведет к утолщению артериальных стенок, что уменьшит , ослабевший поток крови может вызвать грудную жабу. Наиболее распространенная причина грудной жабы – артериосклероз, повреждение артерий.

Гидравлическое сопротивление. Величина называется гидравлическим сопротивлением. Оно тем больше, чем больше вязкость , длина трубы , и меньше площадь поперечного сечения трубы.

Пульсовая волна – это распространяющаяся по аорте и артериям волна повышенного давления, вызванная выбросом крови из левого желудочка в период систолы.

Скорость пульсовой волны в крупных сосудах определяется выражением:

,

где – модуль упругости стенки сосуда, – плотность вещества сосуда, – толщина стенки сосуда, – диаметр сосуда.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

№ 2.29

Определите среднюю линейную скорость кровотока в сосуде радиусом см, если во время систолы через него протекает мл крови. Считать длительность систолы с.

Решение

Объем крови, протекающей через кровеносный сосуд, определяется выражением:

, (1)

где - линейная скорость кровотока, - сечение сосуда. Выражая из (1) скорость кровотока и подставляя численные значения величин, заданных в условии задачи, получим:

м/с.

№ 2.30

Наблюдая под микроскопом движение эритроцитов в капилляре, можно измерить скорость течения крови ( мм/с). Средняя скорость тока крови в аорте составляет cм/c. На основании этих данных определите, во сколько раз сумма поперечных сечений всех функционирующих капилляров больше сечения аорты.

Решение

Запишем уравнение неразрывности струи:

, (1)

где – сечение капилляра, – сечение аорты. Выразим из (1) отношение

: . (2)

Подставляя численные значения величин, входящих в (2), получим:

.

№ 2.31

Найдите объемную скорость кровотока в аорте, если радиус просвета аорты см, а линейная скорость крови в ней м/с.

Решение

Объемная скорость кровотока может быть выражена через линейную скорость течения крови соотношением:

,

где – сечение аорты. Учитывая это и подставляя численные значения, можно получить:

м³/с.

№ 2.32

Средняя линейная скорость кровотока в сонной артерии радиусом см равна 5 мм/с. Какова объемная скорость кровотока в этом сосуде?

Решение

Объемная скорость кровотока может быть выражена через линейную скорость течения крови соотношением:

,

где – сечение артерии. Учитывая это и подставляя численные значения, можно получить:

м³/с.

№ 2.33

Скорость течения крови в капиллярах составляет м/с. Чему равна скорость крови в аорте , если суммарная площадь сечения капилляров в 800 раз больше площади сечения аорты ?

Решение

Запишем уравнение неразрывности струи для кровотока:

.

Отсюда выразим и рассчитаем скорость кровотока в аорте:

м/с.

№ 2.34

Каково гидравлическое сопротивление кровеносного сосуда длиной м и радиусом мм? Вязкость крови принять равной мкПа·с.

Решение

Из формулы Пуазейля запишем выражение для гидравлического сопротивления:

.

Подставляя численные значения величин, входящих в приведенное выражение, получим:

Па·с/м³.

№ 2.35

При чуме артерия сужается в 2 раза. Во сколько раз при этом изменится объемная скорость кровотока?

Решение

Согласно формуле Пуазейля объемная скорость кровотока определяется выражением

. (1)

где – радиус артерии, – разность давлений на ее концах, – коэффициент вязкости крови, – длина артерии. Запишем (1) для двух значений радиусов артерии и :

. (2)

. (3)

Деля (2) на (3) и подставляя численные значения величин, заданных в условии задачи, находим искомую величину:

.

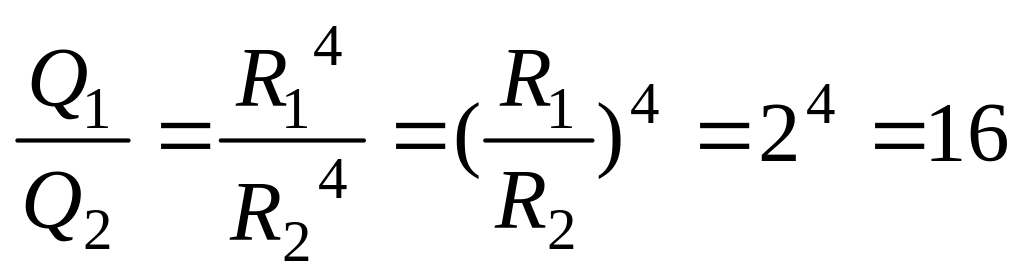№ 2.36

При некоторых заболеваниях критическое число Рейнольдса в сосудах становится равным . Найдите скорость движения крови, при которой возможен переход ламинарного течения в турбулентное в сосуде диаметром мм.

Решение

Число Рейнольдса устанавливает границу между ламинарным и турбулентным течениями жидкости. По определению

, (1)

где – скорость течения крови, – диаметр кровеносного сосуда, – кинематическая вязкость крови, – ее плотность. Из (1) найдем скорость кровотока:

м/с.

№ 2.37

Вследствие потери упругих свойств сосудов при атеросклерозе число Рейнольдса существенно изменяется. Определите число Рейнольдса в сосуде диаметром мм, в котором скорость движения крови м/с. Принять плотность крови кг/м³, а вязкость крови Па·с.

Решение

Число Рейнольдса может быть рассчитано по известной формуле:

.

№ 2.38

Во сколько раз изменяется модуль упругости стенки аорты при атеросклерозе, если известно, что скорость пульсовой волны возросла в три раза?

Решение

Скорость пульсовой волны определяется по формуле Моенса – Кортевега:

, (1)

где – модуль упругости стенки сосуда, – толщина стенки сосуда, – ее плотность, – внутренний радиус сосуда. В норме (1) запишется:

. (2)

При атеросклерозе (1) запишется:

. (3)

Деля (3) на (2) и проводя сокращения, получим:

. (4)

Возводя обе части (4) в квадрат и подставляя численные значения, получим:

.

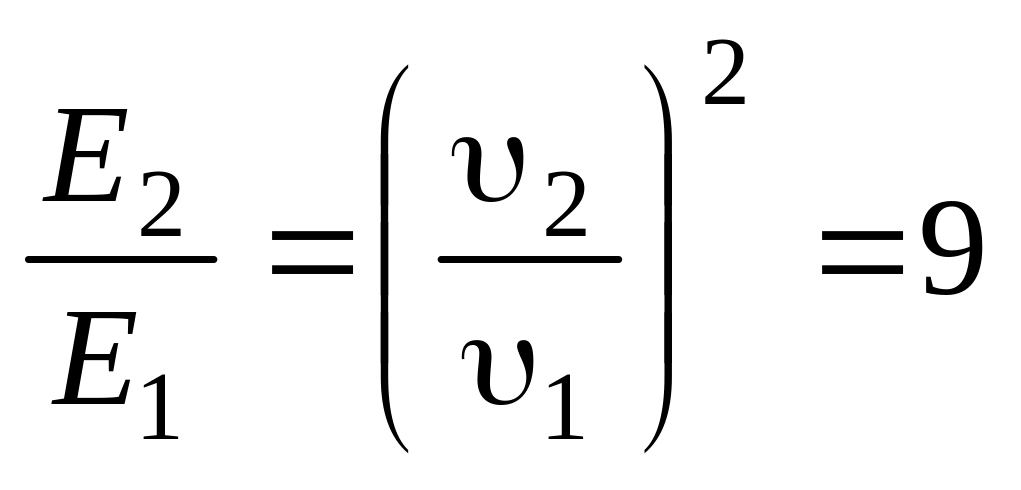№ 2.39

Скорость пульсовой волны в артериях составляет м/с. Чему равен модуль упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки сосуда равно 6, а плотность стенок сосуда г/см³?

Решение

Скорость пульсовой волны в кровеносных сосудах определяется по формуле Моенса-Кортевега:

.

Выражая из указанного соотношения модуль упругости и подставляя численные значения, получим:

Па

№ 2.40

Определите работу, совершаемую сердцем при сокращении левого желудочка, если в аорту со скоростью м/с выбрасывается мл крови при давлении в сосуде кПа.

Решение

Динамическое давление, при котором происходит выброс ударного объема крови в артерию, равно давлению в сосуде:

. (1)

При этом сердцем совершается работа:

. (2)

Подставляя численные значения величин, входящих в выражение (2), получим:

Дж.

№ 2.41

Найдите мощность, развиваемую сердцем человека при его сокращении продолжительностью с. Ударный объем крови мл, скорость крови в аорте м/с. Среднее давление, при котором кровь выбрасывается в аорту левым желудочком, кПа. Учесть, что работа правого желудочка составляет 20 % работы левого. Плотность крови кг/м³.

Решение

Работа сердца складывается из работы , совершаемой левым желудочком, и работы , совершаемой правым желудочком:

. (1)

Работа, совершаемая левым желудочком, определяется выражением

. (2)

Поскольку работа, совершаемая правым желудочком , полная работа сердца

. (3)

Подставляя значение из (2) в (3), получим:

. (4)

Подставляя численные значения величин, входящих в (4), получим:

Дж.

Теперь легко рассчитать мощность сердца:

Вт.

№ 2.42

Найдите кинетическую энергию объема крови , протекающего за время мин со скоростью м/с через артерию диаметром мм.

Решение

Кинетическая энергия крови массой определяется выражением:

. (1)

Учитывая, что , где – плотность крови, (1) можно переписать:

. (2)

Объем крови определяется выражением , где – сечение сосуда. С учетом этого (2) можно переписать:

. (3)

Подставляя численные значения величин, входящих в (3), получим:

Дж.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Гидравлическое сопротивление кровеносного сосуда длиной 2 см составляет 10¹³ Па·с/м³. Определите радиус сосуда.

2. Определите скорость пульсовой волны в артериях, полагая, что модуль упругости этих сосудов равен 9·10⁵ Па, отношение радиуса просвета к толщине стенки сосуда равно 6, а плотность стенок сосуда 1 г/см³.

3. Объемная скорость кровотока при склерозе сосудов уменьшилась в 2 раза. На сколько процентов уменьшился при этом внутренний диаметр сосуда?

4. Рассчитайте объемную скорость кровотока в сосуде длиной 6 см и диаметром 2 мм, если разность давлений на его концах составляет 16 Па. Вязкость крови принять равной 5000 мкПа∙с.

5. Под каким давлением выбрасывается в аорту кровь из левого желудочка, если при этом сердце совершает работу в 1 Дж? Ударный объем крови принять равным 50 мл, скорость кровотока в аорте – 0,5 м/с.

ТАБЛИЦА СООТВЕТСТВИЯ НОМЕРОВ ЗАДАЧ, ПРИВЕДЕННЫХ В ПОСОБИИ, С НОМЕРАМИ ЗАДАЧ, ПРИВЕДЕННЫХ В СБОРНИКЕ ЗАДАЧ А.Н. РЕМИЗОВА И А.Г. МАКСИНОЙ

Номера задач по пособию	Номера задач по задачнику А.Н. Ремизова	Номера задач по пособию	Номера задач по задачнику А.Н. Ремизова
№1.4	2-174	№2.11	2.145
№1.5	2-177	№2.13	2.181
№1.9	2-35	№2.14	2.186
№1.10	2-36	№2.20	2.130
№1.11	2.144	№2.22	2-134
№1.12	2-42	№2.25	2.132
№1.14	2-83	№2.26	2.135
№1.15	2-84	№2.28	2.137
№1.16	2-111	№2.29	2-152
№1.20	2-86	№2.30	2.131
№1.21	2-92	№2.31	2.170
№1.22	2-93	№2.32	2.180
№1.23	2-99	№2.33	2.188
№1.24	2-102	№2.34	2-167
№1.25	2-104	№2.35	2.158
№1.28	2.171	№2.36	2.181
№1.29	2.172	№2.37	2.186
№2.5	2-146	№2.39	2-169
№2.6	2-147	№2.40	2.156
№2.7	2-150	№2.41	2.160
№2.10	2-161	№2.42	2.157