МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«КАБАРДИНО-БАЛКАРСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ им. Х.М. БЕРБЕКОВА»

МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА

ЗАДАЧИ ПО МЕДИЦИНСКОЙ

И БИОЛОГИЧЕСКОЙ ФИЗИКЕ

Специальности:

060101.65 Лечебное дело

060105.65 Стоматология

060109.65 Сестринское дело

Нальчик – 2012 г.

УДК 61:53(07)

ББК 5:22.3я73

К - 88

Рецензент:

доктор физико-математических наук, профессор,

заведующий отделом ГУ ВГИ

Б.А. Ашабоков

Составители: Кумыков В.К., Абазова З.Х., Петросян Э.О., Борукаева И.Х.

Механика. Молекулярная физика. Задачи по медицинской и биологической физике. Методические рекомендации по решению задач. – Нальчик: Каб.-Балк. ун-т, 2012.

Настоящие методические рекомендации по решению задач соответствуют разделам «Механика» и «Молекулярная физика» курса медицинской и биологической физики. Всего в издание включено подробное описание решений 70 наиболее типичных задач различной степени сложности. В начале каждого раздела приводятся теоретические сведения и формулы по тематике раздела, а в конце – задачи для самостоятельного решения.

Методические рекомендации предназначены для студентов, обучающихся по медицинским специальностям 060101.65 Лечебное дело, 060105.65 Стоматология и 060109.65 Сестринское дело.

Рекомендовано РИС университета

УДК 61:53(07)

ББК 5:22.3я73

 Кабардино-Балкарский государственный университет им. Х.М. Бербекова, 2012

СОДЕРЖАНИЕ

Предисловие …………………………………………………………………………4

1. Механика ……………………………………………………………………...5

1.1. Деформации ……………………………………………………………..5

1.2. Вращательное движение ………………………………………………10

1.3. Колебания и волны …………………………………………………….16

1.4. Звук ……………………………………………………………………..22

1.5. Эффект Доплера ……………………………………………………….27

2. Молекулярная физика ………………………………………………………33

   1. Свойства жидкостей ………………………………………………….33

2.1.1. Влажность воздуха ……………………………………………...33

2.1.2. Поверхностное натяжение ……………………………………...38

2.1.3. Вязкость ………………………………………………………….45

2.2. Движение идеальной жидкости……………………………………..50

2.3. Кровообращение ……………………………………………………..61

Таблица соответствия номеров задач, приведенных в пособии, с номерами

задач, приведенных в сборнике задач А.Н. Ремизова и А.Г. Максиной ……….71

Литература …………………………………………………………………….........72

Предисловие

Предлагаемые вашему вниманию методические рекомендации предназначены для проведения занятий по решению задач (в рамках часов, отводимых на самостоятельную работу) со студентами медицинских специальностей 060101.65 Лечебное дело, 060105.65 Стоматология и 060109.65 Сестринское дело. Они охватывают материал, соответствующий разделам «Механика» и «Молекулярная физика», изучаемым в рамках курса медицинской и биологической физики. Настоящие рекомендации являются одной из первых попыток частичного восполнения существующего пробела в отечественной учебно-методической литературе, посвященной описанию методов решения задач по медицинской и биологической физике.

В пособии приводятся подробные решения 70 наиболее типичных задач различной сложности. При отборе задач преимущество отдавалось тем, которые имеют непосредственное отношение к будущей специальности. Примерно 60 % задач, приведенных в «решебнике» отобраны из «Сборника задач по медицинской и биологической физике» А.Н. Ремизова и А.Г. Максиной, рекомендованного в 2001 году Министерством образования РФ в качестве основного учебного пособия (задачника) для студентов медицинских специальностей. Остальные задачи составлены авторами.

Каждый параграф предваряет необходимый студентам для решения задач теоретический материал с формулами, который соответствует основному учебнику по физике для медицинских специальностей «Медицинская и биологическая физика» А.Н. Ремизова и др., выпущенного в 2008 году издательством «Дрофа». Все параграфы завершаются задачами для самостоятельного решения студентами.

1. Механика

1.1. Деформации

Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.

Существует несколько видов деформаций твердых тел. Простейшим видом деформации является деформация растяжения или сжатия. Ее можно характеризовать абсолютным удлинением , возникающим под действием внешней силы . Связь между и зависит не только от механических свойств вещества, но и от геометрических размеров тела (его толщины и длины).

Отношение абсолютного удлинения к первоначальной длине образца называется относительным удлинением или относительной деформацией :

.

Отношение модуля внешней силы к площади сечения тела называется механическим напряжением :

.

За единицу механического напряжения в СИ принят паскаль (Па).

При малых деформациях связь между и оказывается линейной. При этом при снятии напряжения деформация исчезает. Такая деформация называется упругой. В пределах упругой деформации сила упругости прямо пропорциональна абсолютной деформации (закон Гука):

.

Знак минус означает, что сила упругости противоположна направлению смещения при деформации; – жесткость, – начальная длина стержня, – модуль упругости (модуль Юнга). Модуль Юнга численно равен напряжению, при действии которого длина тела при деформации удваивается.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

№ 1.1

Модуль Юнга поясничного позвонка составляет примерно Н/м². Найдите силу , действующую на позвонок, если его абсолютная деформация равна мм, длина костной пластинки см, толщина см, ширина см.

Решение

По определению напряжение деформации костной пластинки равно силе, действующей на единицу площади сечения костной пластинки , т.е.

, (1)

где

. (2)

С другой стороны, напряжение деформации определяется выражением:

. (3)

Объединяя (1), (2) и (3), можно выразить искомую силу:

. (4)

Подставляя численные значения величин, входящих в (4), получим:

Н.

№ 1.2

При операции в кость помещена стальная скоба (стержень) сечением мм². Считая стенки кости неподвижными и абсолютно жесткими, рассчитайте силу давления скобы на стенки кости при нагревании на 5 К. Между скобой и костью зазор отсутствует. Коэффициент линейного расширения стали К^-1, модуль упругости Н/м².

Решение

Костная ткань обладает упругими свойствами, поэтому сила давления скобы будет равна силе упругости ткани. Силу упругости можно найти из закона Гука:

, (1)

где – коэффициент жесткости кости, – ее деформация, – начальная длина.

С учетом этого (1) можно переписать:

. (2)

Для нахождения используем формулу для линейного расширения при нагревании:

. (3)

Подставляя (3) в (2), получим:

. (4)

Подставляя численные значения величин, входящих в (4), найдем модули искомой силы:

Н.

№ 1.3

Упругость мышцы пропорциональна ее поперечному сечению и составляет в среднем Н/м². Определите мощность, развиваемую мышцей при сокращении на м, если ее поперечное сечение м², а продолжительность сокращения с.

Решение

Мощность, развиваемая мышцей при ее сокращении, определяется как

, (1)

где – работа, совершаемая мышцей при ее сокращении, – усилие, развиваемое мышцей при ее сокращении.

Поскольку упругость мышцы , то . Подставляя выражение для в (1), получим выражение для мощности:

. (2)

Подставляя численные значения величин, входящих в (2), получим:

Вт.

№ 1.4

Определите абсолютное удлинение сухожилия длиной мм и площадью поперечного сечения м² под действием силы Н. Модуль упругости сухожилия Па. Считать сухожилие абсолютно упругим телом.

Решение

Согласно закону Гука

, (1)

где – механическое напряжение, возникающее в сухожилии под действием силы , – относительное удлинение сухожилия длиной . С учетом этого (1) можно переписать:

. (2)

Выражая из (2) , получим:

. (3)

Подставляя численные значения величин, входящих в (3), получим:

м.

№ 1.5

Нагрузка на бедренную кость, составляющая Н, при сжатии вызывает относительную деформацию . Найдите эффективную площадь поперечного сечения кости, если ее модуль упругости Па.

Решение

В соответствии с законом Гука

, (1)

где – механическое напряжение, возникающее в бедренной кости под действием силы , – относительное удлинение бедренной кости длиной . С учетом этого (1) можно переписать:

. (2)

Выражая из (2) , получим:

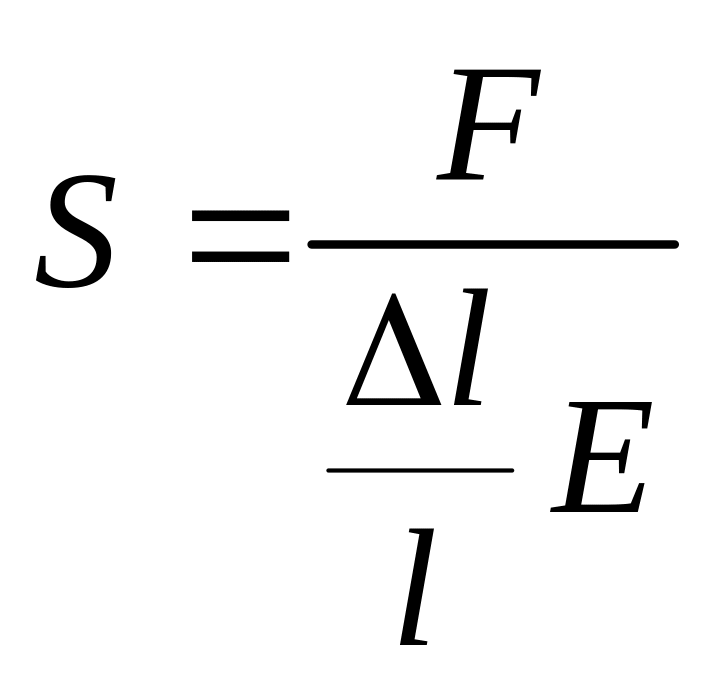. (3)

Подставляя численные значения величин, входящих в (3), получим:

м².

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Для растяжки кости при переломе к металлической проволоке подвешивается груз массой 3 кг. На сколько при этом удлинится проволока, если ее жесткость составляет 100 кН/м?

2. Какое напряжение возникает в металлической проволоке цилиндрической формы, используемой в травматологии для растяжки костей при переломах, при подвешивании к ней груза массой 5 кг? Диаметр проволоки – 1 мм, жесткость – 140 кН/м.

3. Определите модуль Юнга позвонковой кости, если при воздействии на нее силы 4000 Н ее абсолютная деформация составляет 1,2 мм. Длина костной пластинки – 2,7 см, толщина – 4 см, ширина – 2,5 см.

4. Во сколько раз изменится модуль упругости берцовой кости человека при увеличении нагрузочного напряжения на нее от 10 Па до 20 Па, если при этом относительная деформация кости возросла с 0,03 до 0,08?

5. Определите сечение костной ткани, если механическое напряжение, возникающее в ней при ее растяжении силой 100 Н, составляет 10⁴ Н/м².