Распределение Гаусса.

Распределение Гаусса является предельным случаем распределения Пуассона и многих других законов распределения.

Рассмотрим распределение Пуассона при больших n и n₀. Дискретность распределения в этом случае теряет свое значение, т.к. n меняется практически непрерывно.

Будем характеризовать отклонение n от n₀ помощью , определенного соотношением

Ограничимся рассмотрением случая, когда   1.

Подставляя формулу Стирлинга

в (4), найдём

,

откуда

Вспоминая теперь, что , а (n – n₀) просто равно отклонению n от среднего значения n₀, по­лучим закон распределения Гаусса, описывающий поведение непрерывных величин,

(8)

С помощью формулы (8) нетрудно найти вероятность того, что значение х измеренной ве­личины лежит между X₁ и Х₂:

(9).

Интеграл (9) не сводится к элементарным функциям. Он выражается обычно через функ­цию Ф(х):

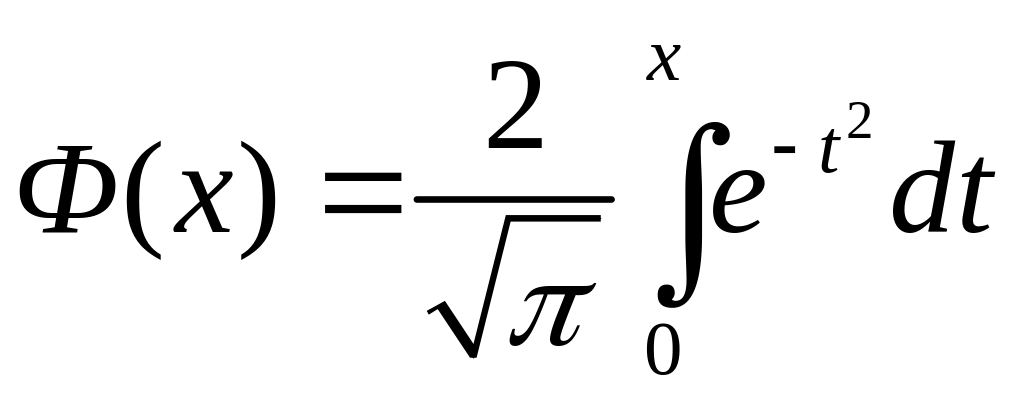(10)

Как нетрудно убедиться,

(11)

Определенная формулой (10) функция Ф является функцией толь­ко х. Эта функция изо­бражена на рис. 2 для х>0. Значения Ф(х) при х<0 находятся с помощью соотношения

Ф(–х) = – Ф(х) (12).

Оценки для вероятности откло­нения на  и 2 легко получить с помощью формул (11) и (12) и графика функции Ф(х) на рис.2.

Метод наименьших квадратов.

Рассмотрим опыт по определе­нию модуля растяжения метал­лического стержня. Результаты измерений удлинения стержня под нагрузкой могут быть представлены в виде таблицы.

Нагрузка	Xl	X2	…	Хn
Удлинение	Y1|	Y2	…	Yn

Согласно закону Гука зависимость удлинения от нагрузки имеет вид

y=kx (13).

Неизбежные ошибки опыта приводят, однако, к тому, что точки (х_i, у_i) не лежат на одной прямой. Значение к может быть найдено из любой пары значений (х_i, у_i) а наличие n пар приводит к появлению n, вообще говоря, несовместных уравнений для нахождения k.

Задачу о выборе наилучшего значения можно решать графически, отмечая точки на миллиметровой бумаге и проводя через них на глаз наилучшую прямую. Графический способ решения не всегда, однако, обеспечивает достаточную точность. Аналитическое решение задачи производится с помощью метода наименьших квадратов. Сущность метода такова. Рассмотрим отклонение точек (х_i, у_i) от прямой (13) и составим величину  – сумму квадратов вертикальных отклонений наших точек от прямой:

(14).

Величина  всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое его значение, при котором  имеет минимум.

Дифференцируя , найдем:

или

(15)

Вычисление показывает, что стандартная ошибка (k) определения величины k равна при этом

(16)

Мы рассмотрели сейчас наиболее простой случай применения метода наименьших квадратов. Рассмотрим теперь несколько более трудный случай, когда точки должны удов­летворять не формуле (13), а несколько более сложной формуле

у=а+bх (17)

Задача состоит в том, чтобы по имеющемуся набору значений (х_i ,y_i) найти наилучшие значения а и b.

Снова составим квадратичную форму, равную сумме квадратов отклонений точек от закона(17),

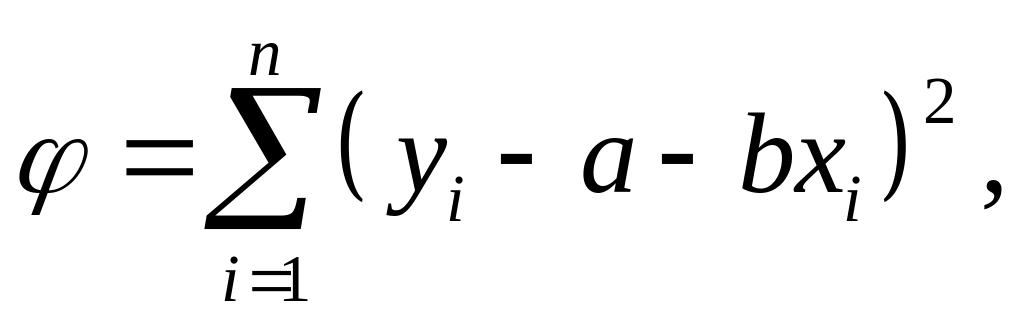
и найдем значения а и b, при которых имеет минимум :

Совместное решение этих уравнений дает

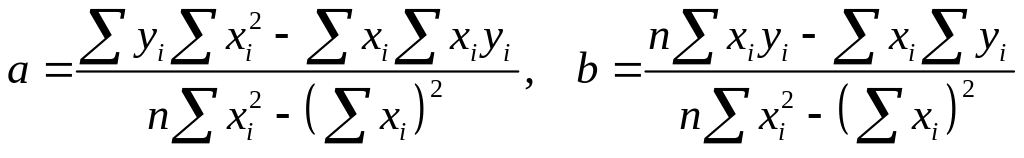(18).

Формулы (18) принимают более простой вид, если ввести :

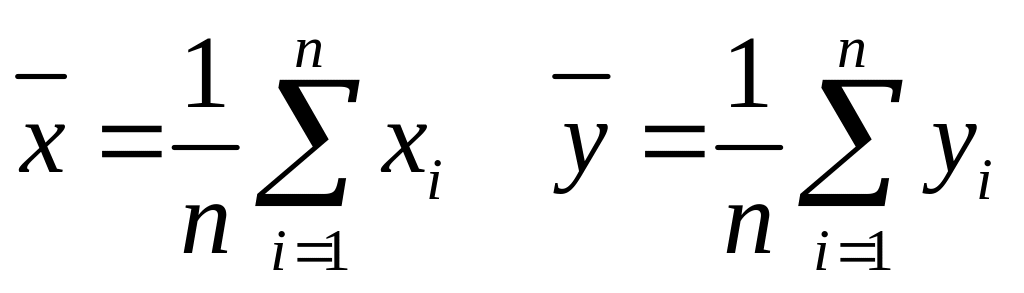(19).

Подстановка (19) в (18) дает

(20)

Стандартные ошибки определения a и b равны:

(21).

Формулы (15) и (20) дают аналитический способ проведения прямой через заданные экспериментальные точки.