Лабораторная работа №4 «Изучение движения тела по окружности под действием силы тяжести и упругости»

Цель работы: доказать, что при движении тела по окружности под действием силы тяжести и силы упругости равнодействующая этих сил равна произведению массы тела на центростремительное ускорение, которое тело получает в результате действия на него этих сил.

Гипотеза: предположим, что закон Ньютона при движении тела по окружности и изменение движения тела под действием силы не соответствуют.

Оборудование:

• штатив с муфтой и кольцом;

• груз из набора по механике массой 50г, закрепленный на нити;

• лист бумаги с начерченной окружностью радиусом 15 см;

• динамометр;

• секундомер;

• измерительная лента.

Теория:

П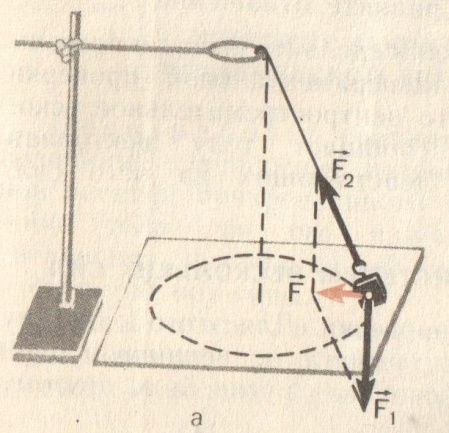 ри движении тела по окружности (конический маятник) на тело действуют две силы: сила тяжести 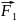и сила натяжения нити .

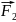Их равнодействующая .

Она и сообщает телу центростремительное ускорение .

где R – радиус окружности, по которой движется тело; N – число оборотов маятника; t – время “N” оборотов,

т.е. модуль результирующей силы можно рассчитать по формуле 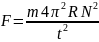(1) и можно измерить при помощи динамометра, скомпенсировав ее силой упругости динамометра:

С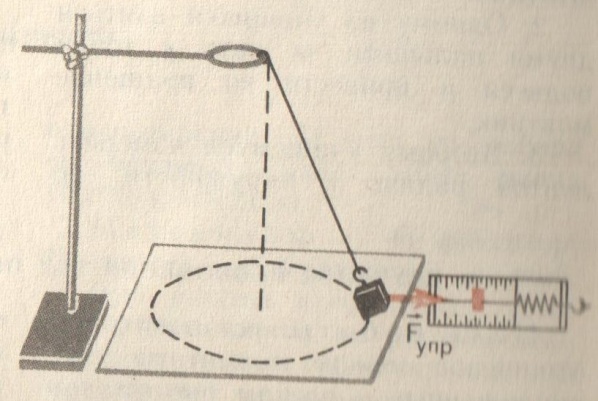 равнив результирующую, определенную разными способами, можно сделать вывод о движении тела по окружности под действием силы тяжести и силы упругости

Ход работы:

1. Закрепить груз на нити длиной 45-50 см и прикрепить к кольцу штатива.

2. Привести груз во вращение по окружности, очерченной на бумаге.

3. Измерить время 20 или 30 полных оборотов маятника.

4. Измерения повторить 3 раза.

5. Рассчитать .

6. По формуле (1) рассчитать результирующую силу F.

7. Измерить результирующую силу при помощи динамометра.

8. Занести данные в таблицу.

9. Сравнить отношение с единицей, оценить погрешность.

№ оп.	t, c	∆t, c	tср, с	N, об	m, кг	∆m, кг	R, м	∆R, м	F, H	Fупр, Н	∆Fупр, Н
1	26,1	0,005	26,2	20	0,05	0,5*10-3	0,15	0,05*10-2	0,17	0,15	0,005
2	26,0			20	0,05		0,15
3	26,5			20	0,05		0,15

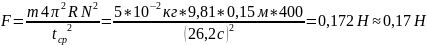
F_упр=0,15 Н

Рассчитаем погрешность: 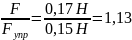или относительная погрешность .

Вывод: результаты работы показали, что при движении тела по окружности, результирующая сил тяжести и упругости, в пределах погрешности, равна произведению массы на центростремительное ускорение .

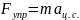Лабораторная работа №5 «Определение коэффициента трения скольжения разными способами»

Цель работы: Опытным путем определить коэффициент трения при скольжении деревянного бруска по металлической поверхности.

Оборудование:

• деревянный брусок;

• металлический трек;

• измерительная лента с миллиметровыми делениями;

• набор грузов;

• динамометр;

• штатив с креплениями для регулирования высоты наклонной плоскости.

Теория:

1 способ (динамический):

П ри равномерном скольжении бруска по горизонтальной плоскости силу трения можно рассчитать по формуле: ,

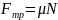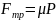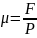т.к. , , откуда (1)

2 способ (статический):

У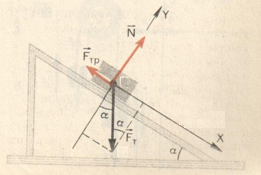 становить металлическую плоскость наклонно, добиваясь равномерного скатывания бруска с нее. По II закону Ньютона: . В значениях проекций на координатные оси:

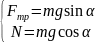
Решая систему уравнений, получаем

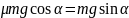
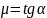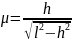, следовательно, (2).

Ход работы:

1 способ:

1. Определить вес деревянного бруска с помощью динамометра.

2. Равномерно перемещая брусок по горизонтальной металлической поверхности, измерить силу тяги, которая будет равна силе упругости динамометра.

3. Рассчитать коэффициент трения по формуле (1).

4. Вычислить погрешность измерения µ.

5. Данные внести в таблицу:

F, H	∆F, H	P, H	∆P, H	µ1	Ɛµ	∆ µ1
0,22	0,01	0,96	0,01	0,23	0,055	0,013

.

.

.

(*)

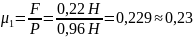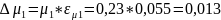2 способ:

1. Закрепить наклонную плоскость на такой высоте, чтобы брусок соскальзывал с нее равномерно.

2. Измерить высоту и длину наклонной плоскости.

3. По формуле (2) рассчитать коэффициент трения µ.

4. Вычислить погрешность измерения.

5. Данные внести в таблицу:

h, м	∆ h, м	l, м	∆ l, м	µ2	Ɛµ	∆ µ2
0,16	5*10-4	0,6	5*10-4	0,235	0,7%	0,0017

Рассчитаем µ₂ по формуле (2):

.

Относительная погрешность:

.

.

(**)

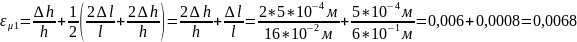Вывод: Определили двумя способами коэффициент трения скольжения дерева по металлу, получили и . Значения равны (совпадают) в пределах погрешности, следовательно, можно утвердить, что коэффициент трения данного деревянного бруска по металлической поверхности µ≈0,23.