Определители порядка

Пусть - квадратная матрица порядка , т.е. таблица из чисел . Числа называются элементами матрицы , индексы указывают номер строки и столбца элемента .

Рассмотрим произведение элементов, лежащих по одному в каждой строчке и каждом столбце и запишем его в виде . Индексы образуют перестановку чисел . С помощью инверсий (перестановок пары чисел) эта перестановка может быть приведена к . Произведение снабдим знаком «+», если четное, и знаком «–», если нечетное.

Определитель матрицы равен алгебраической сумме всех произведений вида , снабженных указанным выше знаком.

Определитель матрицы задается формулой

, где сумма берется по всем перестановкам чисел .

Для определителя порядка выполняются те же свойства (1 – 6), что и для определителей третьего порядка. Для вычисления определителя - го порядка применяются описанные ранее методы разложения по строке (столбцу) и линейные преобразования строк (столбцов).

Задача 5(1). Определить четность перестановки .

Решение. Для определения четности перестановки вычислим в ней число «беспорядков», совпадающее по четности с числом инверсий. «Беспорядком» называется такое расположение чисел в последовательности , при котором большее число стоит впереди меньшего. Число 3 образует один «беспорядок» (стоит перед числом 2), число 5 образует 2 «беспорядка» (стоит перед числами 2 и 4). Перестановка нечетная, так как число «беспорядков» равно 3.

Задача 5(2). Определить четность перестановки .

Решение. В последовательности каждое число образует «беспорядок», следовательно, общее число «беспорядков» равно .

З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Определить четность перестановок.

5.1. . 5.2. . 5.3. . 5.4. .

Задача 6(1). Выяснить, входит ли произведение в определитель пятого порядка и с каким знаком.

Решение. Расположим сомножители в порядке возрастания первых индексов. Тогда вторые индексы образуют перестановку . Так как , то произведение входит со знаком минус.

Задача 6(2). Выяснить, входит ли произведение в определитель -го порядка и с каким знаком.

Решение. Первые индексы упорядочены, вторые образуют перестановку с числом беспорядков . Знак .

З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Выяснить, какие из приведенных ниже произведений входят в определители соответствующих порядков и с какими знаками.

6.1. . 6.2. .

6.3. . 6.4. .

Задача 7(1). Вычислить определитель .

Решение. Вычитая из второй, третьей и четвертой строк первую, умноженную на 2, 3 и 4 соответственно, получим:

.

Задача 7(2). Вычислить определитель .

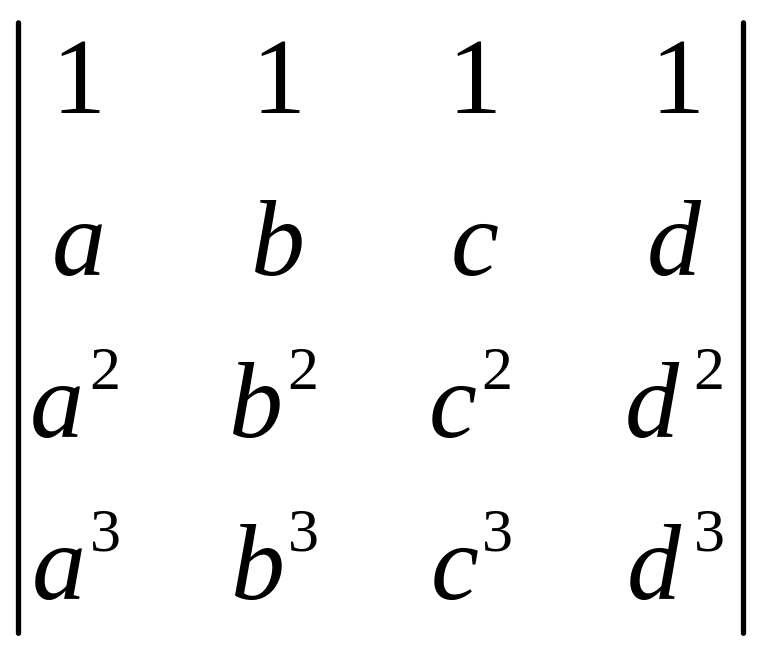Решение. Такой определитель называется определителем Вандермонда и обозначается . Он является многочленом шестой степени от переменных и , который обращается в нуль при равенстве любых двух из них. Это значит, что делится на все разности этих переменных и, следовательно, на их произведение . Так как степень этого произведения равна 6, то , где - некоторая константа. Сравнивая коэффициенты при одночлене (произведение элементов главной диагонали) в каждой из частей последнего равенства, получим , или .

З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Используя различные методы, вычислить определители.

7.1. . 7.2. . 7.3. . 7.4. .

Задача 8(1). Доказать линейную независимость системы функций .

Решение. Для доказательства линейной независимости системы функций достаточно показать, что определитель Вронского , где

.

Для нашей системы функций .

Задача 8(2). Доказать линейную независимость системы функций .

Решение. 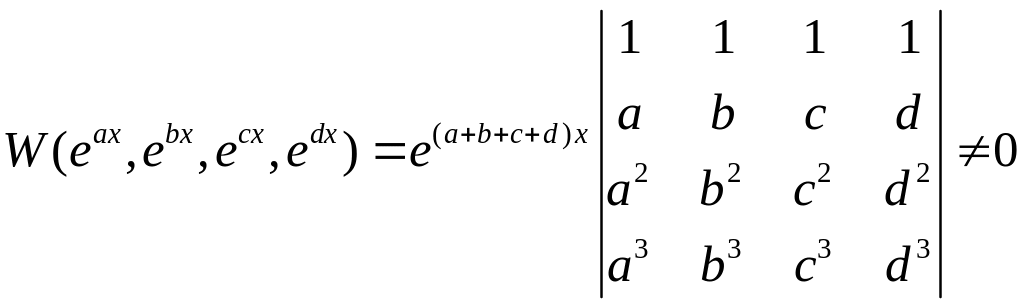, если попарно различны (см. задачу 7(2)).

З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Доказать линейную независимость следующих систем функций.

8.1. . 8.2. . 8.3. .

Ответы

1.1. . 1.2. 1. 1.3. 0. 1.4. . 1.5. . 1.6. 1. 1.7. .

2.1. 0. 2.2. 2. 2.3. .

2.4. .

4.1. . 4.2. .

4.3. . 4.4. .

В задачах 5.1.-5.4. в ответах приведено число «беспорядков»: 5.1. 2. 5.2. 10. 5.3 6. 5.4 .

6.1. Плюс. 6.2. Не является членом определителя (среди первых индексов нет 1, и дважды встречается число 2). 6.3. Минус. 6.4. .

7.1. 30. 7.2. 24. 7.3. . 7.4. .