Тема 3. Определители
Определитель квадратной матрицы второго порядка задается формулой:
.
Задача
1(1) Вычислить
определитель матрицы
.
Решение.
.
Задача
1(2) Вычислить
определитель матрицы
.
Решение.
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Вычислить определители следующих матриц второго порядка.
1.1.
.
1.2.
1.3.
.
1.4.
.
1.5.
.
1.6.
.
1.7.
Определитель матрицы третьего порядка вычисляется по формуле:
.
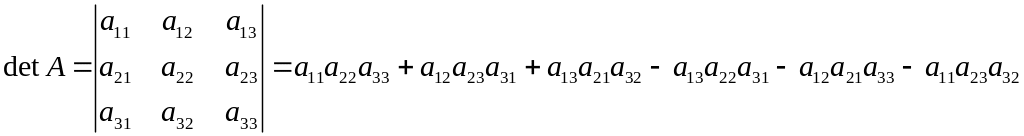Ч
тобы
запомнить эту формулу, построим
вспомогательную матрицу размера
,
полученную из матрицы
добавлением к ней справа ее первого и
второго столбцов. В этой матрице элементы,
стоящие на
главной диагонали матрицы
и на двух параллельных ей отрезках,
соединим сплошными линиями, а элементы,
стоящие на побочной диагонали и
параллельных ей отрезках, – пунктирными
(см. рис.).
Произведения матричных элементов, соединенных сплошной линией, входят в определитель матрицы со знаком плюс, а пунктирной – со знаком минус.
Задача
2(1). Вычислить
определитель третьего порядка
.
Решение.
.
Задача
2(1). Вычислить
определитель третьего порядка
.
Решение.
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Вычислить определители третьего порядка.
2.1.
.
2.2.
.
2.3.
.
2.4.
.
Основные свойства определителя
1.
,
где
– матрица, транспонированная к матрице
.
Из этого равенства следует, что любое утверждение, верное для столбцов определителя, верно и для строк определителя и обратно.
2. При умножении произвольной строки определителя на число, определитель умножается на это число.
3. Если строка определителя представлена в виде суммы двух строк, то определитель равен сумме двух определителей, у каждого из которых на месте данной строки стоит одно из слагаемых, а остальные строки прежние.
4. При перестановке двух строк определитель меняет знак.
5. Если строки определителя линейно зависимы, то определитель равен нулю.
6. Определитель не изменится, если к строке прибавить линейную комбинацию других строк определителя.
Задача
3(1). Доказать,
что определитель
равен нулю.
Решение.
,
так как
первый и третий столбцы пропорциональны.
Задача
3(2). Доказать,
что определитель
равен нулю, если
-
корни уравнения
.
Решение.
По формулам Виета коэффициент при
равен сумме корней уравнения
с обратным знаком, т.е.
.
Следовательно, строки определителя
линейно зависимы, так как их сумма равна
нулю.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Пользуясь свойствами определителя, доказать, что следующие определители равны нулю.
3.1.
.
3.2
.
3.3.
.
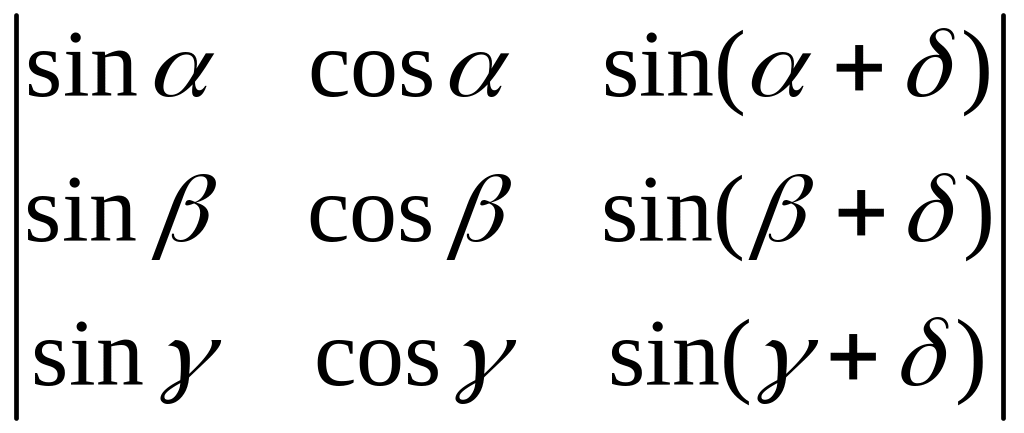3.4.
.
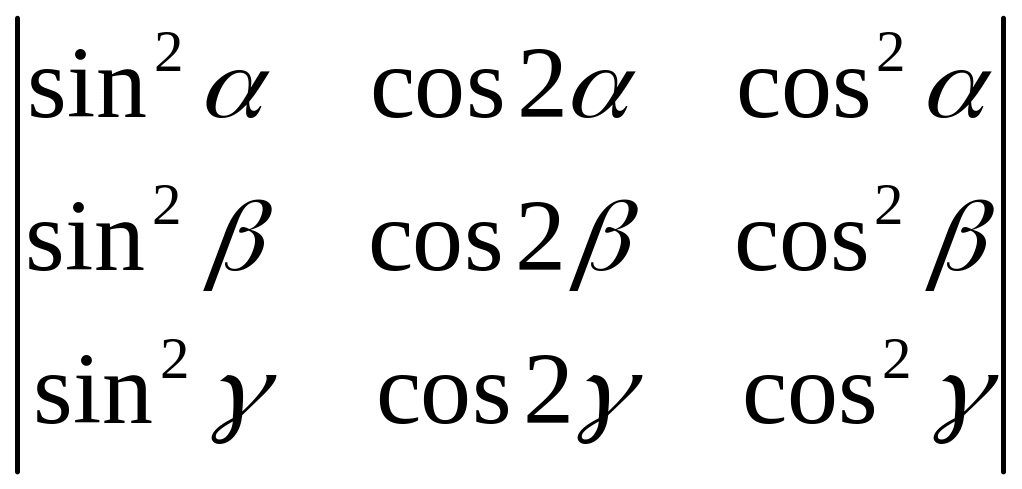Вычисление определителей
Метод
разложения
определителя по столбцу.
Пусть
– определитель матрицы, полученной из
матрицы
вычеркиванием строки c
номером
и столбца с номером
.
Алгебраическим дополнением элемента
квадратной матрицы
называется число
.
Формула разложения определителя по
элементам столбца имеет следующий вид:
.
Применение этого метода наиболее эффективно, если сначала, с помощью линейных преобразований строк матрицы, не меняющих определителя (см. свойство 6), обратить в ноль почти все элементы некоторого столбца, а затем применить формулу разложения по этому столбцу. Вычисление определителя значительно облегчается, если с помощью указанных выше преобразований удается привести матрицу к треугольному или блочно треугольному виду.
Задача 4(1). Вычислить определитель .
Решение.
.
Задача
4(2). Вычислить
определитель
.
Решение.
.
Задача
4(3). Вычислить
определитель
.
Решение.
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Используя различные методы, вычислить определители.
4.1.
.
4.2.
.
4.3.
.
4.4.
.