
- •Содержание
- •Введение
- •Тема 1. Линейные пространства
- •Подпространства
- •Линейная зависимость и независимость векторов
- •Ранг системы векторов
- •Базис, координаты, размерность
- •Сумма и пересечение подпространств
- •Тема 2. Линейные формы и линейные операторы
- •Линейные операторы
- •Тема 3. Определители
- •Основные свойства определителя
- •Вычисление определителей
- •Определители порядка
- •Тема 4. Алгебра матриц
- •Умножение матриц
- •Обратная матрица
- •Матричные уравнения
- •Тема 5. Системы линейных уравнений
- •Правило Крамера
- •Однородные системы
- •Неоднородные системы
- •Тема 6. Евклидовы пространства
- •Тема 7. Смена базиса Матрица перехода
- •Изменение матрицы линейного преобразования
- •Тема 8. Канонический вид матрицы линейного оператора Собственные векторы и собственные значения оператора
- •Диагональный вид матрицы оператора
- •Канонический вид матрицы оператора в случае комплексных корней характеристического уравнения
- •Самосопряженные операторы
- •Тема 9. Билинейные и квадратичные формы
- •Тема 10. Линии и поверхности второго порядка
- •Линейная алгебра в примерах и задачах
Ранг системы векторов
Рангом системы векторов называется максимальное число линейно независимых векторов этой системы.
Ранг системы
векторов
![]() пространства
пространства
![]() равен рангу системы столбцов, составленных
из координат этих векторов. Ранг системы
столбцов матрицы легко определяется,
если матрица имеет ступенчато-треугольный
вид (см. задачи 5(1) и 5(2)). Если матрица не
имеет специального вида, то с помощью
элементарных
преобразований строк,
сохраняющих линейные соотношения между
столбцами, её можно привести к
ступенчато-треугольному виду.
равен рангу системы столбцов, составленных
из координат этих векторов. Ранг системы
столбцов матрицы легко определяется,
если матрица имеет ступенчато-треугольный
вид (см. задачи 5(1) и 5(2)). Если матрица не
имеет специального вида, то с помощью
элементарных
преобразований строк,
сохраняющих линейные соотношения между
столбцами, её можно привести к
ступенчато-треугольному виду.
Элементарными преобразованиями строк матрицы (ЭПС) называются следующие операции над матрицей:
1) перестановка строк;
2) умножение строки на отличное от нуля число;
3) прибавление к строке другой строки, умноженной на произвольное число.
Задача
6. Найти
ранг системы векторов
 .
.
Решение.
Для определения
ранга матрицы приведем её с помощью ЭПС
к ступенчато-треугольному виду. Чтобы
объяснить порядок действий, обозначим
символом
![]() строчку с номером
строчку с номером
![]() преобразуемой матрицы.
преобразуемой матрицы.
В матрице после стрелки указаны действия над строками преобразуемой матрицы, которые необходимо выполнить для получения соответствующей строки новой матрицы.

 .
.
Очевидно, что первые два столбца полученной матрицы линейно независимы, третий является их линейной комбинацией, а четвертый не зависит от двух первых. Первый, второй и четвертый столбцы образуют максимальную линейно независимую подсистему, следовательно, ранг системы равен трем.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти ранг системы векторов
6.1.
 .
6.2.
.
6.2.
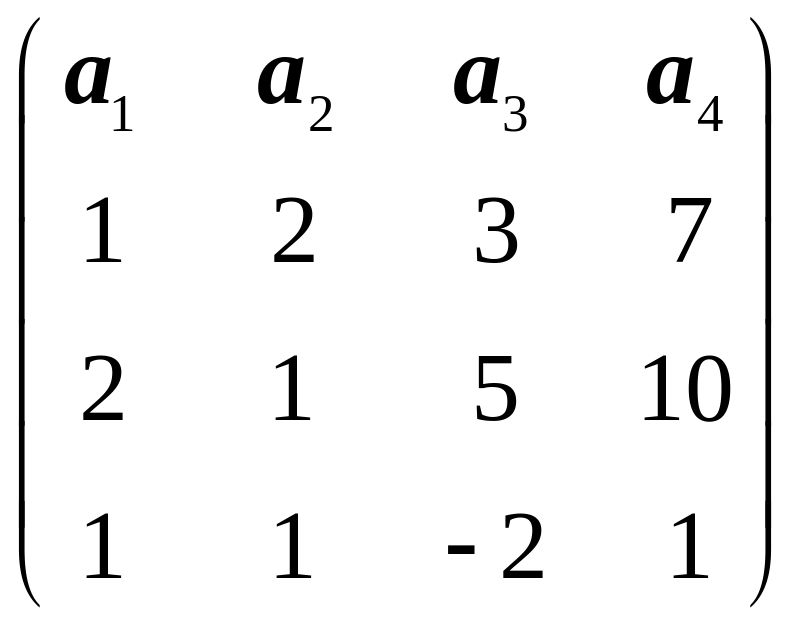 .
.
6.3.
 .
6.4.
.
6.4.
 .
.
Базис, координаты, размерность
Упорядоченная
система векторов
![]() образует
базис
пространства
,
если каждый вектор
образует
базис
пространства
,
если каждый вектор
![]() однозначно представим в виде:
однозначно представим в виде:
![]() .
.
Последнее
равенство называется разложением
вектора
![]() по базису, а коэффициенты разложения
-
координатами
вектора
в этом базисе. Размерность пространства
(обозначается
по базису, а коэффициенты разложения
-
координатами
вектора
в этом базисе. Размерность пространства
(обозначается
![]() )
равна числу базисных векторов. Каждый
вектор однозначно задается своими
координатами в фиксированном базисе.
Координаты векторов обладают свойством
линейности, т.е. при сложении векторов
их координаты складываются, а при
умножении вектора на число его координаты
умножаются на это число.
)
равна числу базисных векторов. Каждый
вектор однозначно задается своими
координатами в фиксированном базисе.
Координаты векторов обладают свойством
линейности, т.е. при сложении векторов
их координаты складываются, а при
умножении вектора на число его координаты
умножаются на это число.
Задача
7. В
пространстве
![]() всех матриц размера
выбрать некоторый базис и определить
координаты векторов в этом базисе.
всех матриц размера
выбрать некоторый базис и определить
координаты векторов в этом базисе.
Решение.
Каждая
матрица
![]() однозначно задается матричными элементами
однозначно задается матричными элементами
![]() .
Базис, в котором матричные элементы
являются координатами, состоит из матриц
.
Базис, в котором матричные элементы
являются координатами, состоит из матриц
![]() ,
у которых на месте
,
у которых на месте
![]() стоит единица, а на остальных местах
нули.
стоит единица, а на остальных местах
нули.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
В каждом из указанных пространств (подпространств) выбрать некоторый базис и определить координаты векторов в этом базисе.
7.1.
Пространства
геометрических векторов
![]() ,
,
![]() ,
,
![]() .
.
7.2. Пространство .
7.3.
Множество
![]() многочленов степени не выше п.
многочленов степени не выше п.
7.4.
Множество
всех векторов пространства
,
у которых координаты удовлетворяют
уравнению
![]() .
.
7.5.
Множество
всех векторов пространства
,
у которых координаты удовлетворяют
уравнению
![]() .
.
7.6. Множество всех векторов пространства , у которых координаты с четными номерами равны нулю.
7.7. Множество всех векторов пространства , у которых координаты с четными номерами равны между собой.
7.8. Множество всех векторов пространства , у которых координаты удовлетворяют уравнению .
7.9.
Множество
![]() четных многочленов степени не выше п.
четных многочленов степени не выше п.
7.10.
Множество
![]() нечетных многочленов степени не выше
п.
нечетных многочленов степени не выше
п.
7.11. Множество симметричных квадратных матриц порядка .
7.12. Множество кососимметричных квадратных матриц порядка .
Линейной
оболочкой
системы векторов
![]() называется множество всех линейных
комбинаций этих векторов. Линейная
оболочка (обозначается
называется множество всех линейных
комбинаций этих векторов. Линейная
оболочка (обозначается
![]() )
является минимальным подпространством,
содержащим систему векторов
.
Размерность
равна рангу
системы
,
а базисом является любая максимальная
линейно независимая подсистема.
)
является минимальным подпространством,
содержащим систему векторов
.
Размерность
равна рангу
системы
,
а базисом является любая максимальная
линейно независимая подсистема.
Задача 8. Найти размерность и базис линейной оболочки системы векторов
 .
.
Решение. Преобразуем с помощью ЭПС матрицу из координат векторов системы к ступенчато - треугольному виду.


 .
.
Столбцы
![]() последней матрицы линейно независимы,
а столбцы
последней матрицы линейно независимы,
а столбцы
![]() линейно выражаются через них. Следовательно,
векторы
образуют базис
линейно выражаются через них. Следовательно,
векторы
образуют базис
![]() ,
и
,
и
![]() .
.
Замечание.
Базис в
выбирается неоднозначно. Например,
векторы
![]() также образуют базис
.
также образуют базис
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти размерность и базис линейной оболочки системы векторов.
8.1.
.
8.2.
 .
.
8.3.
 .
8.4.
.
8.4.
 .
.
