Диагональный вид матрицы оператора

Матрица оператора диагональная тогда и только тогда, когда базис состоит из собственных векторов этого оператора. Такой базис называется собственным базисом оператора. Если корни характеристического уравнения оператора действительны и различны, то у оператора существует собственный базис, в котором его матрица имеет канонический диагональный вид.

Задача 2. Найти собственный базис оператора и его матрицу в этом базисе, если оператор задан матрицей .

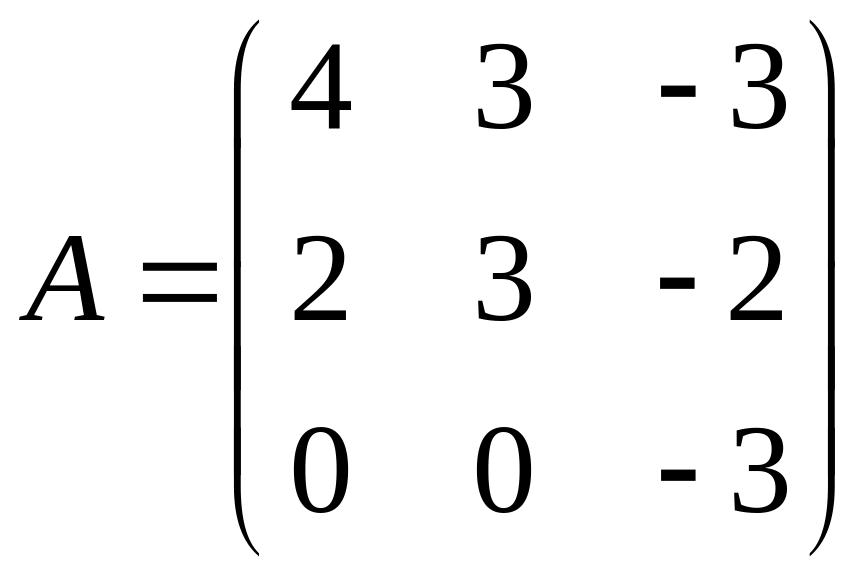Решение. Найдем корни характеристического уравнения оператора : Для каждого корня решим СЛАУ .

При система имеет решение .

При система имеет решение .

При система имеет решение .

Ответ: (Приводится матрица перехода к собственному базису и матрица оператора в этом базисе) .

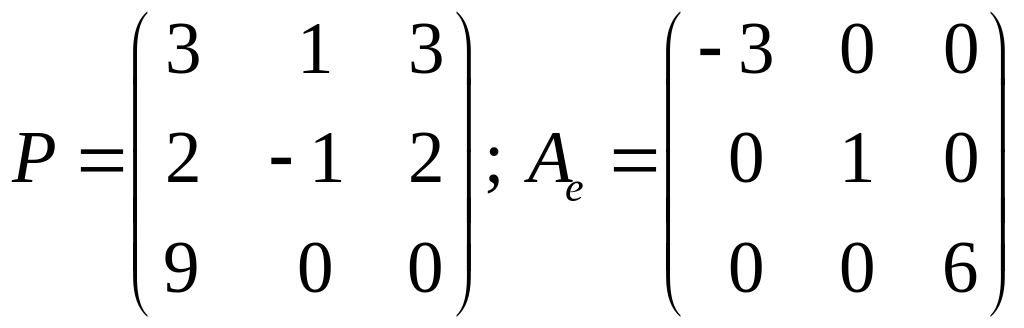З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Для операторов, заданных указанными матрицами, найти собственный базис и матрицу в этом базисе.

2.1. . 2.2. . 2.3. .

2.4. . 2.5. .

Канонический вид матрицы оператора в случае комплексных корней характеристического уравнения

В этом случае матрица оператора не приводится к диагональному виду, так как у оператора нет собственного базиса.

Пусть ( и – действительные векторы) – собственный вектор с собственным значением в пространстве над полем комплексных чисел. Линейная оболочка векторов и является инвариантным двумерным подпространством оператора , т.е. из условия . В базисе матрица ограничения оператора на подпространстве имеет вид

.

Если характеристическое уравнение оператора не содержит кратных корней, то матрица оператора в каноническом базисе имеет блочно диагональный вид, где на главной диагонали стоят действительные собственные значения оператора, а также блоки вида , соответствующие каждой паре сопряженных комплексных корней .

Задача 3. Найти канонический базис и матрицу оператора в этом базисе для оператора, заданного матрицей .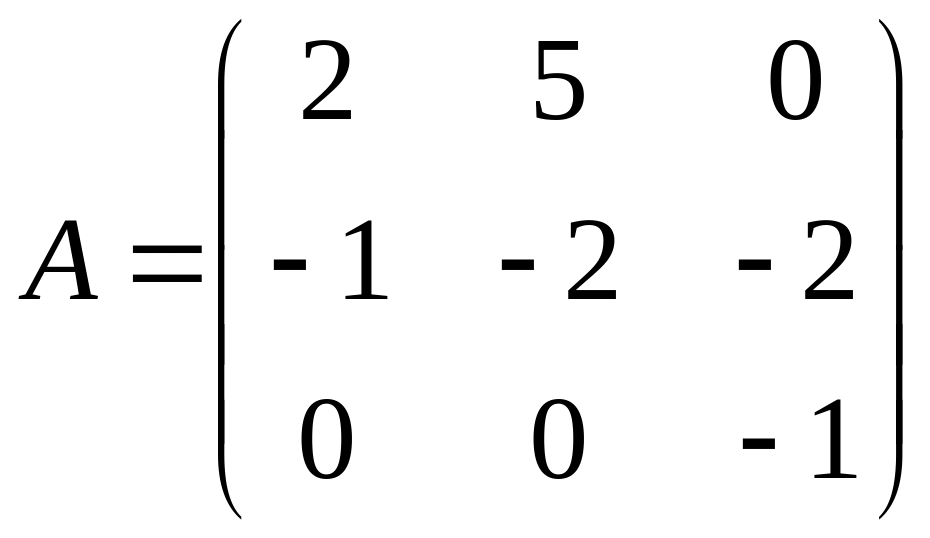

Решение. Найдем собственные значения.

Собственный вектор с собственным значением удовлетворяет системе: Выберем

Собственный вектор с собственным значением найдем, решив систему: Например .

Следовательно , где .

Ответ: .

З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Найти канонический базис и матрицу оператора в этом базисе для операторов, заданных следующими матрицами.

3.1. . 3.2. . 3.3. .

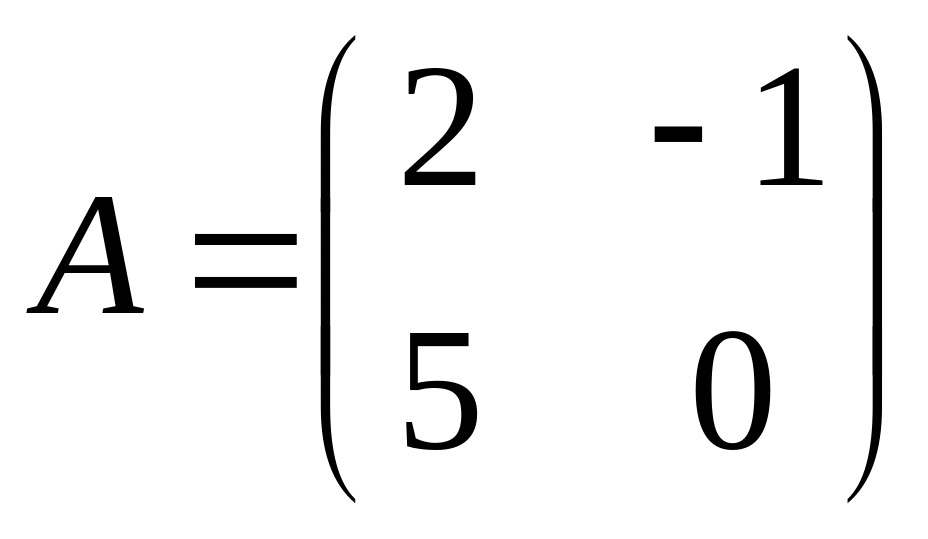3.4. . 3.5. .

Самосопряженные операторы

Оператор , действующий в евклидовом пространстве Е, называется самосопряженным, если . Матрица самосопряженного оператора в ОНБ симметрична. Все собственные значения самосопряженного оператора действительны, а собственные векторы с различными собственными значениями попарно ортогональны. У самосопряженного оператора существует собственный ОНБ.

Задача 4. Найти собственный ОНБ и матрицу оператора в этом базисе для оператора , заданного матрицей .

Решение. Так как ранг матрицы равен 1, то 0 является корнем характеристического уравнения кратности 2, т.е. . Корень найдем с помощью инварианта .

Собственные векторы с собственным значением удовлетворяют уравнению . Векторы образуют ортогональный базис этого собственного подпространства. Вектор , ортогональный векторам , является собственным вектором с собственным значением . Для того, чтобы получить собственный ОНБ пространства, надо пронормировать векторы .

Ответ: , .

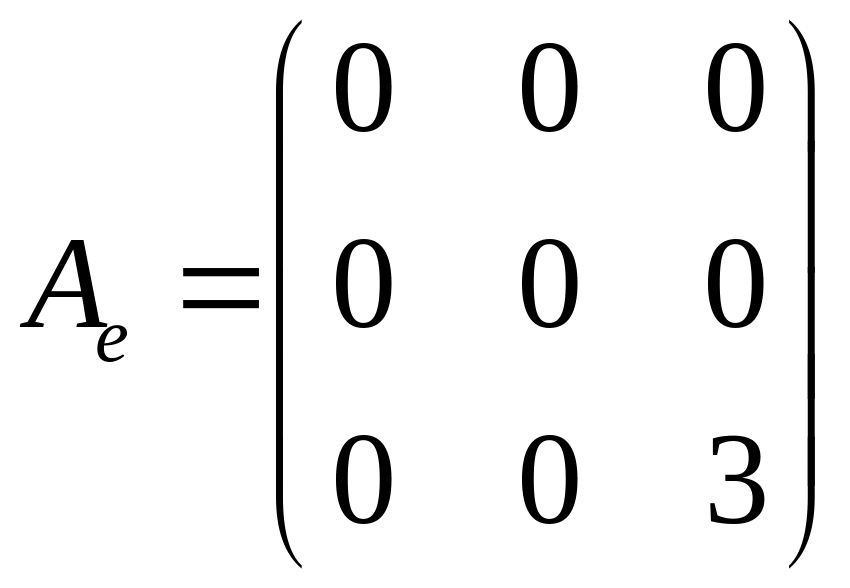З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Найти собственный ОНБ и матрицу оператора в этом базисе для операторов, заданных матрицами.

4.1. . 4.2. . 4.3. . 4.4. .

4.5. . 4.6. .

Задача 5. Найти собственный ОНБ для оператора ортогонального проецирования пространства на плоскость .

Решение. При ортогональном проецировании пространства на плоскость все векторы плоскости остаются неподвижными, т.е. являются собственными векторами с собственным значением 1, а вектор нормали переходит в нулевой вектор, т.е. является собственным вектором с собственным значением 0. Собственный ОНБ оператора (он неоднозначен) можно получить, если к любому ОНБ плоскости добавить вектор нормали единичной длины. Одна из матриц перехода имеет вид: , .

З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я

Найти собственный ОНБ для следующих операторов.

5.1. Оператор ортогонального проецирования пространства на плоскость .

5.2. Оператор симметрии пространства относительно плоскости .

5.3. Оператор ортогонального проецирования пространства на прямую .

5.4. Оператор симметрии пространства относительно прямой .

Ответы

1.1. Собственных векторов нет. 1.2. .

1.3. . 1.4. .

1.5. . 1.6. .

2.1. . 2.2. . 2.3. Нет.

2.4. . 2.5. .

3.1. 3.2.

3.3. 3.4.

3.5.

4.1. . 4.2. .

4.3. . 4.4. .

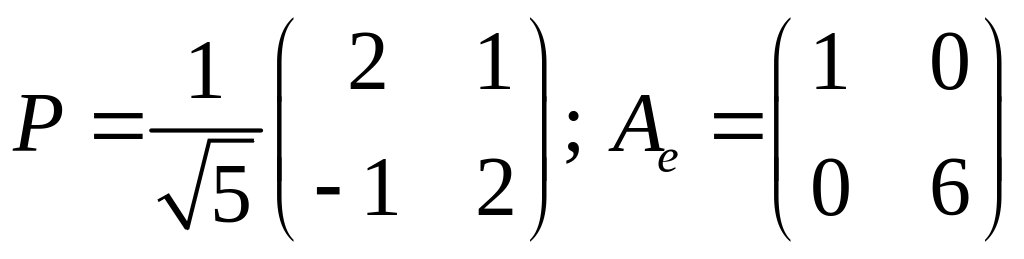4.5. , .

4.6. , .

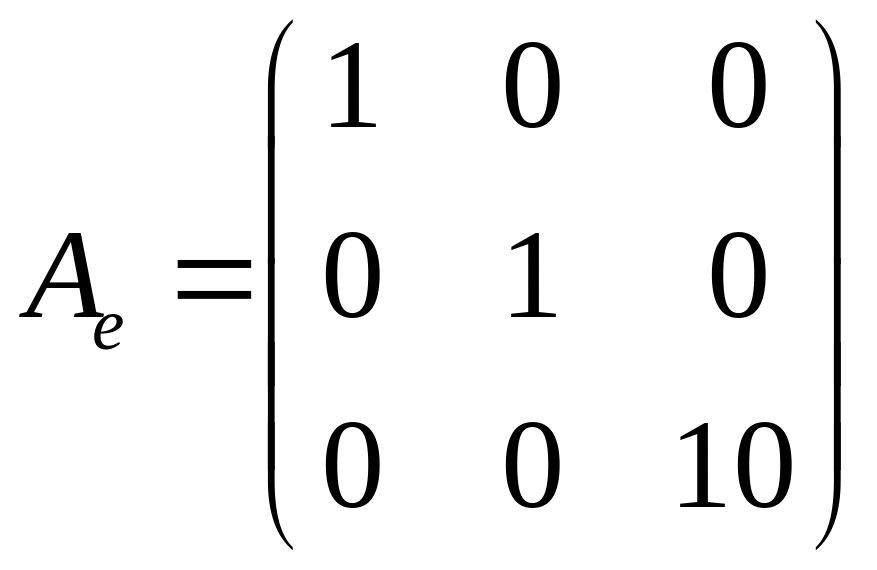5.1. , . 5.2. , .

5.3. , . 5.4. , .
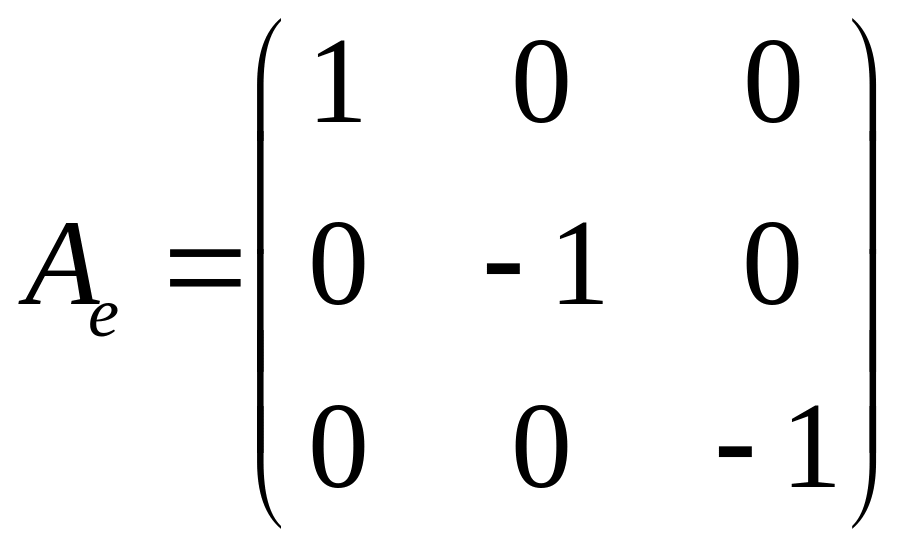