
- •Содержание
- •Введение
- •Тема 1. Линейные пространства
- •Подпространства
- •Линейная зависимость и независимость векторов
- •Ранг системы векторов
- •Базис, координаты, размерность
- •Сумма и пересечение подпространств
- •Тема 2. Линейные формы и линейные операторы
- •Линейные операторы
- •Тема 3. Определители
- •Основные свойства определителя
- •Вычисление определителей
- •Определители порядка
- •Тема 4. Алгебра матриц
- •Умножение матриц
- •Обратная матрица
- •Матричные уравнения
- •Тема 5. Системы линейных уравнений
- •Правило Крамера
- •Однородные системы
- •Неоднородные системы
- •Тема 6. Евклидовы пространства
- •Тема 7. Смена базиса Матрица перехода
- •Изменение матрицы линейного преобразования
- •Тема 8. Канонический вид матрицы линейного оператора Собственные векторы и собственные значения оператора
- •Диагональный вид матрицы оператора
- •Канонический вид матрицы оператора в случае комплексных корней характеристического уравнения
- •Самосопряженные операторы
- •Тема 9. Билинейные и квадратичные формы
- •Тема 10. Линии и поверхности второго порядка
- •Линейная алгебра в примерах и задачах
Изменение матрицы линейного преобразования
Пусть линейный оператор, отображающий пространство в себя.
Если
![]() и
и
![]() – матрицы линейного оператора
в базисах
и
соответственно, а
– матрица перехода от базиса
к базису
,
то выполняется соотношение
– матрицы линейного оператора
в базисах
и
соответственно, а
– матрица перехода от базиса
к базису
,
то выполняется соотношение
![]() .
.
Задача
5. Линейное
преобразование в исходном базисе задано
матрицей
 .
Найти его
матрицу
в базисе
:
.
Найти его
матрицу
в базисе
:
 .
.
Решение.
Матрица
перехода
![]() .
Вычислим матрицу
.
Для
.
Вычислим матрицу
.
Для
 матрица
матрица
 .
Матрицу
найдем по формуле
.
Матрицу
найдем по формуле
 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Линейное преобразование в исходном базисе задано матрицей . Найти его матрицу в базисе .






Ответы
1.1.
 1.2.
1.2.
 1.3.
1.3.

1.4.
 1.5.
1.5.

2.1. Поменяются местами две строки. 2.2. Поменяются местами два столбца. 2.3. Строки матрицы будут записаны в обратном порядке. 2.4. Столбцы матрицы будут записаны в обратном порядке. 2.5. Матрица отразится симметрично относительно своего центра.
3.1.
 .
3.2.
.
3.2.
 .
3.3.
.
3.3.
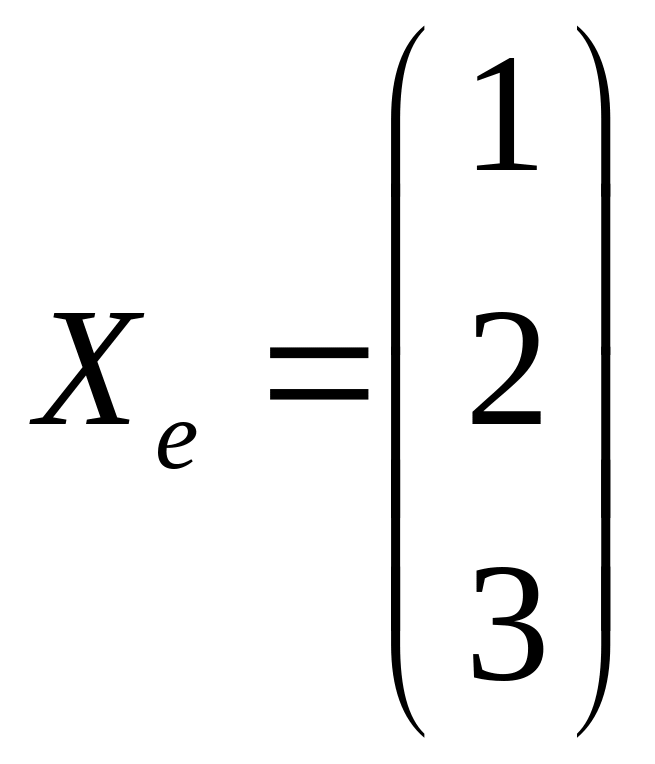 .
3.4.
.
3.4.
 .
.
В задачах 4.1-4.3. в ответах приводятся строки из коэффициентов форм в базисе .
4.1.
![]() 4.2.
4.2.
![]() 4.3.
4.3.
![]() .
4.4.
.
4.4.
![]() .
.
5.1.
 5.2.
5.2.
 5.3.
5.3.
 5.4.
5.4.

5.5.
 5.6.
5.6.

Тема 8. Канонический вид матрицы линейного оператора Собственные векторы и собственные значения оператора
Пусть
– линейный оператор, переводящий
пространство
в себя. Ненулевой вектор
,
удовлетворяющий равенству
![]() ,
называется собственным
вектором оператора
,
а число
соответствующим ему собственным
значением.
В произвольном базисе
столбец координат
собственного вектора является ненулевым
решением СЛАУ
,
называется собственным
вектором оператора
,
а число
соответствующим ему собственным
значением.
В произвольном базисе
столбец координат
собственного вектора является ненулевым
решением СЛАУ
![]() Эта система имеет нетривиальное решение
тогда и только тогда, когда
Эта система имеет нетривиальное решение
тогда и только тогда, когда
![]() .
Собственные значения
являются корнями этого уравнения,
которое называется характеристическим
уравнением
матрицы
.
Характеристическое уравнение не меняется
при смене базиса, т.е. зависит только от
оператора
.
Коэффициенты этого уравнения являются
инвариантами
матрицы оператора
.
.
Собственные значения
являются корнями этого уравнения,
которое называется характеристическим
уравнением
матрицы
.
Характеристическое уравнение не меняется
при смене базиса, т.е. зависит только от
оператора
.
Коэффициенты этого уравнения являются
инвариантами
матрицы оператора
.
Задача
1(1). Найти
собственные векторы оператора
,
заданного матрицей
 .
.
Решение.
Составим характеристическое уравнение
![]() .
.
 .
Корни этого уравнения
.
Корни этого уравнения
![]() являются собственными значениями
оператора
.
являются собственными значениями
оператора
.
Решим
СЛАУ
![]() для каждого собственного значения. При
для каждого собственного значения. При
![]() СЛАУ эквивалентна уравнению
СЛАУ эквивалентна уравнению
![]() с общим решением
с общим решением
![]() .
При
.
При
![]() получим уравнение
получим уравнение
![]() с общим решением
с общим решением
![]()
Ответ:
 .
.
Задача
1(2). Найти
собственные векторы оператора
,
заданного матрицей
 .
.
Решение.
Корни характеристического уравнения
![]() комплексные
комплексные
![]() ,
поэтому действительных собственных
векторов нет.
,
поэтому действительных собственных
векторов нет.
Задача
1(3). Найти
собственные векторы оператора
,
заданного матрицей
 .
.
Решение.
Характеристическое
уравнение
![]() имеет вид:
имеет вид:
 .
.
Все собственные значения оператора равны 1.
СЛАУ
при
эквивалентна уравнению
![]() с общим решением
с общим решением
![]() .
Эти решения образуют подпространство
размерности 2, состоящее из собственных
векторов с собственным значением 1
(собственное
подпространство).
.
Эти решения образуют подпространство
размерности 2, состоящее из собственных
векторов с собственным значением 1
(собственное
подпространство).
Ответ:
 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти собственные векторы операторов, заданных следующими матрицами:
1.1.
 .
1.2.
.
1.2.
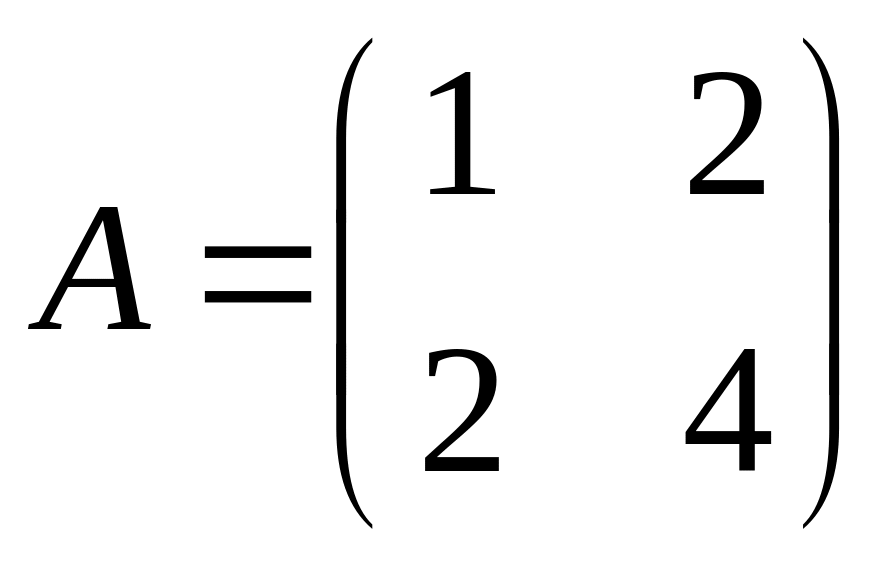 .
1.3.
.
1.4.
.
1.3.
.
1.4.
 .
.
1.5. .
1.6.
.
1.6.
 .
.
