
- •Содержание
- •Введение
- •Тема 1. Линейные пространства
- •Подпространства
- •Линейная зависимость и независимость векторов
- •Ранг системы векторов
- •Базис, координаты, размерность
- •Сумма и пересечение подпространств
- •Тема 2. Линейные формы и линейные операторы
- •Линейные операторы
- •Тема 3. Определители
- •Основные свойства определителя
- •Вычисление определителей
- •Определители порядка
- •Тема 4. Алгебра матриц
- •Умножение матриц
- •Обратная матрица
- •Матричные уравнения
- •Тема 5. Системы линейных уравнений
- •Правило Крамера
- •Однородные системы
- •Неоднородные системы
- •Тема 6. Евклидовы пространства
- •Тема 7. Смена базиса Матрица перехода
- •Изменение матрицы линейного преобразования
- •Тема 8. Канонический вид матрицы линейного оператора Собственные векторы и собственные значения оператора
- •Диагональный вид матрицы оператора
- •Канонический вид матрицы оператора в случае комплексных корней характеристического уравнения
- •Самосопряженные операторы
- •Тема 9. Билинейные и квадратичные формы
- •Тема 10. Линии и поверхности второго порядка
- •Линейная алгебра в примерах и задачах
Матричные уравнения
1.
Уравнения вида
![]() и
и
![]() .
Если
невырожденная матрица (
),
то решение первого уравнения дается
формулой
.
Если
невырожденная матрица (
),
то решение первого уравнения дается
формулой
![]() ,
а второго формулой
,
а второго формулой
![]() .
.
2.
Уравнения вида
![]() решаются аналогично, при условии, что
и
невырожденные матрицы. Решение дается
формулой
решаются аналогично, при условии, что
и
невырожденные матрицы. Решение дается
формулой
![]() .
.
3.
Уравнения п.п. 1) и 2) в случае вырожденности
соответствующих матриц, а также уравнения
вида
![]() сводятся
к решению систем линейных уравнений
относительно элементов матрицы
.
сводятся
к решению систем линейных уравнений
относительно элементов матрицы
.
Задача
7(1). Решить
матричное уравнение
 .
.
Решение.
 .
.
Задача
7(2). Решить
матричное уравнение
 .
.
Решение.
 .
.
Задача
7(3). Решить
матричное уравнение
 .
.
Решение.
Так как
матрица
 вырождена, а матрица
вырождена, а матрица
 невырожденная,
то уравнение не имеет решений.
невырожденная,
то уравнение не имеет решений.
Задача
7(4). Решить
матричное уравнение
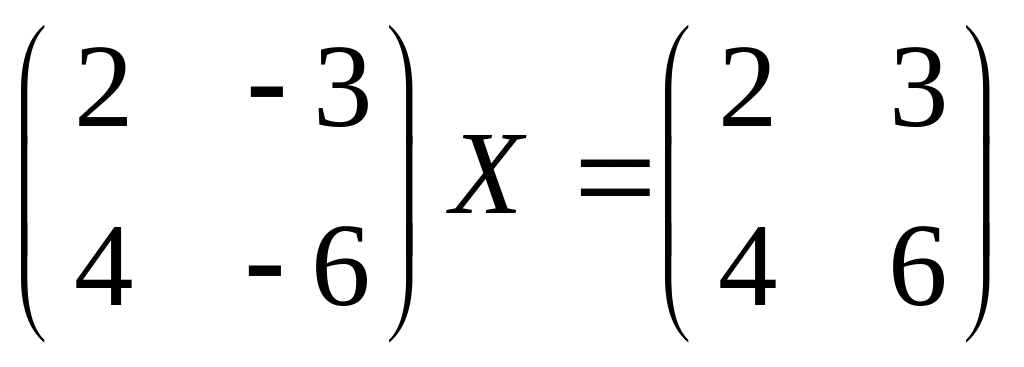 .
.
Решение.
Определитель матрицы
 равен нулю, поэтому она не имеет обратной
матрицы. Это уравнение сведем к системе
уравнений относительно матричных
элементов матрицы
.
Имеем:
равен нулю, поэтому она не имеет обратной
матрицы. Это уравнение сведем к системе
уравнений относительно матричных
элементов матрицы
.
Имеем:
 .
.
Следовательно,
 ,
где
,
где
![]() и
любые числа.
и
любые числа.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Решить матричные уравнения.
7.1.
 .
7.2.
.
7.2.
 .
.
7.3.
 .
7.4.
.
7.4.
 .
.
Ответы
1.1.
 .
1.2.
.
1.2.
 .
1.3.
.
1.3.
 .
1.4.
.
1.4.
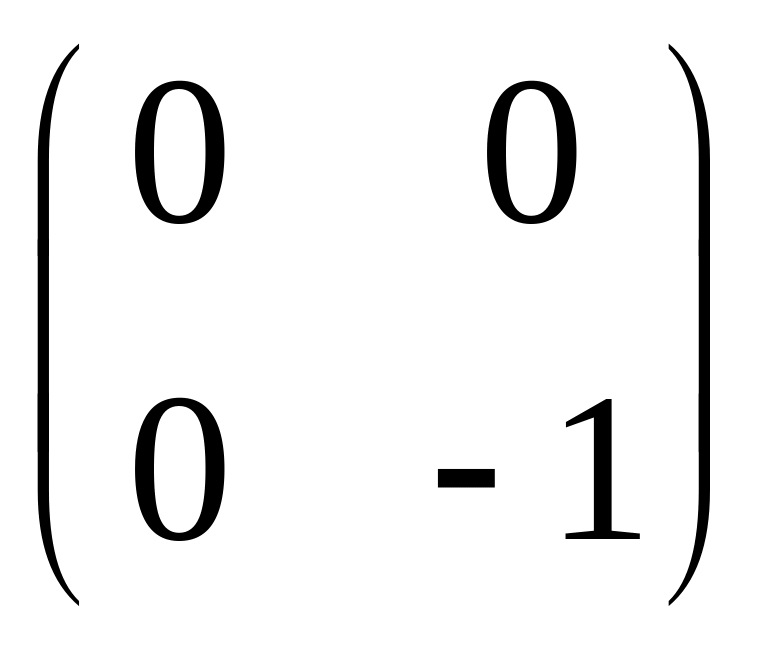 .
.
2.1.
 .
2.2.
.
2.3.
.
2.2.
.
2.3.
 .
2.4.
.
2.4.
 .
.
3.1.
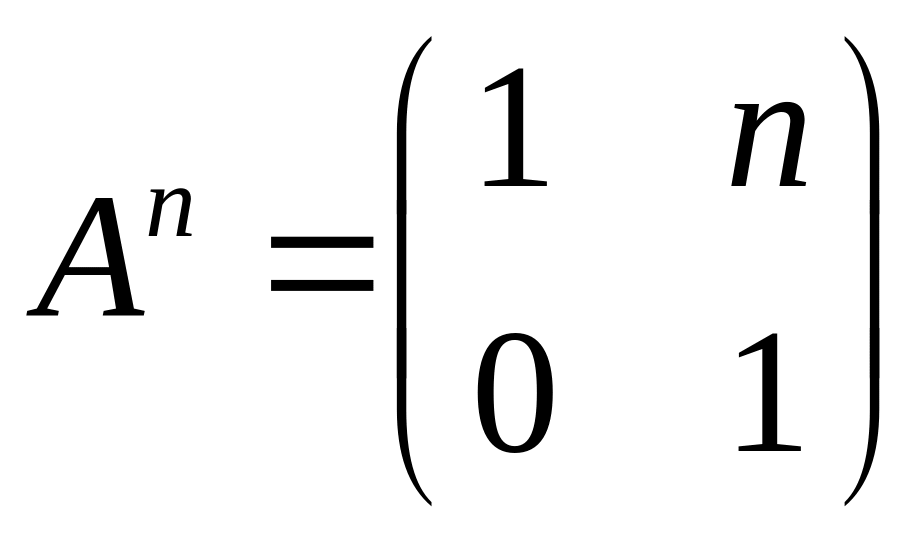 .
3.2.
.
3.2.
 .
3.3.
.
3.3.
 .
.
3.4.
 .
.
4.1.
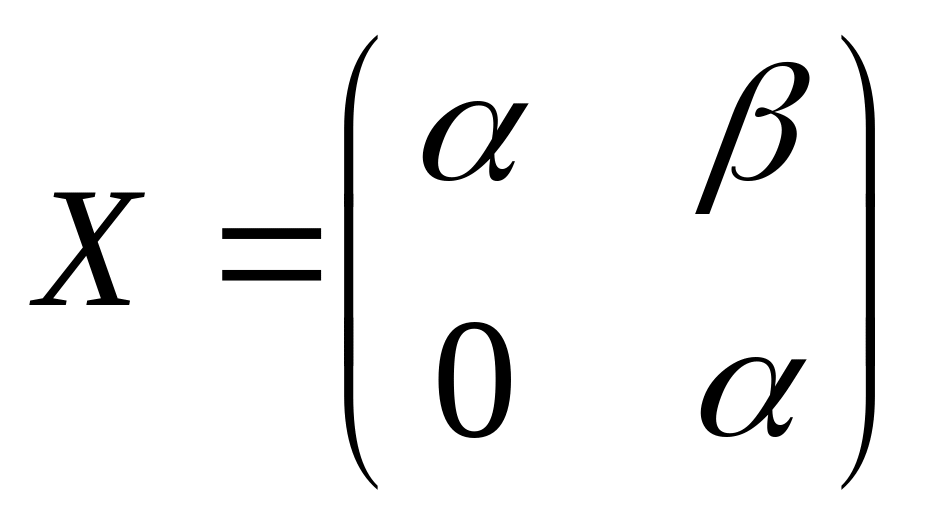 .
4.2.
.
4.2.
 .
4.3.
.
4.3.
 .
.
4.4.
 .
.
5.1.
 .
5.2.
.
5.2.
 .
5.3.
.
5.3.
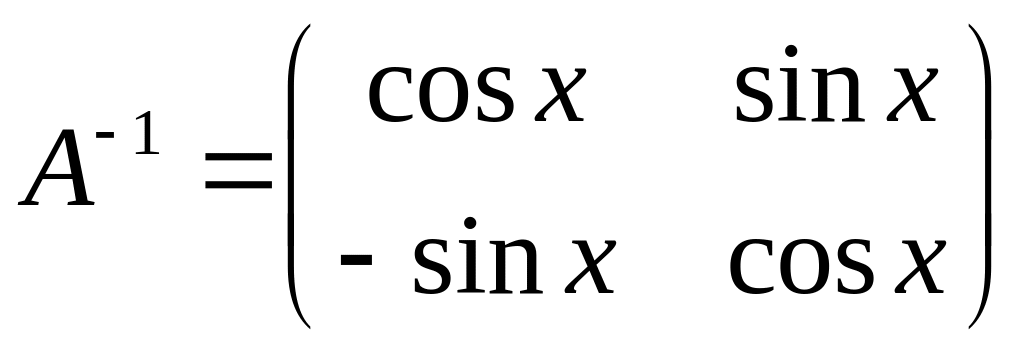 .
.
5.4.
 .
5.5.
.
5.5.
 .
.
6.1.
 .
6.2.
.
6.2.
 .
.
7.1.
 .
7.2.
.
7.2.
 .
7.3.
.
7.3.
 .
7.4. Нет
решений.
.
7.4. Нет
решений.
Тема 5. Системы линейных уравнений
Система
![]() линейных алгебраических уравнений с
неизвестными (ниже СЛАУ или система)
имеет следующий вид:
линейных алгебраических уравнений с
неизвестными (ниже СЛАУ или система)
имеет следующий вид:
 или,
в матричной записи,
или,
в матричной записи,
![]() ,
,
где
![]() – основная
матрица
системы,
– столбец переменных,
– основная
матрица
системы,
– столбец переменных,
![]() – столбец свободных членов. Матрица
– столбец свободных членов. Матрица
![]() ,
полученная из матрицы
добавлением столбца свободных членов
,
называется расширенной
матрицей
системы.
,
полученная из матрицы
добавлением столбца свободных членов
,
называется расширенной
матрицей
системы.
Правило Крамера
Пусть
СЛАУ
квадратная (число уравнений равно числу
неизвестных) и
.
Тогда система имеет единственное
решение, которое определяется по формуле
![]() ,
где
,
где
![]()
определитель матрицы, полученной из
матрицы
заменой
-
го столбца столбцом свободных членов
.
определитель матрицы, полученной из
матрицы
заменой
-
го столбца столбцом свободных членов
.
Задача 1(1). Решить по правилу Крамера систему уравнений
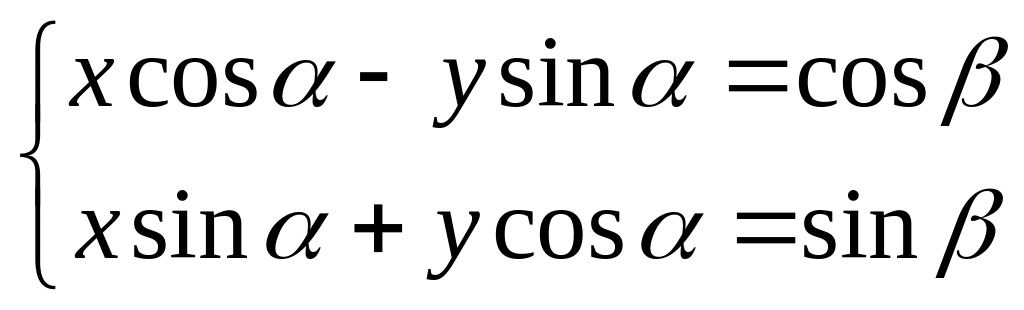 .
.
Решение. Расширенная матрица системы имеет следующий вид:
 .
.
Вычислим
определители
![]() .
.
 ,
,
 ,
,
 .
.
Таким
образом
![]() .
.
Задача
1(2). Решить
по правилу Крамера систему уравнений
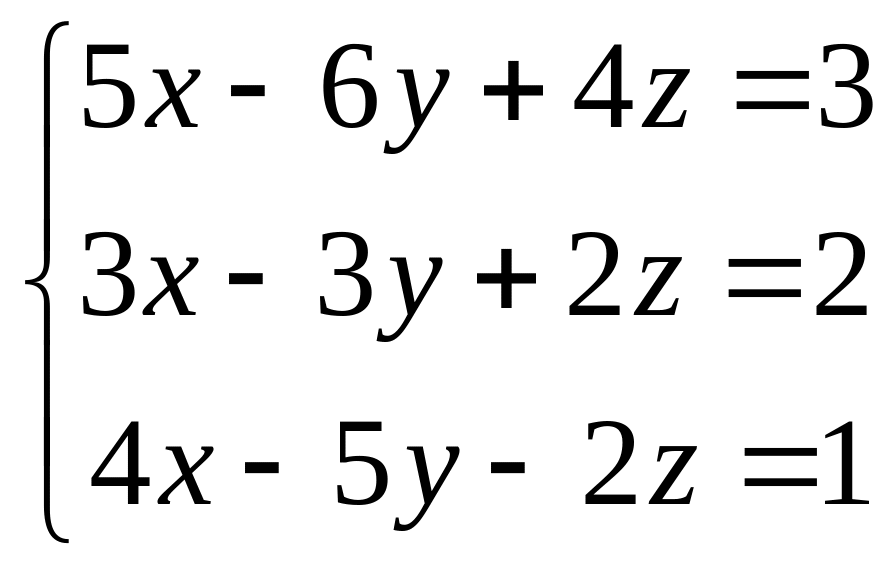 .
.
Решение.
Расширенная матрица системы
имеет вид
 .
.
 ,
,
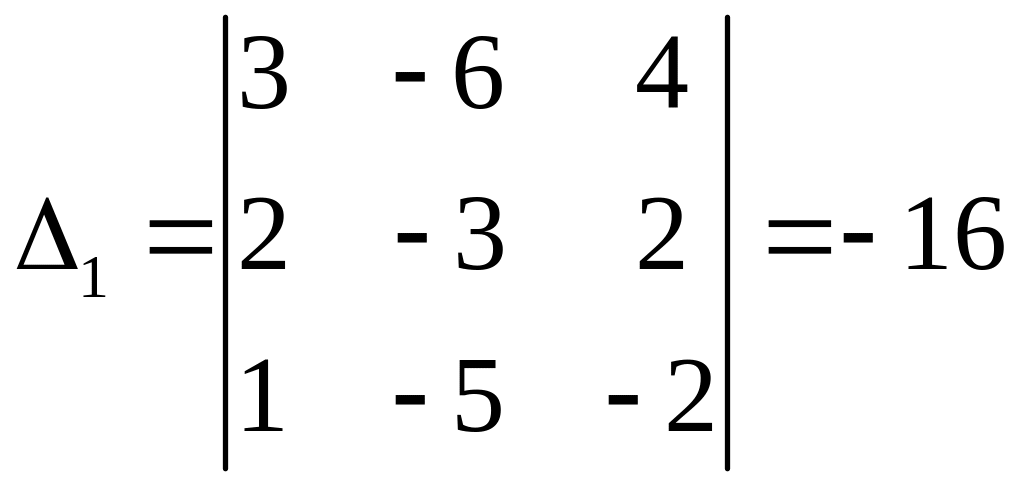 ,
,
 ,
,
 .
.
Ответ:
![]() .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Решить системы уравнений по правилу Крамера.
1.1.
 .
1.2.
.
1.2.
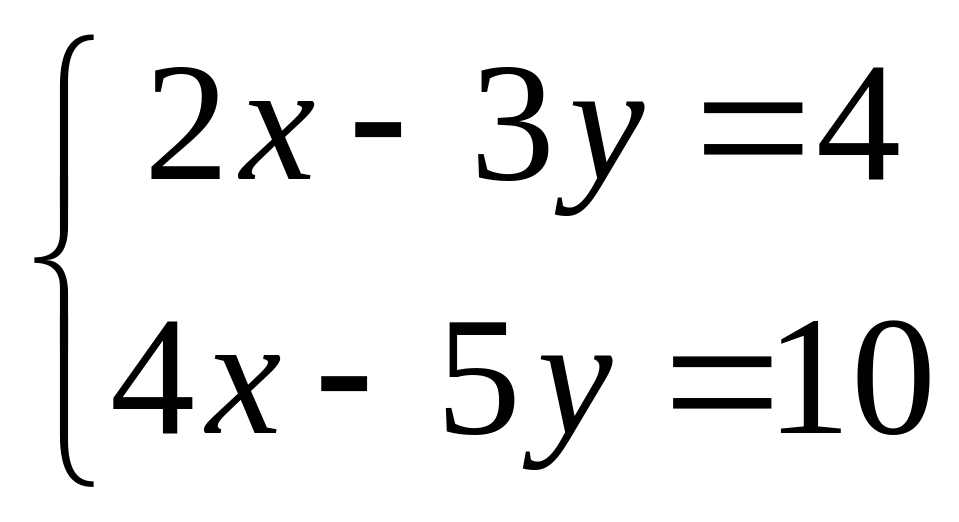 .
.
1.3.
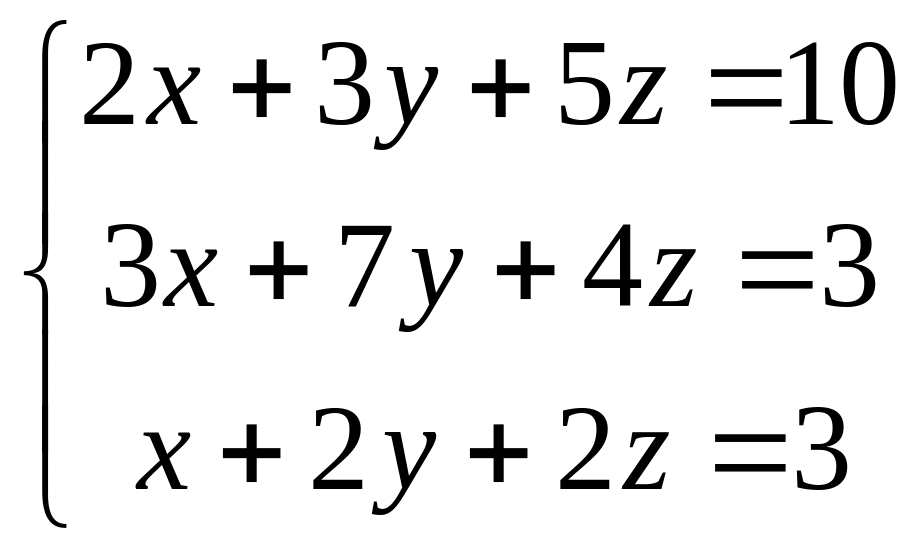 .
1.4.
.
1.4.
 .
.
Однородные системы
СЛАУ
![]() называется однородной.
называется однородной.
Однородная система всегда совместна, так как она имеет тривиальное (нулевое) решение. Однородная СЛАУ имеет нетривиальные решения, если ранг матрицы меньше числа неизвестных.
Выберем
![]() линейно независимых столбцов матрицы
,
где
линейно независимых столбцов матрицы
,
где
![]() .
Соответствующие этим столбцам переменные
называются базисными, а остальные
переменные - свободными. Каждое
решение системы однозначно задается
набором свободных переменных. Множество
всех решений однородной системы образует
подпространство
размерности
.
Соответствующие этим столбцам переменные
называются базисными, а остальные
переменные - свободными. Каждое
решение системы однозначно задается
набором свободных переменных. Множество
всех решений однородной системы образует
подпространство
размерности
![]() .
Базис пространства
,
состоящий из
линейно независимых решений, называется
фундаментальной системой решений
(ФСР). Для получения ФСР достаточно
задать
линейно независимых наборов свободных
переменных и найти соответствующие им
решения системы. Пусть
.
Базис пространства
,
состоящий из
линейно независимых решений, называется
фундаментальной системой решений
(ФСР). Для получения ФСР достаточно
задать
линейно независимых наборов свободных
переменных и найти соответствующие им
решения системы. Пусть
![]() ФСР. Общее
решение
ФСР. Общее
решение
![]() однородной системы представимо в виде:
однородной системы представимо в виде:
![]() .
.
Задача 2. Найти ФСР и общее решение системы уравнений
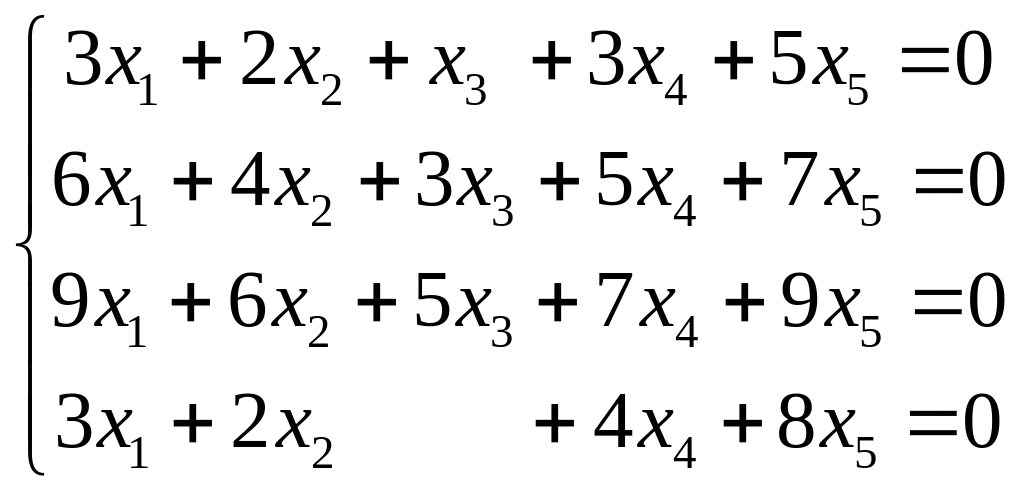 .
.
Решение. Приведем матрицу с помощью линейных преобразований строк к ступенчато треугольному виду.
![]()
 .
.
Ранг
системы равен двум. Пусть
![]() – базисные, а
– свободные переменные. Перенеся
свободные переменные в правую часть
уравнений, запишем систему в следующем
виде:
– базисные, а
– свободные переменные. Перенеся
свободные переменные в правую часть
уравнений, запишем систему в следующем
виде: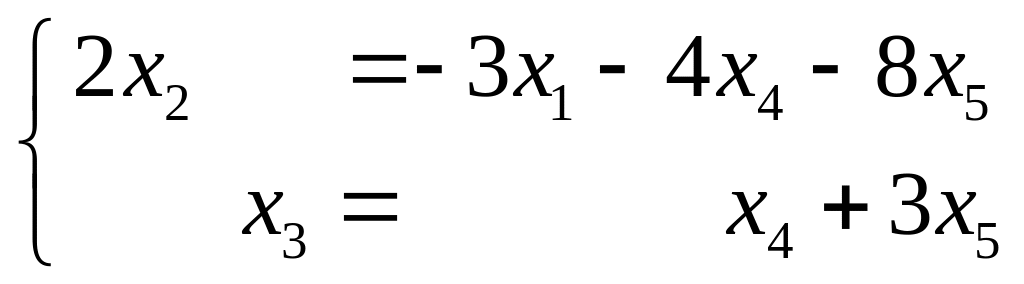 .
.
ФСР
зададим следующими наборами свободных
переменных:
 ;
;
 ;
;
 .
.
Общее
решение
![]() .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти ФСР и общее решение систем уравнений.
2.1.
 .
2.2.
.
2.2.
 .
.
2.3.
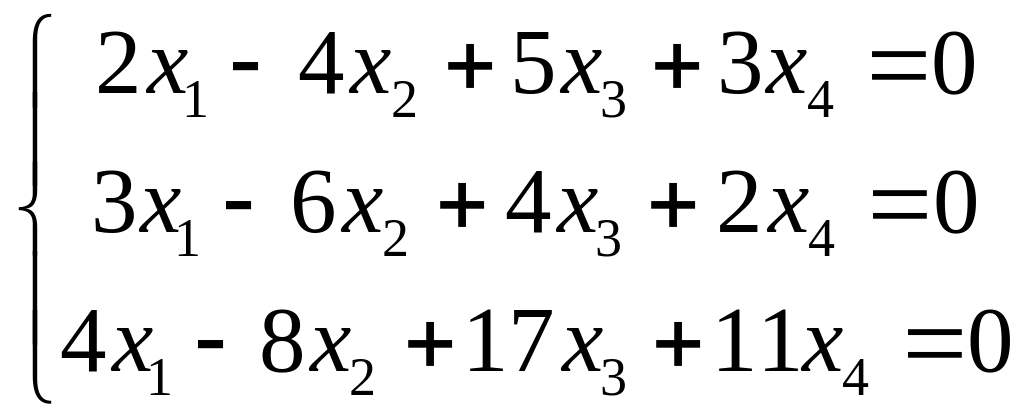 .
2.4.
.
2.4.
 .
.
2.5.
 .
.
