47) Основные понятия и определение определенного интеграла.
Рассмотрим
произвольную функцию
,
которая определена и непрерывна на
отрезке
.
Разобъем отрезок
на 
частей
(не обязательно равных) точками
которые
не совпадают. Получаем, что отрезок
есть
объединение полуинтервалов открытых
справа 
, 
и
отрезка 
,
т.е.
(эти
полуинтервалы 
и
отрезок 
будем
называть множествами).
Возьмем
из каждого множества 
произвольную
точку 
и
составим следующую сумму:
где 
--
длина (мера) полуинтервала 
(множества
).
Определение. Предел
от суммы 
при 
,
если он существует и конечен,
называется определенным
интегралом от
функции
в
пределах от 
до 
и
обозначается:
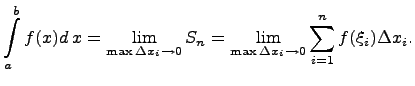
Если существует определенный интеграл от функции , то в этом случае функция называется интегрируемой на отрезке .
Для интегрируемости функции на отрезке достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
Если функция непрерывна на , то от нее существует неопределенный интеграл
и имеет место формула
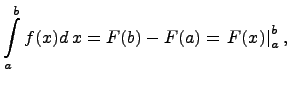
т.е. определенный интеграл от непрерывной функции равен разности значений первообразной функции (или неопределенного интеграла) при верхнем и нижнем пределах.
Формула
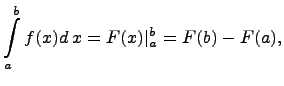
называется формулой Ньютона-Лейбница.
СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Будем предполагать, что все рассматриваемые ниже функции интегрируемы на заданных промежутках.
Свойство
1. 
(6)
Для
доказательства составим интегральные
суммы (3) в обоих случаях с теми же точками
деления. Они будут отличаться только
знаком за счет знаков 
:
слева 
>0,
справа
<0.
Значит, в пределе получится нужное
равенство.
Свойство
2. 
(7)
В этом случае отрезок интегрирования равен нулю и интегральная сумма – тоже.
Свойство
3. Постоянный
множитель можно выносить за знак
определенного интеграла: если 
,
то
(8)
Доказательство:
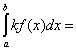(см.(4))
= 
=
=
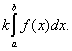
Свойство 4. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от этих функций:
(9)
Доказательство предлагается провести самостоятельно, используя равенство (4).
Свойство 5. Если отрезок [a, b] разбит точкой с на две части [a, c] и [c, b], то
(10)
Доказательство. Составим
интегральную сумму для 
на
[a, b].
Так как предел этих сумм не зависит от
способа разбиения [a, b]
на части, то рассмотрим только те
разбиения, в которых точка с входит в
качестве точки деления. Тогда
48 Теорема существования определённого интеграла. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема по этому отрезку.
Примем это утверждение без доказательства, поясним только его смысл. Интегрируемость функции означает существование конечного предела последовательности интегральных сумм, т.е. такого числа , что для любого найдётся такое число , что как только разбиение отрезка удовлетворяет неравенству , то, независимо от выбора точек выполняется неравенство. Требование непрерывности f(x) достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на [a,b] при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если f(x) неограничена на [a,b], то она неограничена на каком-либо [xi-1 , xi], т.е. на этом отрезке можно найти такую точку , что слагаемое , а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа).