30 Предел и непрерывность функций нескольких переменных

Пусть функция z = (х, у) определена в области D плоскости XOY, а т. лежит в области D (см. рис. 11.4).

О: Число А называется пределом функции f(x, у) при стремлении т. М(х, у) к т. если для любого числа >0 найдется такое число >0, что для всех т. М(х, у)  за исключением, быть может, т. справедливо неравенство

Основные теоремы о пределах функции одной переменной (см. разд. 7.5) справедливы и для функций двух и большего числа переменных.

О: Функция z = (х, у) называется непрерывной в т.  если: 1) она определена в т. и ее окрестности,

2)

О: Функция z =f(x, у) называется непрерывной на некотором множестве Е D, если она непрерывна в каждой точке этого множества.

О: Точка называется точкой разрыва функции (М), если в ней нарушено хотя бы одно из условий 1), 2). Точки разрыва могут быть изолированными, могут образовывать линии разрыва.

Примеры: 1)

Функция не определена в точках, в которых знаменатель обращается в нуль у = х — линия разрыва

2)

 т. — точка разрыва

Для функции трех и более переменных определения предела и непрерывности аналогичны.

О: Число А называется пределом функции у = (М) при стремлении т. к т.если  для любого > 0 существует такое > 0, что из условия

следует

31. Частные производные функции двух переменных

Рассмотрим функцию двух переменных  .

Зафиксируем значение одного из ее аргументов, например  , положив  . Тогда функция   есть функция одной переменной  .

Пусть она имеет производную в точке  :

.

Данная производная называется частной производной (или частной производной первого порядка) функции   по   в точке   и обозначается одним из следующих символов:  ;  ;  ;  .

Разность   называется частным приращением по   функции   в точке   и обозначается символом  :

.

Учитывая приведенные обозначения, можно записать

.

Аналогично определяются и обозначаются частное приращение функции   по   и частная производная по   в точке  : _ю,, .

Значение частной производной зависит от точки  , в которой она вычисляется. Поэтому частная производная функции двух переменных  , вообще говоря, есть функция точки  , т.е. также является функцией двух переменных   и  .

Все правила и формулы дифференцирования, выведенные для производных функций одной переменной, сохраняются для частных производных функции двух переменных.

Однако следует помнить, что при нахождении частной производной по какому-либо аргументу второй аргумент считается постоянным.

Заметим, что частные производные функции являются функциями тех же переменных. Эти функции, в свою очередь, могут иметь частные производные, которые называются вторыми частными производными (или частными производными второго порядка) исходной функции.

Например, функция   имеет четыре частных производных второго порядка, которые обозначаются следующим образом:

;  ;

;  .

При этом частные производные   и   называются смешанными частными производными.

Обратите внимание на то, что  . Данный результат не случаен, так как имеет место следующая теорема.

Теорема 7.1. Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

32. Полный дифференциал функции нескольких переменных. Частные производные высших порядков

 Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

Пусть задана функция   . Если аргументу   сообщить приращение  , а аргументу   – приращение  , то функция  получит приращение  , которое называется полным приращением функции и определяется формулой:  .

Функция  , полное приращение   которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно   и  , и величины бесконечно малой высшего порядка относительно  ):  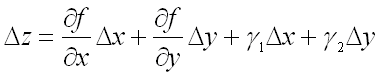, где   и   стремятся к нулю, когда   и   стремятся к нулю (т.е. когда  ), называется дифференцируемой в данной точке.

Линейная (относительно   и  ) часть полного приращения функции называется полным дифференциалом и обозначается  :  , где   и   – дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям   и  .

Частные производные от частных производных первого порядка называются частными производными второго порядка. Для функции двух переменных   их четыре:

33. Производные сложных функций.

О. Переменная z называется сложной функцией от независимых переменных х,у, t ,… если она задана посредством промежуточных аргументов u,v,…, где u = f(x ,y,t …), v = g ( x , y , t …) и.т.д.

Если для функции двух переменных z=f(x,y) обе переменные х и у зависят от некоторой третьей переменной t:х=j(t),у=c(t), то z зависит также только от t и можно вычислить производную причем справедлива теорема:

Теорема. Если функции x=x( t ) и  =y( t ) дифференцируемы в точке t , а функция z=f( x , y ) дифференцируема в точке М( x ( t ), y ( t )), то сложная функция z=f ( x ( t ), y ( t )) также дифференцируема в точке t :

Из этой формулы можно вывести и формулы дифференцирования для других форм задания сложных функций.

Для функции двух переменных z =f(x,y ) в случае, когда х=х(u ,v), у=у( u , v ), производные сложной функции z=f(х( u , v ),у( u , v )), по переменным u и v считаются по формулам:

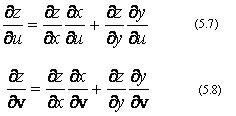
Если z = f(x,y) и у=у(х), то можно вычислять полную производную функции z по переменной х:

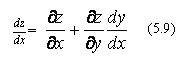
3 4. Полная производная функции — производная функции по времени вдоль траектории. Расчёт полной производной функции по времени t, (в отличие от частной производной, ) не подразумевает, что другие аргументы (т.е. иные нежели аргумент, t, по которому ведётся полное дифференцирование: x и y) постоянны при изменяющемся t. Полная производная включает в себя эти непрямые зависимости от t (т.е. x(t) иy(t)) для описания зависимости f от t. Например, для упомянутой функции f = f(t, x(t), y(t)) полная производная функции вычисляется по следующему правилу:

что упрощается до

Где частные производные.

35.Производная функции, заданной неявно Функция одной переменной – это правило, по которому каждому значению независимой переменной соответствует одно и только одно значение функции .

Неявная функция определяется соотношением. Но не все такие соотношения между x и y задают функцию. Например, ни одна пара действительных чисел x и y не удовлетворяет равенству следовательно, это соотношение неявную функцию не задает. Может неявно определять закон соответствия между величинами x и y, причем каждому значению аргумента x может соответствовать как одно (в этом случае имеем однозначную функцию) так и несколько значений функции (в этом случае функцию называют многозначной).