55. Вычисление длины дуги плоской кривой

Пусть известна функция   и требуется найти длину дуги, заданной функцией   , где   .

Для определения длины дуги   необходимо вычислить определенный интеграл:

Рассмотрим случай параметрического задания кривой:

где   . В этом случае для определения длина дуги   вычисляется определенный интеграл:

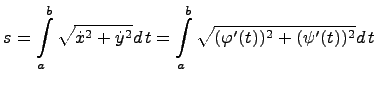
Рассмотрим случай, когда кривая задается в полярных координатах   где  . Тогда для определения длины дуги   вычисляется следующий определенный интеграл:

57. Вычисление объема тела вращения вокруг оси

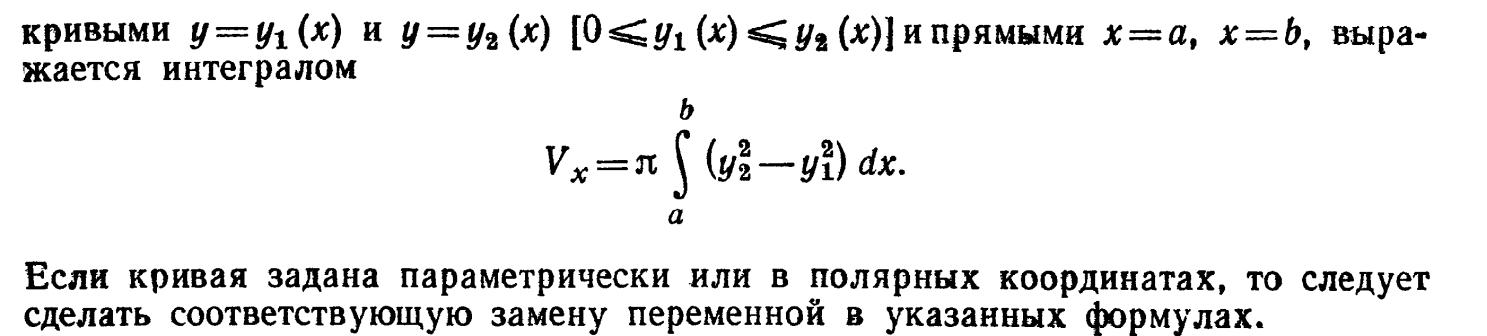
58.Несобственные интегралы с бесконечнми пределами

60. Формулы прямоугольников