
- •81. Разновидности автоматической регистрирующей аппаратуры
- •А) Видеографические регистраторы (безбумажные самописцы)
- •82.Экстраполяция и интерполяция
- •83.Экстраполяция на основе экспериментальных данных
- •84.Разновидности ситуаций, где встречается необходимость
- •85.Численное дифференцирование экспериментальных данных, методы снижения ошибок
- •86. Понятие о технике прогнозирования временных рядов
- •Понятие временных рядов данных. Метод скользящих средних
- •87. Экспериментальные исследования в задачах изучения характеристик телетрафика
- •89. Вопросы достоверности имитационного моделирования
85.Численное дифференцирование экспериментальных данных, методы снижения ошибок
Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции. В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).
Методы численного дифференцирования
применяются, если исходную функцию f(x)
трудно или невозможно продифференцировать
аналитически. Например, эта функция
может быть задана таблично. Задача
численного дифференцирования – выбрать
легко вычисляемую функцию (обычно
полином)
![]() ,
для которой приближенно полагают
,
для которой приближенно полагают
![]() .
.
 Численное
дифференцирование – некорректная
задача, так как отсутствует устойчивость
решения. При численном дифференцировании
приходится вычитать друг из друга
близкие значения функции. Это приводит
к уничтожению первых значащих цифр,
т.е. к потере части достоверных знаков
числа. А так как значения функции обычно
известны с определенной погрешностью,
то все значащие цифры могут быть потеряны.
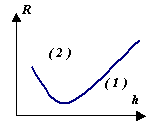
На графике кривая (1) соответствует
уменьшению погрешности дифференцирования
при уменьшении шага; кривая (2) представляет
собой неограниченно возрастающий
(осциллирующий) вклад неустранимой
погрешности исходных данных – значений
функции y(x). Критерий выхода за
оптимальный шаг при его уменьшении –
«разболтка» решения: зависимость
результатов вычислений становится
нерегулярно зависящей от величины шага.
Численное
дифференцирование – некорректная
задача, так как отсутствует устойчивость
решения. При численном дифференцировании
приходится вычитать друг из друга
близкие значения функции. Это приводит
к уничтожению первых значащих цифр,
т.е. к потере части достоверных знаков
числа. А так как значения функции обычно
известны с определенной погрешностью,
то все значащие цифры могут быть потеряны.
На графике кривая (1) соответствует
уменьшению погрешности дифференцирования
при уменьшении шага; кривая (2) представляет
собой неограниченно возрастающий
(осциллирующий) вклад неустранимой
погрешности исходных данных – значений
функции y(x). Критерий выхода за
оптимальный шаг при его уменьшении –
«разболтка» решения: зависимость
результатов вычислений становится
нерегулярно зависящей от величины шага.
86. Понятие о технике прогнозирования временных рядов
Наиболее распространенным способом прогнозирования является прогнозирование на основе временных рядов (динамических рядов, рядов динамики, хронологических рядов). От названия суть не меняется. Временной ряд описывает изменение какого-либо показателя во времени.
Составные элементы временного ряда:
Показатели уровней ряда.
Периоды времени (например, годы или месяцы) или моменты времени (определенные даты).
Временной ряд дает прогнозисту информацию о том, как развивался исследуемый объект в прошлом. На основе этой информации можно сделать вывод о наличие закономерности развития. А коли есть закономерность, то можно предположить, что она сохранится и в будущем. Естественно, на основе полученных данных можно составить прогноз.
Условия применения
Прогнозирование на основе временных рядов как любой метод прогнозирования имеет условия применения.
Данный подход с успехом может применяться лишь в краткосрочном прогнозировании. Собственно говоря, краткосрочный прогноз не имеет строгих рамок. Я бы сказал, что временные ряды можно использовать для прогнозирования на один период вперед. Возможно прогнозирование на более длительный срок, но в этом случае надежность прогноза снижается. Более того, чем дальше период прогноза отстоит от текущего момента, тем больше вероятность того, что существующая тенденция изменится. Тем не менее, даже в долгосрочном прогнозе, использование временных рядов возможно, если оно лежит в основе инерционного сценария развития и применяется на ряду с другими методами.
Для прогноза необходимо также определенное информационное обеспечение, а именно достоверная информация о развитии исследуемого явления минимум за пять периодов (временной ряд).
Структура временного ряда
В общем виде временной ряд можно представить следующим образом:
![]()
![]() -
детерминированная составляющая
временного ряда.
-
детерминированная составляющая
временного ряда.
![]() -
стохастическая (случайная) составляющая
временного ряда.
-
стохастическая (случайная) составляющая
временного ряда.
Детерминированную составляющую можно объяснить, описать с помощью математической модели. Стохастическая составляющая формируется под воздействием большого числа случайных факторов, не отраженных в прогнозной модели. Однако в модели возможно отразить закономерность изменения случайной компоненты.
В детерминированную составляющую могут входить три элемента:
Эволюционная составляющая (характеризует основную тенденцию развития исследуемого объекта).
Циклическая составляющая (формируется под воздействием долговременных циклических факторов).
Сезонная составляющая (показывает колебания показателя в течение года).
Таким образом, прогнозирование на основе временных рядов заключается в создании модели, в которой независимой переменной является время, а зависимой - исследуемый показатель. Следует уточнить, что целью прогнозиста является не построение модели наиболее точно описывающий явление в прошлом, а модель наиболее точно прогнозирующую развитие явления в будущем.
Модели
стационарных и нестационарных временных
рядов. Пусть
![]() Рассмотрим
временной ряд X(t).
Пусть сначала временной ряд принимает
числовые значения. Это могут быть,
например, цены на батон хлеба в соседнем
магазине или курс обмена доллара на
рубли в ближайшем обменном пункте.
Обычно в поведении временного ряда
выявляют две основные тенденции - тренд
и периодические колебания.
Рассмотрим
временной ряд X(t).
Пусть сначала временной ряд принимает
числовые значения. Это могут быть,
например, цены на батон хлеба в соседнем
магазине или курс обмена доллара на
рубли в ближайшем обменном пункте.
Обычно в поведении временного ряда
выявляют две основные тенденции - тренд
и периодические колебания.
При этом под трендом понимают зависимость от времени линейного, квадратичного или иного типа, которую выявляют тем или иным способом сглаживания (например, экспоненциального сглаживания) либо расчетным путем, в частности, с помощью метода наименьших квадратов.
Характеристики
временных рядов.
Для более подробного изучения временных
рядов используются вероятностно-статистические
модели. При этом временной ряд X(t)
рассматривается как случайный процесс
(с дискретным временем). Основными
характеристиками X(t)
являются математическое
ожидание
X(t),
т.е.
![]() ,
,
дисперсия
X(t),
т.е.
![]() и
автокорреляционная
функция
временного
ряда X(t):
и
автокорреляционная
функция
временного
ряда X(t):
![]() т.е.
функция двух переменных, равная
коэффициенту корреляции между двумя
значениями временного ряда X(t)
и X(s).
т.е.
функция двух переменных, равная
коэффициенту корреляции между двумя
значениями временного ряда X(t)
и X(s).
В
теоретических и прикладных исследованиях
рассматривают широкий спектр моделей
временных рядов. Выделим сначала
стационарные
модели. В них совместные функции
распределения
![]() для
любого числа моментов времени k,
а потому и все перечисленные выше
характеристики временного ряда не
меняются со временем.
В
частности, математическое ожидание и
дисперсия являются постоянными
величинами, автокорреляционная функция
зависит только от разности t-s.
Временные
ряды, не являющиеся стационарными,
называются нестационарными.
для
любого числа моментов времени k,
а потому и все перечисленные выше
характеристики временного ряда не
меняются со временем.
В
частности, математическое ожидание и
дисперсия являются постоянными
величинами, автокорреляционная функция
зависит только от разности t-s.
Временные
ряды, не являющиеся стационарными,
называются нестационарными.
ОСТАЛЬНОЕ ИЗ БИЛЕТА, КОТОРЫЙ БЫЛ НА ЭКЗАМЕНЕ. КОМУ ЧТО НРАВИТСЯ.
