УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В ГОРОДЕ СТЕРЛИТАМАК

КАФЕДРА ЕСТЕСТВЕННО-НАУЧНЫХ И ОБЩЕПРОФЕССИОНАЛЬНЫХ ДИСЦИПЛИН

100	2	3	4	5	6	7	8	9	10	11	12
90
80
70
60
50
40
30
20
10

ПРОГРАММИРОВАНИЕ И ИССЛЕДОВАНИЕ АЛГОРИТМОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ

МЕТОД ПРАВЫХ ПРЯМОУГОЛЬНИКОВ.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе по ИНФОРМАТИКЕ

2403.302310.000ПЗ

(обозначение документа)

Группа МАС-102-д	Фамилия, и.о.	Подпись	Дата	Оценка
Студент	Нургалиев И.Р.
Консультант	Карасева Л.М.
Проверил

Стерлитамак 2013 г.

Содержание

Содержание 3

Введение 4

1.Теоретическая часть. 5

1.1 Математическая модель метода. 5

1.2 Блок схема алгоритма метода 6

2. Практическая часть 7

2.1. Создание интерфейса приложения 7

2.2. Кодирование метода 10

2.3. Визуализация 12

2.4. Вычислительный эксперимент 12

2.5 Сравнение результатов выполнения приложения с результатом, полученным в математическом пакете 16

Заключение 17

Введение

Очень часто в различных сферах деятельности приходится встречаться с математическими задачами, для которых не удается найти решение классическими методами или решения выражены громоздкими формулами, которые не приемлемы для практического использования. Поэтому большое значение приобрели численные методы. В большинстве случаев численные методы являются приближенными, так как с их помощью обычно решаются задачи, аппроксимирующие исходные. В ряде случаев численный метод строится на базе бесконечного процесса, который в пределе сводится к искомому решению. Однако реально предельный переход не удается осуществить, и процесс, прерванный на некотором шаге, дает приближенное решение. Кроме того, источниками погрешности являются несоответствие математической модели изучаемому реальному явлению и погрешность исходных данных.

Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения решения, называется итерационным. Итерационные методы дают возможность найти решение уравнения, позволяющего по уже найденным приближениям к решению построить следующее, более точное приближение. Плюсом таких методов является простота реализации на ЭВМ.

Целью курсовой работы по дисциплине «Информатика» является закрепление и углубление студентом теоретических и практических навыков работы на компьютере и умения решать инженерные задачи в изучаемой среде программирования.

Для реализации данной цели необходимо решить следующие задачи:

Вычислить определенный интеграл от функции у = sin²x на промежутке [0; π/2].

Создать в IDE Lazarus приложение, которое будет вычислять значение определенного интеграла на заданном промежутке. Приложение должно содержать не менее трех окон, а также текстовое меню в главном окне, позволяющее выбирать те или иные действия.

Пользователь должен вводить исходный промежуток интегрирования.

Для расчета использовать численный метод правых прямоугольников. Результат вычисления сохранить в текстовый файл.

Представить на графике зависимость значения интеграла от количества разбиений n (n изменяется на интервале [10,200] с шагом 10).

Выполнить решение в математическом пакете и сравнить его с результатами, полученными обоими методами созданного приложения.

1.Теоретическая часть.

1.1 Математическая модель метода.

Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка:

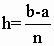
Точки деления будут: x₀=a; x₁=a+h; x₂=a+2× h, ... , x_n-1=a+(n-1)× h; x_n=b. Эти числа будем называть узлами. Вычислим значения функции f(x) в узлах, обозначим их y₀, y₁, y₂, ... , y_n. Cтало быть, y₀=f(a), y₁=f(x1), y₂=f(x2), ... , y_n=f(b). Числа y₀, y₁, y₂, ... , y_n являются ординатами точек графика функции, соответствующих абсциссам x₀, x₁, x₂, ... , x_n. Площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.

Формула правых прямоугольников:

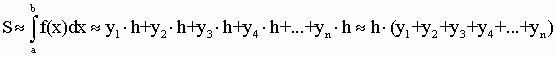
В конечном итоге формула примет вид:

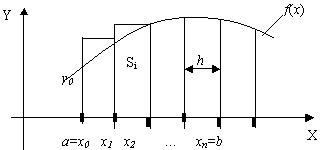
Рисунок 1 - График метода правых прямоугольников