23 Вопрос. Частные виды поверхностей вращения.

Цилиндр вращения, конус вращения. Для цилиндра и конуса вращения меридианами являются прямые линии. Они || оси и равноудалены от нее(для цилиндра) или пересекают ось в одной и той же точке под одним и тем же углом к оси (для конуса).

Цилиндр и конус вращения – поверхности, бесконечные в направлении их образующих , поэтому на изображениях их ограничивают линиями. (меридиан цилиндра- прямоугольник, конуса – треугольник)

• Сфера. Является ограниченной и может быть изображена на чертеже полностью. Экватор и меридианы сферы – разные между собой окружности.

• Тор – Поверхность, при вращении окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр.

В построениях на чертежах широко используют две системы: В плоскостях, перпенд–ых его оси и В плоскостях, проходящих через ось тора.

24 Вопрос. Изображение многогранников.

Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и стороны многогранников являются вершинами и ребрами многогранников. Они образуют пространственную сетку. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранник называют выпуклым, все его грани – выпуклые.

Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные n-граней - параллелограммы, называется n-угольной призмой. Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы

Многогранник, у которого одна из граней – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину, называются пирамидой.

Если пирамиду отсечь плоскостью параллельной основанию, то получим усеченную пирамиду.

25 вопрос. Пересечение поверхности плоскостью.

Для построения применяют вспомогательные плоскости. Точки искомой линии определяются в пересечении линий, по которым вспомогательные секущие плоскости пересекают данные поверхность и плоскость.

При подборе вспомогательных плоскостей надо стремиться к упрощению построений.

Если секущая плоскость – плоскость частного положения, то задача упрощается, та как одна проекция линии пересечения плоскости с кривой поверхностью уже имеется и совпадает со следом секущей плоскости.

26 вопрос. Конические сечения.

Конические сечения образуются при пересечении прямого кругового конуса с плоскостью. К коническим сечениям относятся кривые второго порядка: эллипс, парабола и гипербола, а также пара параллельных прямых.

Эллипс образуется, когда секущая плоскость пересекает все образующие конуса в точках одной его полости; парабола – когда секущая плоскость параллельна одной из касательных плоскостей конуса; гипербола – когда секущая плоскость пересекает обе полости конуса.

Пересечение плоскости с конической поверхностью в зависимости от угла наклона образует:

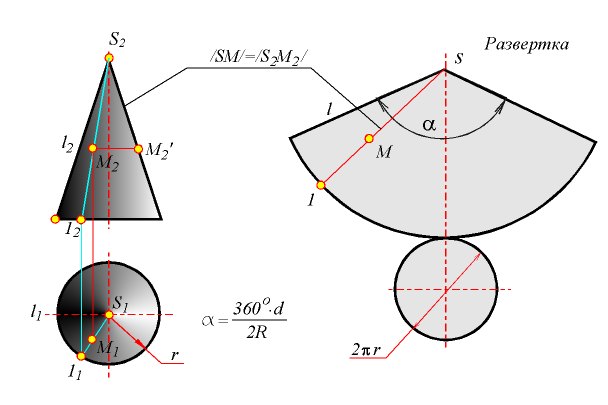
28 вопрос. Развертки поверхностей. Построение развертки конуса.

Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с поверхностью всех его граней.

Построение развертки боковой поверхности пирамиды можно проводить в следующем порядке.

1. Определить длину ребер и сторон основания пирамиды;

2. Выполнить чертеж развертки последовательным построением треугольников – граней пирамиды.

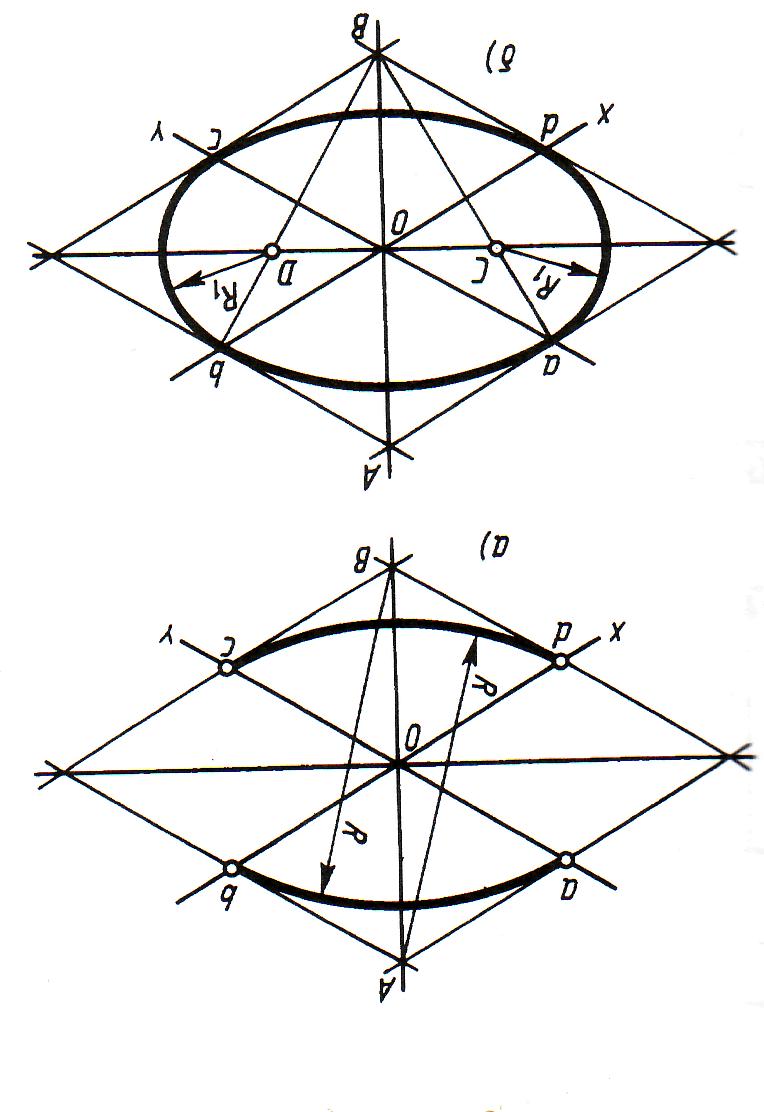
29 вопрос. Аксонометрия. Построение окружности в изометрии и диметрии.

Используют для наглядного изображения.

При || проецировании, если направление проецирования перпендикулярно аксонометрической плоскости проекций, аксонометрическую проекцию называют прямоугольной. Если направление проецирования не перпендикулярно, то называют косоугольной.

Окружность: Окружности в изометрии изображаются в виде эллипсов. Для упрощения работы эллипсы заменяют овалами, вписанными в ромб со стороной, равной диаметру заданной окружности. Для этого на осях (например x и y) откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности. Через полученные точки a, b, c, d проводят прямые, образующие ромб. Из точек А и В проводят дуги радиусом R между точками a и b, c и d. Точки C и D являются центрами малых дуг, сопрягающих большие. Малые дуги описывают радиусом R1. Аналогично строят овалы на осях z и x, z и y.

Окружности в диметрии: Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы

расположение осей