Разрешающая способность и функция неопределённости пачки радиоимпульсов.
ТИ
1…10 мс
……….
И
1…0.1мкс
t
ТПАЧКИ
1/ ТИ
спектр
сигнала
1/ТП
t
2/И
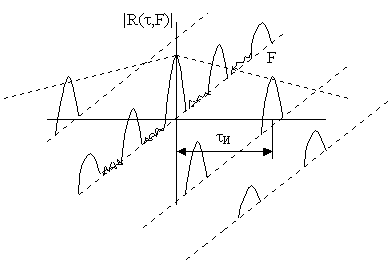
Для обеспечения однозначного измерения дальности период следования импульсов ТИ должен быть как можно большим. Для однозначного измерения скорости необходимо ТИ выбирать как можно меньше. В связи, с тем, что корреляционная функция и в частотной и во временной области имеет гребенчатую структуру, то и функция неопределённости представляет собой комбинацию из многих вершин.
F
1/TП
И
Применение внутриимпульсной модуляции для создания сложных сигналов.
F 1/И B = F*И = 1 для простого сигнала
У сложного сигнала ширина спектра F >> 1/И B = F*И >> 1
Импульсы с линейной частотной модуляцией (ЛЧМ) :
П
ример
сложного сигнала
G(f)
f2
f
Fm
f
1
t f
Fm
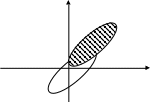
График сечений диаграммы неопределённости для ЛЧМ сигнала.
Анализ данной диаграммы неопределённости показывает, что она представляет собой эллипс, главная ось которого ориентирована под наклоном к системе координат (,F).
Е
сли
бы импульс не содержал частотной
модуляции, то эллипс был бы ориентирован
вдоль оси
и разрешающая способность по времени
определилась бы длительностью импульса
ТИ.
За счёт введения ЧМ появляется наклон
эллипса, который тем больше, чем полоса
ЧМ Fm.
Достоинством данного вида сигнала
является то, что разрешающая способность
по времени определяется как 1/Fm,
а по частоте : 1/И
, т.е. совершенно разными физическими
параметрами сигналов.
S(t) |R(,F)|
1 F
t
R()1
t
-И И
R(,F1)
И
t
R(,F2) 
F
Fm
t
R(,F3)
1/И
t
1/Fm
F1 < F2 < F3
К сожалению, в исключительных случаях, когда присутствует одновременно смещение и по времени и по частоте вдоль оси наклонного эллипса ЛЧМ сигнал обладает плохой разрешающей способностью. Но при больших длительностях импульса и Fm, эллипс вырождается в тонкую вытянутую линию и вероятность такого сообщения становится малой.
Схемотехнические методы построения импульсов с линейной частотой модуляции.
f1f2f3f4
…..fВ
t
f
fВ
fН
t
Согласованный фильтр должен строиться на многоотводных линиях задержки. Это будет система узкополосных фильтров, каждый из которых будет настроен на свою частоту, а затем результат должен поступить на линию задержки и на выходе получим сжатый сигнал.
Ф1
f1f2f3f4
…..fВ
t
AD
Ф1
Ф2 AD t
Ф2
ЛЗ t
AD Ф3
Ф3
t
. ФВ
AD
t
ФВ
ОТКЛИКА >= 1/Fm
U
t
Амплитуда откликов возрастает в n – раз, а длительность отклика укорачивается т.е. происходит сжатие импульсного сигнала во времени.
Существует 2 – й вид ЛЗ.
ЛЗ fВХ
Ф1 Ф2 Ф3 …… ФВ
Ф1
UВХ Ф2
Ф3
ФВ
UВЫХ
t
Данное строение схемы не учитывают - структуры сигнала и не позволяет осуществить шифрование сложных ВЧ – составляющих на выходе отводов линий задержки более. На практике для формирования ЛЧМ сигнала и его последующего сжатия используется фильтры на поверхностно – акустических волнах (ПАВ). Эти фильтры срезают собой кристаллическую структуру на поверхности которой нанесены металлические электроды. Структура электродов нанесена с линейно – изменяющимся интервалом или периодом.
Поверхностно – акустическая волна – это сигнал передвинутый на десятки и сотни кГц и можно сформировать звуковую волну. Если на вх1 подать - образный импульс, то на вых1 мы получим сначала положительный всплеск, потом отрицательный, и так чередуются, но частота этих спектров будет изменяться по линейному закону.
Вх1
t
Вых1
t
После сжатия
t
Такой фильтр используют в радиолокации.
Поскольку данный фильтр формирует ЛЧМ сигнал при возбуждении ВХ1 - образным воздействием, то такой фильтр является оптимальным, согласованным для сформированного сигнала. Фильтры на ПАФ позволяют обеспечить коэффициент сжатия до 10 4 , что позволяет обеспечить большинство требований по совместному разрешению как по времени, так и по частоте. Недостатком ЛЧМ сигналом является наличие зоны неопределённости, когда неодновременное смещение сигнала и его времени и по частоте совпадает с осью диаграммы неопределённости.
F
Наиболее привлекательными является сложенные сигналы диаграммы неопределённости которых имеет площадь меньше единицы, а функция неопределённости имеет форму кнопки.
|R(,F)|
1
0.5 F
Корреляционная функция спектрального шума (имеет одинаковою плотность вероятности), то достаточно сравнить 2 процесса без временного сдвига.
t
R()
1
0.5
0
Поскольку на практике для формирования таких сигналов используются генераторы псевдослучайных последовательностей, последовательность детерминирована, но обладает корреляционными свойствами шумовой последовательности .
Примером такой последовательности в простейшем случаи является коды Баркера.
Фазоманипулированные сигналы на основе псевдослучайных последовательностей.
Обозначается ФМн – это согнутая последовательность и решённых радиоимпульсов в единичной длительности и частоты, но фаза каждого импульса имеет своё определённое значение.
= 0 =0 =180 =180
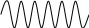
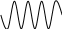
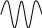
1
ФМн – называется, рассматриваемая 2 – х позиционная в практике систем радиосвязи широко используется 2 – х позиционные и 4 – х позиционные и в некоторых случаях до 32 позиций.
0,180
0,90,180,270
Увеличение количества отчетов > 4 приводит к ухудшению.