Совместная разрешающая способность во временно – частотной области.

Принцип неопределённости :

Повышение разрешающей способности во времени требует укорочения импульса, а повышение разрешающей способности по частоте, требует сужения спектра, следовательно обеспечение одновременного улучшения разрешающей способности по времени и по частоте для происходящих сигналов невозможно. И мы должны одновременно анализировать это и обе разрешающие способности. Это делается с помощью двумерной нормированной автокорреляционной функции сигнала во время – частотной области, эта функция называется функция неопределённости.

Функция неопределённости записывается следующим образом :

В другом учебнике :

Построим два графика :

Сечение функции неопределённости во временной области при наличии частотной расстройки. И 2 – й в частотной области, при наличии временной расстройки.

_И

S(t) G(t)

t v f

S(t-) смешение смещение

t G(f-F)

R(,0) 1 f

0.5 |R(0,F)|

0.5

t

1/_И 1/_И f

R(,F₁) 1 |R(₁,F)|

0.5

F₂ >F₁

_И _И t 1/_И- 1/_И- f

R(_,F₂) 1 |R(₂,F)| 0.5

t

f

Функция неопределённости прямоугольного импульса.

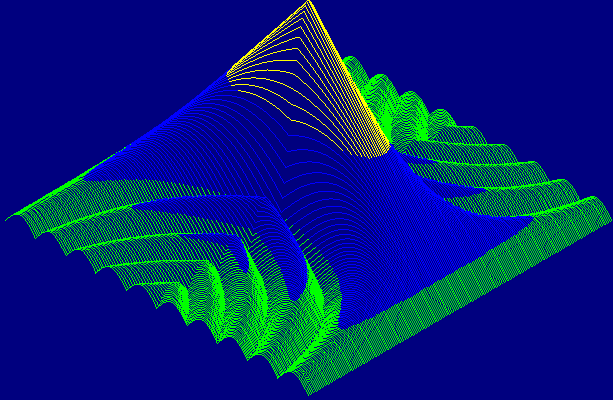
Свойства функции неопределённости.

1) Полученная фигура обладает центральной симметрией, вокруг оси |R(F,)|.

2) Вершина фигуры, находится в точке |R(0,0)| = 1

3) Объём ограниченный функцией неопределённости и называемой телом неопределённости, всегда постоянен и равен единице.

Сечение тела неопределённости на уровне 0.5 называется диаграммой неопределённости.

F

_И

1/_И



|R(F,)| = 0.5 |R(F,)| = 0.01

2T_И

Свойства диаграммы неопределённости :

Её площадь постоянна и равна еденице для простых сигналов.

Сжатие этой диаграммы по времени  приводит к вытягиванию по оси частот, то есть

Укорочение импульса по времени приводит пропорционально расширению его спектра или улучшению разрешающей способности по времени приводит к ухудшению разрешающей способности по частоте и наоборот, для простых сигналов.

Функция неопределённости Гауссова одиночного импульса.

|R(,F)|

F

0.5

Z

t

U(t)

1

0.5

_И0.5 t

|G(f)|

f

Корреляционная функция Гауса импульса и в частотной области описывается Гаусовской огибающей колоколо – образной формы. Сечение на уровне 0.5 представляет собой правильный эллипс. Площадь остаётся постоянной т.к площадь диаграммы неопределённости const и близка к единице укорочение длительности импульса приводит к деформации эллипса, при этом разрешающая способность по времени  улучшается, а по частоте – пропорционально ухудшается. Использование простых сигналов и одиночных немодулированных импульсов не позволяет обеспечить высокую разрешающую способность и по времени и по частоте.

Пример : РЛС имеет :

_И = 1мкс – длительность импульса

 = 3см – длина волны

с = 3*10⁸ м/с – скорость света

Определим разрешающую способность по дальности :

(D) = с*_И/2 = 150 м.

по скорости :

(V) = *(1/_И)/2 = 15 км/с

усложним зондирующий сигнал : увеличение длительности сигнала.