49. Дайте определение передаточной функции.
П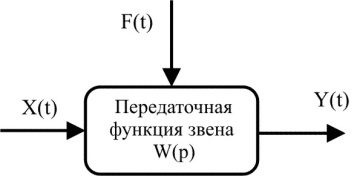
ередаточная
функция определяется как отношение
между изображениями Лапласа выходного
и входного сигналов Для схемы (1)
передаточная функция может выглядеть
следующим образом:
схема 1
50. Обычно тип звена определяется соотношением между сигналами на его выходе и входе. Какими могут быть эти соотношения?
В зависимости от типа звена соотношение между выходным и входным сигналами звена может выражаться в виде:
Математических функций, например: синуса, косинуса, логарифма, показательной функции и т. п. Число, поданное на вход такого блока, подставляется в реализуемую блоком функцию в качестве аргумента.
Математических операций (сложение и вычитание, взятие производной либо интегрирование).
Т. н. коэффициента передачи, т.е. простого отношения выход/вход.
51. На чём основан физический подход к моделированию механических систем?
Физический подход к моделированию динамических систем основан на уравнениях баланса сил, массы, энергии и моментов.
При физическом подходе к моделированию динамических систем переменными модели являются физические состояния процессов в реальной системе, такие как: силы, ускорения, скорости, углы, температуры, напряжения и т.п. Изменение состояний производится процедурами, реализующими соответствующие законы динамики с учетом существующих ограничений и отношений между элементами системы. В процессе физического моделирования задаются некоторые характеристики внешней среды, и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды.
Механические системы
К
раеугольным
камнем динамической модели любой
механической системы является второй
закон Ньютона. Для применения закона
Ньютона необходимо задать некоторую
систему отсчета относительно которой
будут определяться положение, скорость
и ускорение. Пусть вектор F
– сумма всех сил, действующих на тело,
m
– масса тела, а вектор z
характеризует его положение. Ускорение
a
– вектор с тем же направлением, что и
вектор F.
Уравнение баланса сил имеет вид: Второй
закон Ньютона можно записать как систему
дифференциальных уравнений первого
порядка, в форме так называемых уравнений
состояния. При прямолинейном движении
координата z
и скорость υ
выражаются как скаляры:
(4.7)
Закон Ньютона для систем вращения имеет вид:
(4.8)
где Т – сумма всех моментов, действующих на тело, J – момент инерции и ω – угловая скорость (рисунок 4.2). Часто J – непостоянная величина, например, при работе промышленного робота или прокатного стана, и нужно учитывать его зависимость от времени.
Рисунок 4.2 – Закон Ньютона для вращения
Если ввести понятие угла поворота ε, то динамику вращения можно описать в форме уравнений состояния. При этом полагают, что известно направление вращения и что величина J постоянна. Тогда дифференциальные уравнения записываются в виде:
(4.9)
Уравнения Лагранжа являются обобщенной формой кона Ньютона. Существуют деформируемые механические системы, например, крыло самолета при Движении которых могут появляться нежелательные колебания такие динамические системы, вообще говоря, очень сложны для управления.