2.2. Произведение классов Фиттинга.

Определение 55. Пусть и произвольные классы групп. Гашюцевым произведением классов и называется класс всех групп, являющихся расширением некоторой группы с помощью группы.

Обозначается: или .

Определение 56. Пусть класс групп, формация. Корадикальным (формационным) произведением классов групп и называется класс групп

Определение 57. Пусть класс Фиттинга и класс групп. Радикальным произведением и называется класс .

Теорема 10. Если и классы Фиттинга, то класс Фиттинга и .

Доказательство.

Покажем, что класс Фиттинга.

1. Пусть и . Покажем, что . Поскольку , то . Из по лемме 9 получаем:

. Так как , то по теореме о соответствии получаем:

. По условию , класс Фиттинга, значит, . Тогда . Следовательно, .

2. Пусть . Покажем, что . Из следует: . Так как , то . Значит, . Аналогичным образом получается, что и .

Рассмотрим . Следовательно, .

Из 1) и 2) получаем, что класс Фиттинга.

Покажем, что .

Пусть . Покажем, что . Так как , то . Следовательно, . Значит, и .

Теорема 11. Пусть 𝔛, 𝔉 и классы Фиттинга. Тогда

1. ;

2. .

Доказательство.

1. По теореме 10 класс Фиттинга, . Значит,

. Так как , то . Следовательно, по теореме о соответствии получим: и

.

Покажем обратное включение. Пусть . Так как , то . Но в силу того, что , , а значит, . Из обоих включений получаем, что .

Так как , то . Следовательно, . Поэтому . Тогда по теореме о соответствии , откуда следует, что .

Таким образом, .

2. Пусть . Тогда . Значит,

.

Следовательно, и .

Тогда . Покажем обратное включение.

Пусть . Тогда 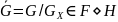. Так как

и по первому пункту теоремы получаем: Значит, .

Теорема 12. Если класс Фиттинга и гомоморф, то

.

Доказательство.

Из определения радикального произведения следует, что

, то есть радикальное произведение состоит из таких групп , что и . Следовательно, . Покажем обратное. Пусть . Рассмотрим факторгруппу . Так как гомоморф, то . Откуда следует, что .

Глава 3. Произведение -веерных классов Фиттинга.

3.1 -веерные классы Фиттинга и их основные свойства.

_{Определение 54}. Функцию {классы Фиттинга групп} называют _{- радикальной функцией простого натурального аргумента или, коротко, -функцией. Функцию {классы Фиттинга групп} называют радикальной функцией простого натурального аргумента или, коротко, -функцией.}

_{Лемма 10. Пусть – – функция, - -функция и и для всех }. Тогда является классом Фиттинга.}

_{Определение 55. Класс Фиттинга называют -веерным, если , где и - некоторые -функция и -функция соответственно. Функцию называют -спутником, а функцию -направлением -веерного класса Фиттинга . Пусть - -функция. Класс Фиттинга называется веерным, а называется -спутником веерного класса Фиттинга .}

Лемма 11. Пусть группа минимального порядка из , где и классы Фиттинга. Следовательно, комонолитична с комонолитом .

_{Лемма 12}. Пусть -класс Фиттинга и . Тогда , где - _{-функция такая, что , для всех и -произвольная -функция. В частности, классы Фиттинга и (1) являются -веерными для любого непустого множества .}

_{Доказательство.}

_{Пусть , где и – из условия леммы. Покажем, что . Пусть . Тогда и из следует, что . Таким образом, и, значит, .}

_{Предположим, что и -группа наименьшего порядка из . Тогда является комонолитической группой с комонолитом . Поскольку , то и . Пусть . Тогда и , что невозможно. Следовательно . Лемма доказана.}

_{Лемма 13. Пусть , где -произвольная -функция. Тогда справедливы следующие утверждения:}

1. _{, где для любого ;}

2. _{, где и для всех ;}

3. _{если и , то и для всех .}

_{Доказательство:}

1. _{Пусть , где - -функция из условия леммы. Покажем, что . Так как для любого , то . Пусть . Тогда по определению классов Фиттинга, и для любого . Так как , то и для любого , следовательно и для любого . По определению -веерного класса Фиттинга заключаем, что . Таким образом, . Тем самым мы показали, что .}

2. _{Пусть , где - из условия леммы. Покажем, что . Пусть . Тогда и для любого и, кроме того, . Таким образом и для любого . Следовательно, по определению -веерного класса Фиттинга, имеем . Значит . Допустим, что . Пусть , -группа минимального порядка с таким свойством. Тогда, по лемме Ц, комонолитична с комонолитом . Допустим, что . Тогда, так как , то . Противоречие. Значит, и . Поэтому и из . Следовательно, . Поэтому . Так как , то есть и , то . Далее, из следует, что для любого . Таким образом, по определению -веерного класса Фиттинга, заключаем, что . Противоречие. Следовательно, допущение не верно и .}

3. _{Пусть и . Так как (по условию), то существует . Поэтому и, значит, . Из (так как ). А получаем, что следовательно для любого .}

_{Определение 56. Направление -веерного класса Фиттинга назовают:}

_{-направлением, если для любого ;}

_{-направлением, если для любого ;}

_{-направлением, если для любого ;}

_{-направлением, если формация Фиттинга -разрешима для любого .}

_{Пусть – множество направлений -веерного класса Фиттинга . -функцию называют -направлением -веерного класса Фиттинга , если является -направлением для любого . Направление -расслоенного класса Фиттинга называется -направлением , если для любой неабелевой группы .}

_{Лемма 14. Пусть с -направлением и . Тогда}

1. _{Если , и , то .}

2. _{Если и , то .}

3. _{Если , для любого и , то .}

_{Доказательство:}

1. _{Так как и , то . По условию . Пусть . Тогда . Поскольку является -направлением, то и по лемме 1, п.9 получим и, значит, по определению , имеем .}

2. _{По условию и . Пусть . Так как является - группой и является – направлением, то по лемме 1, п.9 имеем для всех . По определению имеем .}

3. _{По условию и для любого . Пусть . Тогда является - группой. Так как является -направлением, то по лемме 1, п.9 получим . Следовательно. для всех и, значит, по определению , имеем . Лемма доказана.}