2. Элементы теории классов групп.

Определение 49. Классом групп называется всякое множество групп, которое вместе с каждой своей группой содержит и все группы, изоморфные ей.

Если группа (подгруппа) принадлежит классу групп , то называют - группой (подгруппой).

Определение 50. Операцией на классах групп называется отображение множества классов групп в себя.

Произведение операций определяется следующим образом:

. И вообще: .

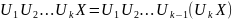Рассмотрим следующие операции на классах групп:

когда является подгруппой некоторой группы, то есть отображение, которое ставит в соответствие классу групп класс групп, состоящий из всех подгрупп всех групп;

когда является нормальной подгруппой группы;

когда является гомоморфным образом некоторой группы;

когда является произведением конечного числа своих нормальных подгрупп;

когда является прямым произведением своих нормальных подгрупп;

Определение 51. Класс групп называется замкнутым относительно операции или замкнутым, если .

Определение 52. Класс групп называется:

1. замкнутым или наследственным, если , то есть всегда ;

2. замкнутым или нормально наследственным, если , то есть всегда ;

3. замкнутым или гомоморфом, если , то есть всегда ;

4. замкнутым, если , то есть если , то ;

5. замкнутым, если , то есть если

то .

Лемма 5. Для произвольного класса групп справедливо:

1. , то есть ;

2. , то есть ;

3. , то есть ;

4. ;

5. .

Теорема 9. Если класс замкнут относительно произведений нормальных подгрупп, то каждая субнормальная подгруппа группы содержится в некоторой нормальной подгруппе группы .

Следствие 1. Пусть класс замкнут относительно произведений нормальных подгрупп. Если и субнормальные подгруппы группы , то субнормальная .

Глава 2. Классы Фиттинга конечных групп.

2.1. Классы Фиттинга и их основные свойства.

Определение 53. Класс групп называется классом Фиттинга, если выполняются следующие условия:

1. из всегда следует, что (1)

2. из всегда следует, что

. (2)

Пример. Класс нильпотентных групп является классом Фиттинга.

1. Действительно, из по лемме 4 1) следует, что .

2. По лемме 4 2) из в силу выполнимости условий определения внутреннего произведения подгрупп группы следует, что .

Лемма 6. Пусть непустой класс Фиттинга. Тогда для любой группы :

1. ;

2. тогда и только тогда, когда ;

3. наибольшая нормальная подгруппа группы .

Лемма 7. Пересечение любой совокупности классов Фиттинга является классом Фиттинга.

Доказательство.

Пусть классы Фиттинга, . Покажем, что класс Фиттинга.

1. Пусть . Покажем, что . Поскольку , а , то по определению операции пересечения получаем: . Тогда из определения класса Фиттинга следует, что . Поэтому .

2. Пусть . Покажем, что . Так как , то . Поскольку классы Фиттинга, то

. А это означает, что

.

Определение 54. Пусть непустой класс Фиттинга. радикалом группы называется произведение всех ее нормальных подгрупп.

Лемма 8. Пусть класс Фиттинга, группа и . Тогда и только тогда , когда .

Доказательство.

Пусть и . По следствию 1 получаем, что и

.

Обратно, пусть и . Так как и выполняется требование (1), то .

Лемма 9. Если класс Фиттинга и , то .

Доказательство.

Так как и , то . Поскольку , то . Обратно, , поэтому и по лемме 8 подгруппа . Итак, .