Глава 1. Определения, обозначения и известные результаты, используемые в работе.

1. Элементы теории групп.

Определение 1. Под множеством понимают совокупность объектов, рассматриваемых как единое целое.

Определение 2. Множество, содержащее хотя бы один элемент, называется непустым.

Определение 3. Множество М называется конечным, если оно содержит конечное число элементов.

Определение 4. Пересечением множеств А и В называется множество, состоящие из всех элементов принадлежащих и множеству А и множеству В одновременно. Обозначается АВ, т.е. АВ={x | xА и xВ}.

Определение 5. Бинарное отношение f между множествами A и B называется функциональным отношением, если из (a,b) f и (a,c) f следует, что b=c .

Определение 6. Функциональное отношение f между множествами A и B называется функцией или отображением A в B, если Dom f=A, и обозначается f : A B или A B.

Замечание. Если f: A B – функция, то каждому элементу a A соответствует единственный элемент b B и записывается f(a)=b (a,b) f afb.

Определение 7. Пусть – отображение. Отображение называется сюрьективным, если , то есть .

Определение 8. Отображение f : A B называется инъективным, если из всегда следует, что .

Определение 9. Отображение f : A B называется биективным, если оно сюрьективно и инъективно.

Определение 10. Пусть f : A B – отображение. Если , то f называется гомоморфным отображением множества в .

Если подмножество группы A, то образ при гомоморфизме , а образ гомоморфизма , который обозначают через .

Ядром гомоморфизма называется множество , где единичный элемент группы B.

Через обозначают множество всех гомоморфизмов группы на группу .

Определение 11. Гомоморфное отображение f множества в называется изоморфизмом, если f – биекция.

Теорема 1 (основная о гомоморфизмах).

Пусть . Тогда .

Теорема 2. Пусть . Тогда .

Теорема 3. Пусть , . Тогда .

Теорема 4 (об естественном гомоморфизме).

Пусть группа, . Тогда существует гомоморфизм такой, что , который называется естественным гомоморфизмом.

Определение 12. Бинарной алгебраической операцией на множестве М называется отображение .

Определение 13. Бинарной алгебраической операцией на непустом множестве М называется закон или правило, по которому любым двум элементам множества М, не обязательно различным, взятым в определенном порядке, ставится в соответствие единственный элемент множества М. Обозначается: φ(a, b)=c.

Замечание. Если на множестве М задана бинарная алгебраическая операция «∗», то для любых существует единственный элемент . В этом случае говорят, что множество М замкнуто относительно операции «∗».

Говорят, что на множестве определена бинарная алгебраическая операция (умножение), если для всех .

Определение 14. Пусть «∗» – бинарная алгебраическая операция на непустом множестве М. Элемент называется правым (левым) симметричным элементом для элемента относительно операции «∗», если ∗ ( ∗ ), где - правый (левый) нейтральный элемент множества М относительно операции «∗».

Определение 15. Если правый симметричный элемент для элемента относительно операции «∗» является и левым симметричным элементом, то называется симметричным для элементом, причем ∗ ∗ .

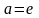Определение 16. Пусть «∗» – бинарная алгебраическая операция на непустом множестве М. Элемент называется правым (левым) нейтральным элементом относительно операции «∗», если ∗ ( ∗ ) для любого .

Определение 17. Если элемент является правым и левым нейтральным элементом относительно операции «∗», то он называется нейтральным элементом в М относительно операции «∗», причем для любого ∗ ∗ .

Замечание. Правый (левый) нейтральный элемент относительно операции «⋅» называется правым (левым) единичным элементом, а правый (левый) симметричный элемент для элемента а - правым (левым) обратным к а и обозначается а^-1.

Определение 18. Пусть «∗» – бинарная алгебраическая операция на непустом множестве М. Операция «∗» называется

• коммутативной на множестве М, если a,b М: a∗b = b∗a.

• ассоциативной на множестве М, если a, b, c М:

(a∗b)∗c =a∗(b∗c).

Определение 19. Непустое множество , замкнутое относительно бинарной алгебраической операции «∗» называется группой, если выполняются следующие аксиомы (аксиомы группы):

1. операция «∗» ассоциативна на ,т. е. а∗(b∗c) = (a∗b)∗c для любых  a, b, c∈ .

2. в существует нейтральный элемент относительно операции «∗», т. е. ∃e∈ : a∗e=e∗a=a, для любого a∈ .

3. в для любого элемента существует симметричный ему элемент, т. е. для любого a∈ ∃a'∈ : a∗a'=a'∗a=e.

Определение 20. Группа относительно операции «∗» называется абелевой, если операция «∗» коммутативна на , то есть a∗b=b∗a для любых a, b∈ .

Определение 21. Группа относительно операции умножения называется мультипликативной.

Определение 22. Если – конечное множество, являющееся группой, то называется конечной группой, а число элементов в – порядком группы .

Определение 23. Непустое подмножество группы называется подгруппой группы ,если является группой относительно тех же операций, что и .

Обозначение: .

Теорема 5 (критерий подгруппы). Пусть группа, . Следовательно, тогда и только тогда, когда

1. ;

2. .

Лемма 1. Пусть группа.

1. если , то .

2. если , то .

Определение 24. Пусть группа, , . Правым (левым) смежным классом группы по подгруппе с представителем называется множество .

Определение 25. Пусть группа, , все правые смежные классы группы по подгруппе . Равенство называется разложением группы по подгруппе .

Определение 26. Число смежных классов в разложении группы по подгруппе называется индексом подгруппы в группе и обозначается .

Теорема 6 (Лагранжа). Если подгруппа конечной группы , то

.

В частности, порядок конечной группы делится на порядок каждой своей подгруппы.

Лемма 2. Пусть группа, , . Множество является мультипликативной группой относительно операции, заданной по правилу: , которая называется факторгруппой группы по подгруппе .

Определение 27. Группа называется гомоморфным образом группы , если , где .

Определение 28. Подгруппа группы называется нормальной в группе и обозначается , если .

Определение 29. Группа называется простой, если она не имеет нетривиальных нормальных подгрупп.

Определение 30. Пусть группа, ее подгруппы. Произведение определяется как множество элементов , где . Если , то говорят, что группа является произведением своих подгрупп .

Теорема 7. Пусть группа, ее подгруппы. тогда и только тогда, когда .

Теорема 8. Пусть группа, . Тогда

1. если , то ;

2. если , то .

Определение 31. Группа называется внутренним прямым произведением своих подгрупп , если:

1. ;

2. ;

3. .

Определение 32. Наименьшее натуральное число , при котором

, называют порядком элемента и обозначают .

Определение 33. Элемент называется элементом, если , .

Определение 34. Группа называется группой, если всякий ее элемент является - элементом.

Определение 35. Силовской подгруппой конечной группы называют такую подгруппу, индекс которой не делится на .

Определение 36. Группа называется нильпотентной, если все ее силовские подгруппы нормальны.

Лемма 3. Нильпотентная группа является прямым произведением своих силовских подгрупп.

Лемма 4. 1) Подгруппа и факторгруппа нильпотентной группы нильпотентны.

2) Прямое произведение нильпотентных групп является нильпотентной группой.

Определение 37. Пусть группа. Цепью подгрупп называется последовательность подгрупп , соединяющих подгруппы и .

Определение 38. Пусть группа. Цепь подгрупп вида называется рядом группы .

Определение 39. Ряд группы называется 1) субнормальным, если ;

3. нормальным, если .

Определение 40. Пусть - субнормальный ряд конечной группы ( ). Факторгруппа называется фактором группы .

Определение 41. Субнормальный ряд группы , не допускающий уплотнения без повторения членов ряда, называется композиционным рядом.

Определение 42. Нормальный ряд группы , не допускающий уплотнения без повторения членов ряда, называется главным рядом.

Определение 43. Факторы композиционного ряда называются композиционными факторами.

Факторы главного ряда называются главными факторами.

Определение 44. Подгруппа называется субнормальной подгруппой группы , если существуют подгруппы такие, что .

Запись означает, что субнормальная подгруппа группы .

Определение 45. Группа называется расширением группы с помощью группы, если .

Определение 46. Пусть подмножество группы . Пересечение всех подгрупп группы , содержащих подмножество , называется подгруппой, порожденной подмножеством , и обозначается .

Теорема 9 (о соответствии). Пусть группа, . Тогда

1. если и , то ;

2. каждая подгруппа факторгруппы имеет вид , где подгруппа группы и ;

3. отображение является биекцией множества на множество , где совокупность всех подгрупп группы , содержащих подгруппу ; совокупность всех подгрупп группы ;

4. если , то нормальная подгруппа группы тогда и только тогда, когда нормальная подгруппа факторгруппы .

Определение 47. Группа называется комонолитической, если она содержит единственную максимальную нормальную подгруппу (комонолит).

Определение 48. Нормальная подгруппа группы называется максимальной нормальной подгруппой группы , если следует, что или .