Числовые ряды

Числовые знакоположительные ряды

Пусть задана числовая последовательность, которая называется числовым рядом

(1)

Числа U_i – члены ряда

U_n обозначает общий член ряда

Сумма конечного числа первых членов ряда, называется частичной суммой ряда

(1.1)

Числовой ряд (1) называется сходящимся, если существует конечный предел

(1.2)

Если предел (1.2) не существует, то ряд расходится.

Пример:

Рассмотрим ряд , который является геометрической прогрессией, со знаменателем = q

Cуществует формула для частичной суммы конечного числа членов этого ряда:

а) Если │q│< 1, тогда

существует конечный предел, ряд сходится

б) Если │q│> 1, тогда

конечный предел не существует, ряд расходится

в) Если q = 1, тогда

г) Если q = - 1, тогда

значит,

Определение:

Из (1.3) для сходящегося ряда следует

Чем больше возьмём членов, тем точнее вычислим сумму сходящегося ряда.

Свойства:

1)На сходимость ряда не влияет отбрасывание конечного числа его членов.

(1.4)

2)Если ряд (1) сходится, то сходится и ряд

Возьмём частичную сумму ряда (1.4)

К = const ≠ 0

Из этого следует что ряд (1.4) сходится и его сумма равна K∙S

3) Пусть даны два сходящихся ряда:

Тогда ряды

и их суммы равны S + S* S - S*

соответственно

Следовательно, сходящиеся ряды можно последовательно складывать и вычитать.

4) Пусть дан сходящийся ряд (1)

не нарушая порядка слагаемых объединим их в некоторые группы. Получим другой ряд (2.3) тогда ряд (2.3) сходится и имеет туже сумму S, что и ряд (1)

Признаки сходимости знакоположительных числовых рядов.

1) Необходимый признак сходимости (но недостаточный)

Теорема: Если ряд (1) сходится, то

Доказательство:

Вывод: 1) Если известно, что ряд сходится, то

2) Если , то определить сходится ряд или расходится этим методом невозможно.

3)Если

Пример:

Пример:

 ряд

расходится

Достаточные признаки.

1 )Признак Даламбера.

Пусть дан ряд (1), если существует

Пример:

2) Радикальный признак Коши.

Пример:

Исследовать сходимость ряда

3) Интегральный признак Коши.

Теорема: Рассмотрим ряд с положительными не возрастающими членами, где U_n=f (n)

Тогда ряд сходится или расходится в зависимости от того сходится или расходится несобственный интеграл , где f(x)- непрерывная, невозрастающая функция.

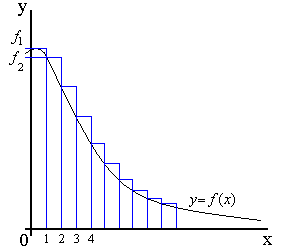
Геометрически ряд – сумма площадей ступенек.

Пример:

Рассмотрим гармонический ряд

Применим признак Даламбера.

Применим интегральный признак Коши.

Признаки сравнения.

Пусть даны два ряда с положительными членами

тогда, если для любого n

а) и ряд (1) сходится, то сходится и ряд (2).

б) если и ряд (1) расходится, то расходится и ряд (2) для любого n.

Пример 1.

-ряд расходится по необходимому признаку сходимости.

Пример 2.

-ряд сходится по признаку Даламбера.

Пример 3.

интеграл расходится, значит, и ряд расходится по интегральному признаку Коши.

Пример 4.

Применим интегральный признак Коши.

= интеграл сходится, значит, и ряд тоже сходится.

Пример 5.

Применим признак Даламбера:

-значит ряд сходится.

Пример 6.

Ряд сходится по признаку Даламбера.

Пример 7.

По Даламберу:

= ряд расходится.

Пример 8.

Т.к. , а ряд , то ряд тоже расходится по признаку сравнения.

Пример 9.

, т.к. ряд расходится по интегральному признаку Коши, то и ряд

тоже расходится по признаку сравнения.

Пример 10.

Т.к. , а ряд сходится по признаку Даламбера, то

тоже сходится по признаку сравнения.

Пример 11.

Найти сумму ряда

Т.к. , то исходный ряд можно представить в виде:

Знакочередующиеся ряды.

Определение: Ряды вида

(3)

где знаки строго чередуются, называются знакочередующимися.

Теорема Лейбница.

Если в знакочередующемся ряде (3):

а) члены ряда убывают, т.е.

б) общий член стремится к нулю, при n стремящимся к бесконечности, т.е.

, то ряд (3) сходится, его сумма положительна и не превышает первого члена ряда.

Доказательство:

Рассмотрим частную сумму первых n=2m членов ряда. Представим её в виде:

>0 >0 >0

и возрастает с возрастанием m; с другой стороны,

Т.е. получим, что частные суммы возрастают и ограничены сверху числом

Для нечетных частичных сумм имеем.

Т.к. , то

Вывод: Ошибка при замене суммы сходящегося знакочередующегося ряда с убывающими по абсолютной величине членами суммой нескольких его первых членов меньше абсолютного значения первого из отброшенных членов.

Пример 1.

а)

б)

(два раза мы применили правило Лопиталя для ).

Т.е. знакочередующийся ряд сходится по признаку Лейбница.

Тогда ; - абсолютная погрешность,

;

;

Пример 2.

- необходимый признак сходимости выполнен

интеграл расходится по интегральному признаку Коши.

;

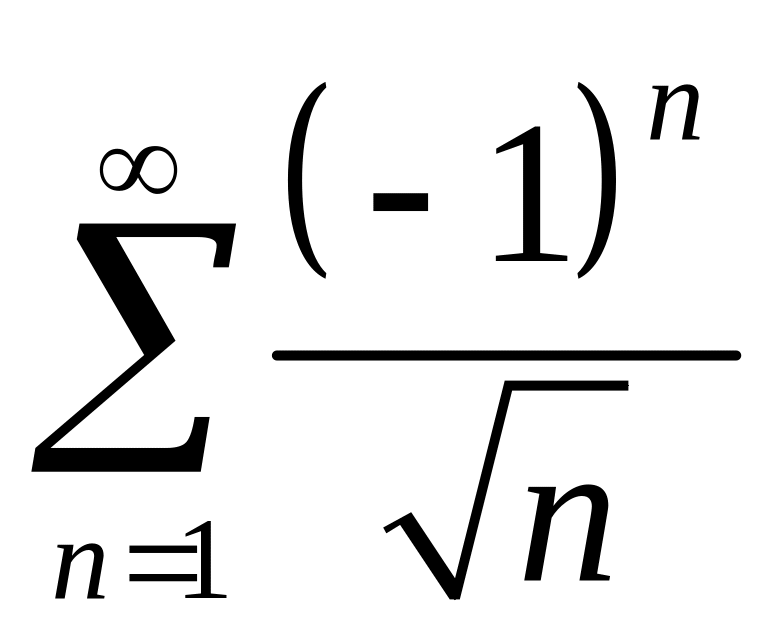убывают, , выполняются условия т. Лейбница – значит, ряд сходится.

Пример 3.

Интегральный признак Коши.

интеграл расходится, значит ряд тоже расходится.

Для ряда ; убывает, - выполняются условия т. Лейбница,

значит ряд сходится.

Пример 4.

, необходимый признак сходимости выполнен.

Ряд расходится по интегральному признаку Коши.

Пример 5.

Т.к.

- расходится, то тоже расходится по признаку сравнения.

Пример 6.

-ряд сходится по признаку Даламбера.

Пример 7.

Т.к. ,

а - сходится, по интегральному признаку Коши.

, то ряд тоже сходится по признаку сравнения.