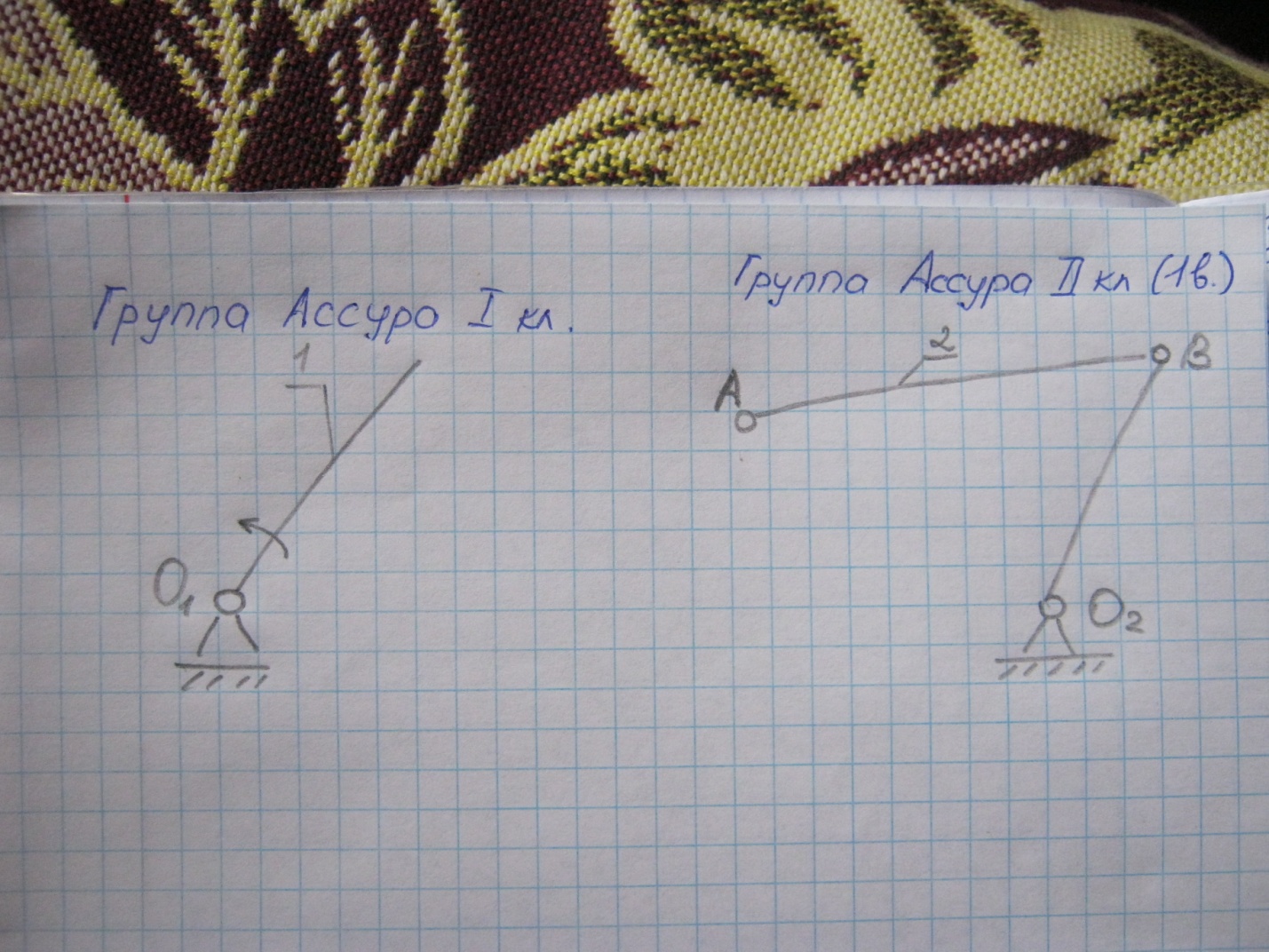
Структурный анализ механизма:

26. Синтез механизмов, его основные задачи. Синтез зубчатых механизмов с эвольвентным профилем зубьев. Основная теорема теории зацепления. Условие постоянства мгновенного передаточного отношения.

Задачей синтеза механизма является проектирование его кинематической схемы. Исходными данными дня синтеза являются кинематическая схема и заданные кинематические и динамические условия (свойства) механизма.

При синтезе определению подлежат постоянные параметры схемы механизма (размеры звеньев), при которых выполняются заданные свойства.

Синтез механизма предшествует выбору материалов звеньев, расчетам на прочность и жесткость конструктивному оформление звеньев и кинематических пар и т.п.

Как правило, при синтезе для получения заданных свойств механизма необходимо удовлетворить многим, часто противоречивым условиям, связанным с назначением механизма, его эксплуатацией, технологией изготовления и т.п. Обычно одно из условия является основным. Его достижение является обязательным. Все другие условия являются дополнительными.

Зубчатые механизмы предназначены для передачи вращательного движения и преобразования его параметров.

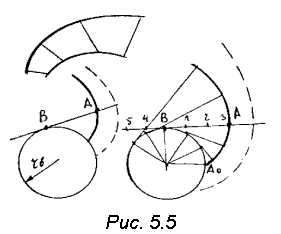
Геометрическое место центров кривизны какой-либо кривой называют инволютой, а саму кривую – эвольвентой (рис. 5.5). При профилировании зубьев в качестве эволюты используется окружность, называемая в дальнейшем основной, а сам зуб очерчивается эвольвентой окружности. Единственным параметром, отличающим одну эвольвенту от другой, является радиус основной окружности.

Можно указать следующий способ образования эвольвенты. Выбирается основная окружность rb, касающаяся ее производящая прямая и чертящая точка на ней. Перекатывая производящую прямую по окружности без скольжения, получаем траекторию чертящей точки, которая является эвольвентой, т.к. мгновенные радиусы кривизны ее лежат на основной окружности. Эвольвенту можно получить, наматывая нить с чертящей точкой на диск (рис. 5.5). Две чертящие точки дадут две эквидистантные (равноотстоящие) эвольвенты.

Из определения эвольвенты и из указанных выше способов ее построения вытекают следующие очевидные свойства:

1. Нормаль эвольвенты касается основной окружности.

2. Радиус кривизны эвольвенты равен длине нормали.

3. Длина нормали эвольвенты равна длине соответствующей дуги основной окружности

4. Расстояние между эквидистантными эвольвентами равно длине соответствующей дуги основной окружности

Основного закона зацепления: для постоянства передаточного отношения необходимо, чтобы нормаль, проведенная через точку касания двух профилей, пересекала межосевую линию в постоянной точке (полюсе зацепления). Иными словами требуется неизменность положения полюса.

Передаточным отношением называется отношение угловых скоростей колес, принято обозначать буквой U и снабжать индексами, указывающими номера зубчатых колес, например U12 = ω1 ⁄ ω2. Передаточному отношению присваивается знак +, если входное и выходное колеса вращаются в одном направлении, и знак -, если они вращаются в разном направлении. При передаточном отношении больше единицы имеем редуктор (замедление скорости), при передаточном отношении меньше единицы – мультипликатор (происходит увеличение скорости вращения). Передаточное отношение рядовой зубчатой передачи равно произведению передаточных отношений входящих в нее зубчатых передач, при этом следует учитывать знаки передаточных отношений составляющих зубчатых передач. Передаточное отношение рядовой зубчатой передачи равно дроби, в числителе которой стоят числа зубьев выходных колес, а в знаменателе – входных.