19Методика построении и определения диаграмм приведенных моментов и работ сил полезного сопротивления и движ. Сил.Сущность метода графич. Интегр.

Граф. интегрирование методом площадей

Этот метод основан на геом-ой интерпретации (физическом смысле) интеграла. Рассмотрим данный метод на прим. интегр. диаграммы скоростей. В рез-те интегр-ия необходимо построить диаграмму перемещений.

где А – площадь под кривой скорости на выделенном участке (что соответствует физическому смыслу интеграла).

Для интегрирования методом площадей выделяют на оси абсцисс N положений (в пределах одного цикла). Определяют площадь А₁  (в мм²) под графиком скорости на участке 0-1, площадь А₂ – на участке 1-2, площадь А₃ – на участке 2-3 и т.д. 

Умн-ив. эти площади на масштаб скоростей и масштаб времени диагр. скоростей, получают истинные перемещения на выделенных участках, по которым определяют общие перемещения в каждом положении исслед-ого звена в расчете от нул-го положения:

S_0-1 = K_{v *} K_t * A₁;   S_1-2 = K_{v *} K_{t *} A₂;   S_2-3 = K_{v *} K_{t *} A₃; и т.д.

S₁= S_0-1;    S₂= S₁ + S_1-2;    S₃= S₂ + S_2-3;  и т.д.

После определения всех перемещений задают масштаб K_s, в кот-ом строят диаг-му переем-ий.

Графическое интегрирование методом хорд

Данный метод основан на том, что интег-ние есть процесс обратный диффер-нию. Поэтому при этом методе производятся все те же действия, что и при диффер-нии методом хорд, только в обратном порядке:

- делят интегр-мую кривую на ряд участков;

- находят среднее знач. ф-ции на каждом участке (приближенно можно принимать за среднее значение функции посередине данного участка);

- сносят эти средние значения на ось ординат интегрируемой диаграммы;

- слева от начала координат на оси абсцисс отмечают полюс Р на некотором полюсном расстоянии H;

- соединяют полюс Р с отмеченными на оси ординат точками, характеризующими средние значения интегрируемой функции на выделенных участках. Полученные лучи характеризуют направления хорд на соответствующих участках искомой функции;

- из начала координат проводят хорду на первом участке, параллельную первому лучу; из конца первой хорды на втором участке проводят хорду, параллельную второму лучу и т.д.

В рез-те, после постр-ия всех хорд, формируется ломаная кривая, по вершинам кот-ой надо провести плавную кривую. При интег-нии диаг-ы скорост. получен. кривая будет представлять собой диагр-му перемещений (соответственно, при интег-нии диаг-мы уск-ий, получается диаг-ма скор.). Масштабы полученных диаграмм опред-ся из  зависимостей, выведенных для граф-го диффер-ния:

K_s = K_{v *} K_{t *} H

K_v = K_{a *} K_{t *} H₁

Этапы работы

1.По формуле 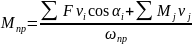определяем значение привед. момента ПС и строится график М_пр=f(φ)

2.Графическим интегрированием получ-го гр-ка получаем зависимость А_пс=f(φ)

3.Учитывая, что А_пс=А_дв получаем график А_дв=f(φ)

4.Графич-им дифференцированием ф-ции А_ДВ=f(φ) получаем граф. М_ДВ=f(φ) и его значения

6,7,8,9- положение механизма на протяжении рабочего хода

; ;

; ;

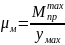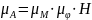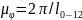
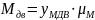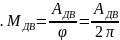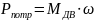
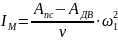
20. Применение принципа д’Аламбера в динамике машин. Главный вектор и главный момент сил инерции звена при различных случаях его движения

Если действовать на точку активными силами и реакциями связей присоединить силу инерции то полученную систему сил можно считать уравновешенной. ∑F_i =ma; F-ma=0;∑F_i + F^и=0

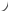
a F^и F Применение рычага Жуковоского для определения уравновешивающей силы. ∑P_i=0; ∑ F_iV_icosα+∑M_iW_i=0; Применив принцип Даламбера данное уравнение можно решить аналитически, но гораздо проще применив метод Жуковского F_i α_i V_i h_i α P P_i= F_i V_i cos α= F_i h_i h_i = V_i cos α F_ур h_ур + ∑ F_i h_i F_ур=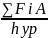

21. Методика определения уравновешивающей силы при помощи вспомогательного рычага Н.Е. Жуковского.

Применив принцип Даламбера

.

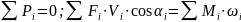Данное уравнение можно решить аналитически, но гораздо проще применив способ Жуковского

;

;

;

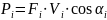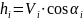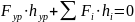22.Изобразите кинематическую схему, приведите название звеньев и произведите структурный анализ кулачкового механизма

1 – Кулочек. 2 – Толкатель. 3 – Неподвижное звено.

23. Изобразите кинематическую схему, приведите название звеньев и произведите структурный анализ кулисного механизма

1 – кривошип

2 – ползун (кулисный камень)

3 – кулиса

4 – шарнир

Структурный анализ.

W=3n-2p₅-p₄ где: n – число всех подвижных звеньев механизма; p₅ – количество пар 5 класса; p₄ – количество пар 4 класса; n = 5; р₅ = 7 W=3·5-2·7=1

24.Изобразите кинематическую схему , приведите названия звеньев и произведите структ-ый анализ кривошипно – ползунного механизма

Для 2 рис.- 1-коленчатый вал; 2 – шатун; 3- поршень

Структурный анализ

Состоит из 1-го подв. звена и 1-ой кинем. пары

звено ОА и АВ относятся к I группе Ассура, поэтому механизм относится к 1-ому классу.

25. Изобразите кинематическую схему, приведите названия звеньев и произведите структурный анализ кривошипно-коромыслового механизма.

1-кривошип

2 – шатун

4 – станина, основание

Это механизм для преобразования одного вида движения в другое. Он преобразовывает вращение кривошипа в качательное движение коромысла.