
- •1.Основные задачи и понятия тмм. Машина, механизм, кп, кц, их классификация
- •1)Энергетические 2) рабочие 3) информационные
- •2.Структура механизмов. Деталь, звено, кинематическая пара, кинематическая цепь, их классификация.
- •3.Классификация кинематических пар по характеру соприкосновения
- •4 Классификация кинематических пар по числу условий связей
- •5.Структурная формула кинематической цепи общего вида ( Сомова-Малышева)
- •6.Структурная формула плоских механизмов (Чебышева). Методика определения степени подвижности плоских механизмов
- •7.Классификация механизмов по Ассуру. Группы Ассура, их классификация. Основной принцип образования плоских механизмов
- •8. Кинематический анализ(ка) механизмов, его основные задачи и методы. Параметры, определяемые в ходе ка
- •9. Планы положений механизма.Кинематические диаграммы. Сущность метода графического дифференцирования.
- •10.Применение планов скоростей при выполнении кинем. Анализа плоского шарнирно- рычажкового механизма……
- •2.1.1. Определение скоростей
- •12. Динамический анализ механизмов, его основные задачи. Классификация сил, действующих на звенья механизма.
- •Обратная
- •13. Уравновешивающая сила. Формулы, применяемые для определения величины уравновешивающей силы, уравновешивающего момента, потребной мощности двигателя.
- •14. Основные режимы работы механизма.
- •15. Неравномерность хода механизмов в установившемся движении. Коэффициент неравномерности хода машины
- •16) Приведённая масса. Приведённый момент инерции массы. Приведение сил и моментов сил к звену приведения. Причина широкого применения метода приведения сил и массы в динамике машин
- •17. Определение величины момента инерции маховика, обеспечивающий необходимый коэффициент неравномерности хода машины. Методика и вывод основных формул.
- •18)Уравнение движения машины, его использование в динамическом анализе.
- •19Методика построении и определения диаграмм приведенных моментов и работ сил полезного сопротивления и движ. Сил.Сущность метода графич. Интегр.
- •20. Применение принципа д’Аламбера в динамике машин. Главный вектор и главный момент сил инерции звена при различных случаях его движения
- •Структурный анализ механизма:
- •27. Методика построения эвольвентного профиля зубьев. Докажите, что при эвольвентном профиле зубьев мгновенное передаточное отношение остаётся постоянным.
- •28) Геометрические элементы зубчатых колёс. Шаг зацепления, модуль зацепления.
16) Приведённая масса. Приведённый момент инерции массы. Приведение сил и моментов сил к звену приведения. Причина широкого применения метода приведения сил и массы в динамике машин
Приведенная масса – такая условная масса, сосредоточенная в точке приведения на ведущем звене, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.
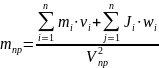
На ряду с понятием приведенной массы используется понятие приведённого момента инерций в том случае если ведущее звено совершает вращающее движение
Jпр=mпр-l2
l – расстояние от вращающего звена до точки приведения
Метод приведённых сил, также как и метод приведённых масс часто исп. В динамике машин, т.к. позволяет значительно упростить задачу динамического движения всех звеньев механизма, сведя её к задаче движения одного звена – звена приведения.
В качестве звена приведения выбирается ведущее звено, например главный вал машины.
Приведённая сила – угловая сила приложенная к ведущему звену и развивающая в данном положении механизма мощность равную сумме мощностей всех действующих на звенья механизма сил и моментов сил в данном его положении
Pпр=∑Pi Pпр=Fпр ∙Vпр
На ряду с понятием приведённой силы исп. понятие приведённого момента сил: Мпр=Fпр∙Loa
17. Определение величины момента инерции маховика, обеспечивающий необходимый коэффициент неравномерности хода машины. Методика и вывод основных формул.
Потребный коэффициент
неравномерности хода для различных
механизмов и машин, для технологических
механизмов рекомендуется δ=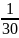 …
…
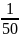 ,
в двигателях внутреннего сгорания и
компрессорах δ=
,
в двигателях внутреннего сгорания и
компрессорах δ=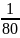 …
…
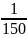 .
.
Таких значений δ установив маховик на ведущее звено и главный вал.
Маховик – колесо имеющее тяжелый обод.
Основные требование:
Момент инерции и
маховика должен быть больше приведенного
момента инерции всех остальных звеньев,
так как суммарный приведенный момент
инерции
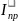 =
= +
+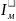 , при этом момент инерции маховика
постоянен и момент инерции маховика на
много больше приведенного момента
инерции всех звеньев, таким образом
увеличится приведенная масса и уменьшается
угловую скорость относительно средней
угловой скорости
, при этом момент инерции маховика
постоянен и момент инерции маховика на
много больше приведенного момента
инерции всех звеньев, таким образом
увеличится приведенная масса и уменьшается
угловую скорость относительно средней
угловой скорости
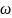 ср . Тогда пренебрегаем приведенного
момента инерции всех звеньев
,
тогда максимальная кинетическая энергия
механизма.
ср . Тогда пренебрегаем приведенного
момента инерции всех звеньев
,
тогда максимальная кинетическая энергия
механизма.
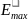 =
=
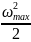 ;
;
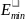 =
=
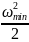 ;
-
=
E=
;
-
=
E=
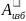 =
=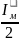 (
(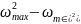 );
);
=
2
δ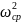 =
δ
;
=
=
δ
;
=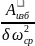
Где
=
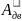 -
-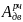 , т. к. речь идет об установившемся
движении
, т. к. речь идет об установившемся
движении
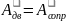 работа движения равна работе сопротивления.
работа движения равна работе сопротивления.
=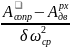 где
где
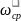 =
=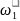 ,
=
,
=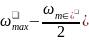 и
=
и
=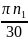
коэффициент
неравномерности хода δ=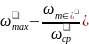
18)Уравнение движения машины, его использование в динамическом анализе.
Уравнение движения машины (основное уравнение динамики машин) представляет собой теорему об изменении кинетической энергии материальной системы:
Е-Ео=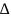 Е-
Е-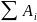 =АДв.-АВр.
сопр.-Апол.
сопр.
=АДв.-АВр.
сопр.-Апол.
сопр.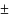 А(G)=
А(G)=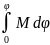 (1)
(1)
где Ео-кинетическая энергия звеньев механизма в начальный момент.
В случаи установившегося движения: Е= = =0 (2)
При практических расчетах значениями АВр. сопр. и А(G) часто пренебрегают в следствии их относительной малости
Уравнение приобретает вид:
АДв.-
Апол.
сопр.=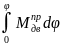 -
-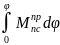 =0
(3)
=0
(3)
При помощи уравнения (3) можно определить по известным силам полезного сопротивления момент движущих сил Мдв. -крутящий момент двигателя, а также Адв. и Апол. сопр.. Следовательно определяется Рпотр.-потребная мощность двигателя для данного механизма и Iм-момент инерции маховика, обеспечивающий равномерное движение кривошипа с заданным коэффициентом неравномерности .
