Елементи теорії функцій та функціонального аналізу

1. Еквівалентні множини. Потужність множини. Порівняння потужностей.

2. Зчисленні множини та їх властивості.

3. Незчисленність множини дійсних чисел [0; 1]. Множини потужності континууму та їх властивості.

4. Граничні точки множини. Замкнені множини, властивості замкнених множин.

5. Відкриті множини, властивості відкритих множин.

6. Структура відкритих, замкнених підмножин множини дійсних чисел.

7. Множина Кантора, підмножини і та їх властивості.

8. Задача вимірювання множин. Зовнішня і внутрішня міри Лебега та їх властивості.

9. Вимірні за Лебегом множини. Приклади вимірних множин. Властивості вимірних за Лебегом множин.

10. Вимірні функції. Приклади вимірних функцій. Властивості вимірних функцій.

11. Коливання функцій на множині і в точці. Неперервність функції за Бером. Критерій інтегровності функцій за Ріманом.

12. Означення інтеграла Лебега та умови його існування.

13. Основні властивості інтеграла Лебега. Зв’язок інтеграла Рімана з інтегралом Лебега.

14. Збіжність майже скрізь і збіжність за мірою. Граничний перехід під знаком інтеграла Лебега.

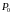15. Інтеграл Лебега від невід’ємної необмеженої вимірної функції та його властивості. Сумовні функції довільного знака.

1. Еквівалентні множини. Потужність множини. Порівняння потужностей.

Взаємо-однозначна відповідність. Еквів. множин.

Озн. Відображенням 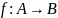називається закон, за яким кожному елем. 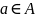ставиться у відповідність єдиний ел. . Множина A називається множиною визначення відоб. f. .

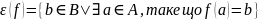Озн. Відображенням назив. ін’єкцією, якщо з умови

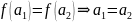
Озн. Відображенням назив. сюр’єкцією, якщо з умови .

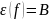Озн. Відображенням назив. бієкцією, якщо f ін’єкція і сюр’єкція.

Теорема. Якщо бієкція, то тоді визначено обер відображ 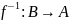- бієкція.

Дов. .

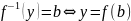1. f – обернене відображення? , але f – ін’єкція, тому .

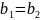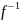2. – ін’єкція?

Якщо 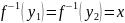, то тоді .

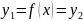3. – сюр’єкція?

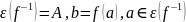, а отже, – сюр’єкція. Доведено.

Потужність множин. Порівняння потужностей.

Озн. Говорять, множини мають однакову потужність(або та 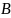еквівалентні), якщо 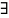відобр. , таке що – бієкція.

Відношення A~B еквівалентне, якщо

1. A~A Потрібно побудувати 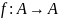. 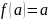- буде бієкцією.

а) якщ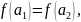о то і f – ін’єкція;

б) очевидно, що 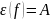, тому – сюр’єкція, а отже, – бі’єкція

2. Із A~B випливає B~A

- бієкція, за теорем про обернене відображення – бієкція, а отже B~A.

3. Із A~B і B~C випливає A~C

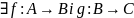, покажемо, що знайдеться бієктивне відображення , тобто задається складене відображення g(f), що діє .

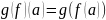а) Оскільки g- ін’єкція, то маємо 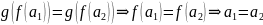, бо f – ін’єкція. Отже, g(f) – ін’єкція.

б) Доведемо, що 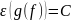. Для цього нехай дано елем. . Раз g – сюр’єкція, 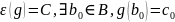. Раз f – сюр’єкція, то 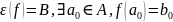. Остаточно 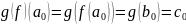і 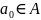. Доведено, що , отже, g(f) – сюрєкція, а отже, g(f) – бієкція. Тим самим всі множини розбиваються на класи еквівалентних множин.

Якщо маємо відображення і кількість елементів множини A – n, множини B – m, то з умови f – ін’єкція ви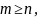пливає а з умови f – сюр’єкція випливає 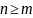, а так як f – бієкція, то 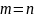, тобто еквівалентними будуть скінченні множини з однаковою кількістю елементів.

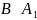Теорема Кантора-Бернштейна. Якщо дві непорожні мн. A та B і - підмножина B, а – підмножина A, то тоді A~B.

Доведення.

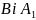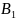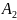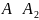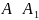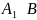Розглянемо взаємно-однозначну відповідність між , тоді підмножині буде відповідати підмножина , причому , тобто . А так як і то за транзитивністю . , , отже, A~B. Доведено.