2.3. Изгиб (кривизна)
Дюрация дает приемлемую оценку изменения цены облигации при небольшом изменении доходности до погашения, так как график цены облигации имеет вогнутую форму (см. рис. 1). Для более точной оценки изменения цены облигации следует учесть такой показатель как изгиб (convexity), обозначим его через Сonv. Изменение цены облигации можно разложить на составляющие части с помощью ряда Тейлора. Для решения нашей задачи возьмем два первых слагаемых данного ряда. Тогда изменение цены облигации можно представить следующим образом:
.
(2.34)
Изгиб равен:
.
(2.35)
Вторая производная цены облигации по
процентной ставке
определяется следующим образом:
.
(2.36)
Подставив выражение второй производной (2.36) в (2.35) получим формулу расчета изгиба (кривизны):
.
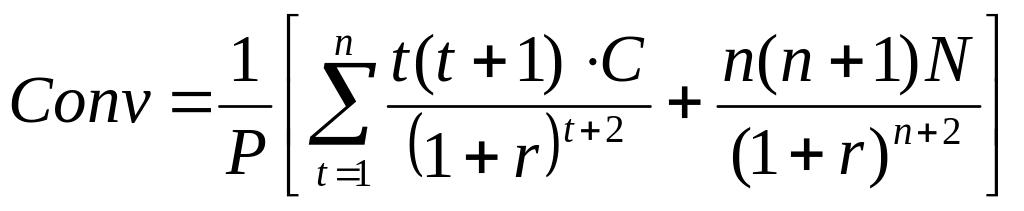(2.37)
Если купоны по облигации выплачиваются m раз в году, то кривизну следует вычислять по формуле:
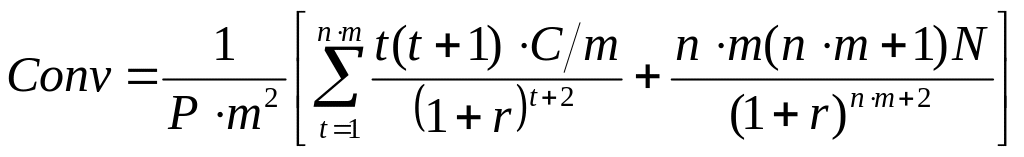(2.38)
С учетом модифицированной дюрации и изгиба процентное изменение цены облигации можно определить следующим образом:
.
(2.39)
Использование модифицированной дюрации и изгиба позволяют довольно точно определить процентное изменение цены облигации при существенном изменении доходности до погашения.
Изгиб характеризуется следующими особенностями.
1) Его величина возрастает при уменьшении доходности до погашения и падает при его росте.
2) При данном значении доходности до погашения и времени погашения величина изгиба больше для облигаций с более низким купоном.
3) При данном значении доходности до погашения и модифицированной дюрации величина изгиба меньше для облигации с более низким купоном.
4) Величина изгиба возрастает в большей степени чем при росте дюрации.
Изгиб — один из важных инвестиционных качеств облигации, особенно в условиях нестабильности процентных ставок. Он говорит о величине кривизны графика цены облигации, что наглядно представлено на рис. 2. Облигации А и В имеют одинаковую дюрацию, но величина изгиба облигации В больше чем облигации А. Это свидетельствует о том, что при падении доходности цена облигации В вырастет в большей степени, чем облигации А. При росте доходности ее цена упадет в меньшей степени, чем облигации А. Таким образом, с точки зрения инвестиционных качеств, облигация В лучше облигации А. Они мало заметны при небольшом изменении доходности до погашения, однако проявляются в существенной степени при значительном изменении процентной ставки. Поскольку облигация В дает инвесторам преимущество, то она должна оцениваться на рынке. Поэтому цена облигации В будет больше цены облигации А, и эта разница проявится тем сильнее, чем определеннее ожидания инвесторов относительно неустойчивости конъюнктуры.
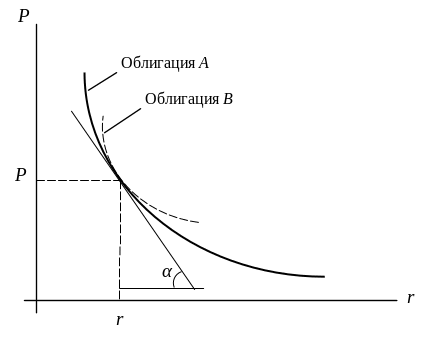
Рис. 2.2. Изгиб
Решение типовых задач
Задача 1.
Номинал облигации равен 1 млн. руб., купон — 20%, выплачивается один раз в год, до погашения остается три года. На рынке доходность на инвестиции с уровнем риска, соответствующим данной облигации, оценивается в 25%. Определить курсовую стоимость бумаги.
Решение:
1) Определяем поток доходов, который принесет облигация инвестору за три года. В конце каждого года инвестор получит купон в сумме 200 тыс. руб., и в конце третьего года ему выплатят сумму номинала в размере 1 млн. руб. Таким образом, облигация принесет следующий поток доходов:
Год |
1 |
2 |
3 |
Сумма, тыс. руб. |
200 |
200 |
1000+200=1200 |
2) Определяем дисконтированную стоимость суммы каждого платежа по облигации. Для первого платежа она равна:
тыс. руб.
Для второго платежа:
тыс. руб.
Для третьего платежа:
тыс. руб.
3) Определяем цену облигации:
Р=160 + 128 + 614.4 = 902.4 тыс. руб.
Точно такой же ответ можно получить, используя формулу (2.1):
руб.
Задача 2.
Номинал облигации 1000 руб., купон 11%, выплачивается два раза в год. До погашения 3 года. Определить цену облигации, если ее доходность до погашения должна составлять 7%.
Решение:
Если купон выплачивается m раз в год, то цен облигации вычисляется по формуле:
,
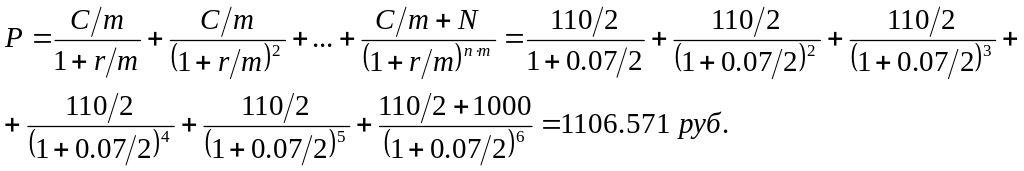где
руб.
Задача 3.
Номинал облигации 1000 руб., купон 12%, выплачивается один раз в год. До погашения 3 года 250 дней. Определить цену облигации, если ее доходность до погашения должна составлять 9%. База 365 дней.
Решение:
Цена облигации вычисляется по формуле (2.6):
Задача 4.
Номинал облигации 1000 руб., купон 14%, выплачивается один раз в год. До погашения 17 лет. Определить цену облигации, если ее доходность до погашения должна составлять 12,5%.
Решение:
Цена облигации вычисляется по формуле (2.4):
Задача 5.
Номинал облигации 1000 руб., купон 12%, выплачивается два раза в год. До погашения 7 лет. Определить цену облигации, если ее доходность до погашения должна составлять 8,5%.
Решение:
Цена облигации вычисляется по формуле (2.5):
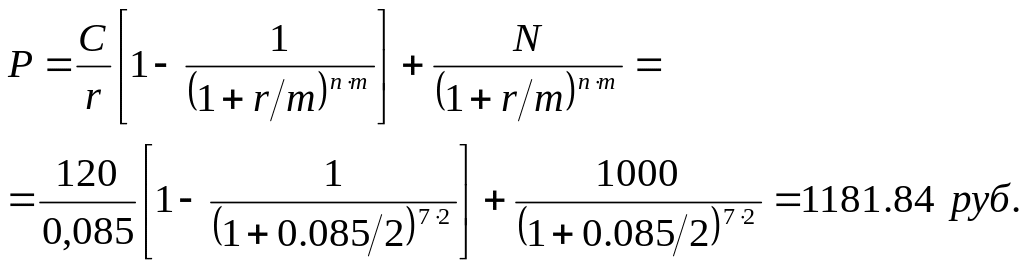
Задача 6.
Номинал облигации 1000 руб., купон 8%, выплачивается один раз в год. До погашения 11 лет и 45 дней. Определить цену облигации, если ее доходность до погашения должна составлять 12%. База 365 дней.
Решение:
Если до погашения облигации остается не целое число лет, что формулу (2.4) можно преобразовать к виду:
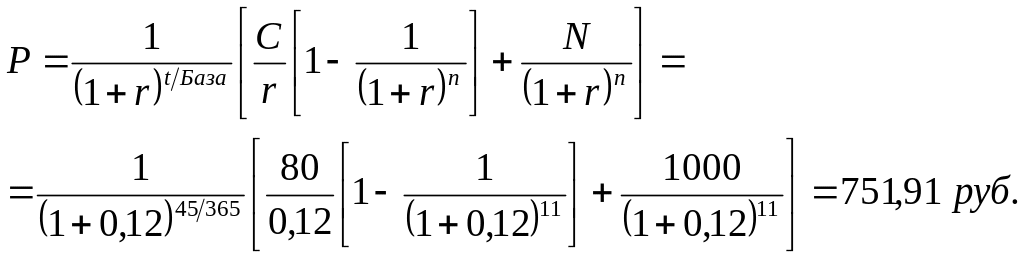
Задача 7.
Номинал бескупонной облигации равен 1000 руб., бумага погашается через 6 лет. Определить цену облигации, если ее доходность до погашения должна составлять 13% годовых.
Решение:
Цена бескупонной облигации вычисляется по формуле (2.8)
Задача 8.
Номинал бескупонной облигации равен 1000 руб., бумага погашается через 6 лет и 30 дней. Определить цену облигации, если ее доходность до погашения должна составлять 14% годовых. База 365 дней.
Решение:
Цена бескупонной облигации в данном случае вычисляется по формуле (2.9):
Задача 9.
Номинал бескупонной облигации равен 1000 руб., бумага погашается через 6 лет. Определить цену облигации, если ее доходность до погашения должна составлять 9% годовых. По купонным облигациям купоны выплачиваются два раза в год.
Решение:
Цена бескупонной облигации в данном случае вычисляется по формуле (2.10):
Задача 10.
Номинал бескупонной облигации равен 1000 руб., бумага погашается через 55 дней. Определить цену облигации, если ее доходность до погашения должна составлять 5% годовых. База 365 дней.
Решение:
Цена краткосрочной бескупонной облигации вычисляется по формуле (2.11):
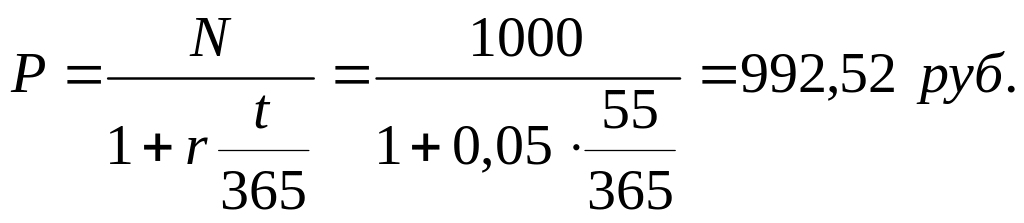
Задача 11.
Номинал облигации 1000 руб., купон 12%. Облигация стоит 947 руб. Определить текущую доходность облигации.
Решение:
Текущая доходность облигации определяется по формуле (2.12):
или 12,67% годовых.
Задача 12.
Номинал бескупонной облигации 1000 руб., бумага погашается через 4 года. Облигация стоит 790 руб. Определить доходность до погашения облигации.
Решение:
Доходность до погашения облигации с нулевым купоном определяется по формуле (2.15):
или 6,07% годовых.
Задача 13.
Номинал бескупонной облигации 1000 руб., бумага погашается через 3 года и 160 дней. Облигация стоит 740 руб. Определить доходность до погашения облигации. База 365 руб.
Решение:
Доходность до погашения облигации с нулевым купоном определяется по формуле:
или 9,15% годовых.
Задача 14.
Номинал бескупонной облигации 1000 руб. Облигация погашается через три года. Инвестор купил облигацию по 845 руб. и продал через 140 дней по 883 руб. Определить доходность операции инвестора в расчете на год на основе: 1) простого процента; 2) эффективного процента. База 365 дней.
Решение: