4.4. Оптимизация планирования поставок с учетом требований к безотказности

Поскольку сеть поставок может формироваться из каналов с разными характеристиками, модель структурной надежности сети в общем случае будет включать как отдельные каналы, так и цепочки, а также целые подсети поставок довольно сложной структуры (рис. 8.11).

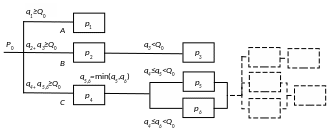
Рис. 8.11. Многоуровневая сложно структурированная модель схемной надежности сети поставок

Формирование подсетей структуры C и более сложных (см. рис. 8.11) в процессной модели управления поставками нецелесообразно в силу трудности контроля и обеспечения необходимого уровня надежности. Из этих подсетей поставщиками 2-го уровня могут быть созданы дополнительные цепочки простой, последовательной структуры, предлагаемые заказчику на условиях аутсорсинга. Иными словами, упрощение структуры сети путем интеграции каналов поставок возлагается на поставщиков 2-го или еще более низкого уровня. Для заказчика задача формирования сети поставок трансформируется в задачу выбора наиболее экономически выгодных каналов при условии соблюдения требований к функциональным параметрам (например, объему) и безотказности, определяемой по формуле для простой, последовательно-параллельной схемы, представленной на рис. 8.12

,

где n – количество поставщиков; m – количество цепочек поставок (каналов); – бинарная переменная (переменная выбора), принимающая значение 1, если мощность j-ых поставщиков, включенных в i-й канал поставки позволяет удовлетворить спрос , либо 0 – если нет, т.е. . Бинарная переменная служит для формирования m цепочек из n каналов.

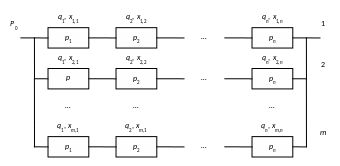
Рис. 8.12. Последовательно-параллельная модель структурной надежности сети поставок

В частном случае при n = m модель структурной надежности сети поставок состоит из n параллельно соединенных каналов мощностью .

Таким образом, предлагается использовать логико-вероятностный метод анализа для формирования многоуровневых сложно структурированных моделей сети поставок.

Введем в рассмотрение переменные представляющие величину поставок товара от j-ого поставщика, включенного в i-й канал поставки. Тогда, оптимальный план поставок определяется в результате решения задачи математического программирования с целевой функцией:

(8.23)

и ограничениями

(8.24)

(8.25)

(8.26)

(8.27)

(8.28)

(8.29)

(8.30)

(8.31)

(8.32)

Целевая функция (8.23) представляет собой сумму переменных и постоянных затрат в данной системе управления поставками. В системе ограничений (8.24)-(8.32) ограничение (8.24) – требование к безотказности цепи поставок, состоящей из последовательно-параллельных элементов. Условие означает: если не 0, то в произведении используется значение . В противном случае не входит в произведение, т.е. перемножаются только вероятности каналов, входящих в цепочку. Ограничение (8.25) – требование к объему поставки: стандартное ограничение на общий объем поставок по всем каналам сети. Ограничение (8.26) – условие включения поставщика в один канал (одну цепочку) означает, что поставщик может входить только в один канал или не входить ни в одну их них (лишний канал). Ограничение (8.27) – ограничение по предложению поставщиков . Ограничение (8.28) – ограничение на минимальный заказ d, которое учитывает издержки, связанные с заключением договора поставки, т.е. является экономическим условием контракта. Ограничение (8.29) – условие формирования канала поставки: каждый канал должен обеспечивать поставку в объеме не менее , причем суммируются только объемы по поставщикам, входящим в канал, т.е., если не 0. Наконец, ограничение (8.30)-(8.32) указывают, что переменные являются неотрицательными действительными числами, а являются булевыми переменными.

Данная модель обеспечивает гибкость поставок с заданной безотказностью за счет возможности регулирования объемов поставок по каналам. При решении данной задачи возникает ряд проблем. Первой проблемой является расчет вероятности безотказной работы сети поставок P₀, требующий применения логико-вероятностного метода, т.е. описания всех работоспособных и неработоспособных состояний сети поставок с помощью функций алгебры логики (ФАЛ). Сложность заключается в большом количестве возможных функциональных состояний системы, особенно в многоуровневых сетях поставок. Вторая проблема связана с нахождением численного решения задачи (8.23)-(8.32). Математическая модель данной задачи относится к классу моделей смешанного программирования, поскольку переменные являются неотрицательными действительными числами, а являются булевыми переменными.

В работе [13] предложено решать указанные проблемы путем разбиения общей задачи (8.23)-(8.32) на ряд более простых задач и поэтапного их решении. На рис. 8.13 представлена блок-схема алгоритма решения задачи определения оптимального плана поставок с учетом требований к безотказности.

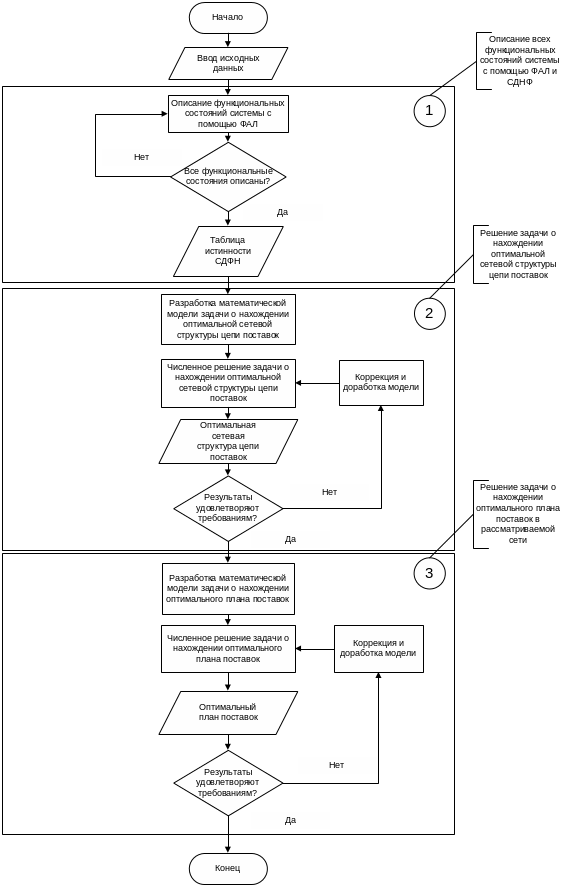
Рис. 8.13. Блок-схема алгоритма решения задачи определения оптимального плана поставок

Алгоритм решения задачи определения оптимального плана поставок включает следующие этапы:

1. описание всех функциональных состояний сети поставок с помощью ФАЛ и совершенной дизъюнктивной нормальной формы (СДНФ);

2. разработка модели линейного программирования и решение задача о нахождении оптимальной сетевой структуры цепи поставок;

3. разработка модели линейного программирования и решения задачи о нахождении оптимального плана поставок в рассматриваемой сети.

Рассмотрим более подробно этапы данного алгоритма.

Этап 1. Описание всех функциональных состояний сети поставок с помощью ФАЛ и СДНФ представляет проблему ввиду большого количества возможных вариантов структурной схемы системы.

Число возможных вариантов структурной схемы системы определяется следующим выражением:

,

где – число сочетаний из n элементов по k (k = 1,2, …, n) находится по формуле .

Например, если число поставщиков n = 6, то число возможных вариантов структурной схемы системы C = 63.

Этап 2. На данном этапе должна решаться задача о нахождении оптимальной сетевой структуры цепи поставок. Данная задача может быть сформулирована в виде модели линейного программирования.

Введем в рассмотрение булевы переменные , принимающие значения 1, если и значение 0, если , . Таким образом, является функцией двоичных переменных и принимает значение 1 лишь для тех наборов переменных , при которых удовлетворяется требование к формированию канала поставок. Введем также в рассмотрение булевы переменные , принимающие значение 1, если i-й канал включен в оптимальную сетевую структуры цепи поставок и значение 0 – если не включен, и переменные , принимающие значение 1, если j-й поставщик включен в оптимальную сетевую структуры цепи поставок и значение 0 – если не включен.

В соответствии с формулой (2) очевидно, что наиболее надежная сеть поставок должна включать максимально возможное количество независимых каналов поставок.

Тогда, оптимальная сетевая структура цепи поставок может быть найдена в результате решения следующей модели линейного программирования:

(8.33)

при ограничениях

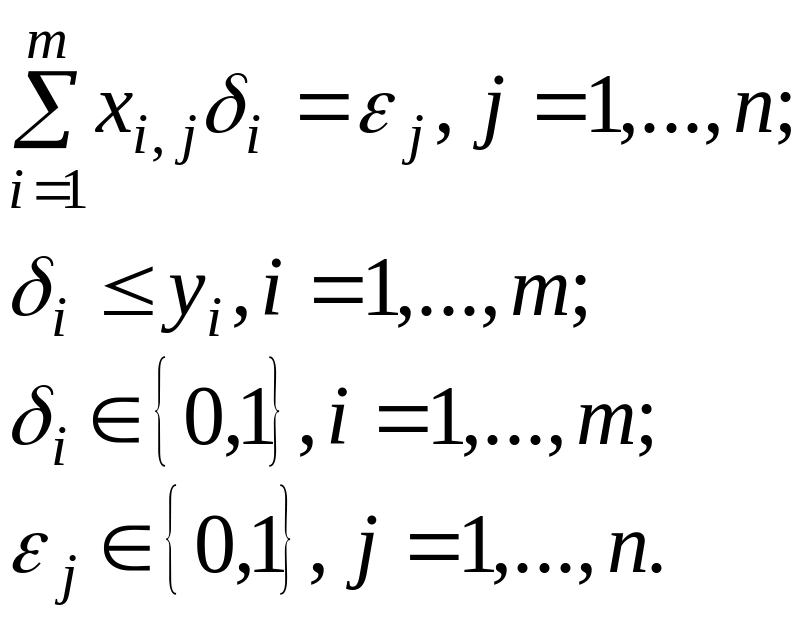
(8.34)

Первое ограничение в системе (8.34) гарантирует, что j-й поставщик будет включен только в один канал поставок либо не включен ни в один из них. Второе ограничение в системе (8.34) гарантирует, что в оптимальную сеть поставок будут включены только каналы удовлетворяющие требованию обеспечения заданного объема поставок. Третье и четвертое ограничения в системе (8.34) задают тип переменных и .

Полученное после оптимизации данной модели решение гарантирует выполнение условия . Очевидно, что при решении данной задачи в оптимальную сетевую структуру цепи поставок может быть включено избыточное число поставщиков. Чтобы избежать этого, необходимо создавать сценарии поиска решения, в которых переменная будет принимать задаваемые пользователем значения. Затем, из всех полученных решений необходимо выбрать такое, которое гарантирует выполнение условия с минимальным числом поставщиков, входящих в оптимальную сетевую структуру цепи поставок.

Этап 3. Затем, должна решаться задача определения оптимального плана поставок с учетом требований к надежности поставок. Данная задача также может быть сформулирована в виде модели линейного программирования. Допустим J – множество индексов поставщиков, включенных в оптимальную сетевую структуру цепи поставок, I – множество индексов каналов поставок, включенных в оптимальную сетевую структуру цепи поставок. Тогда, задача определения оптимального плана поставок с учетом требований к надежности поставок может быть сформулирована в следующем виде.

Найти минимум целевой функции

(8.35)

при ограничениях

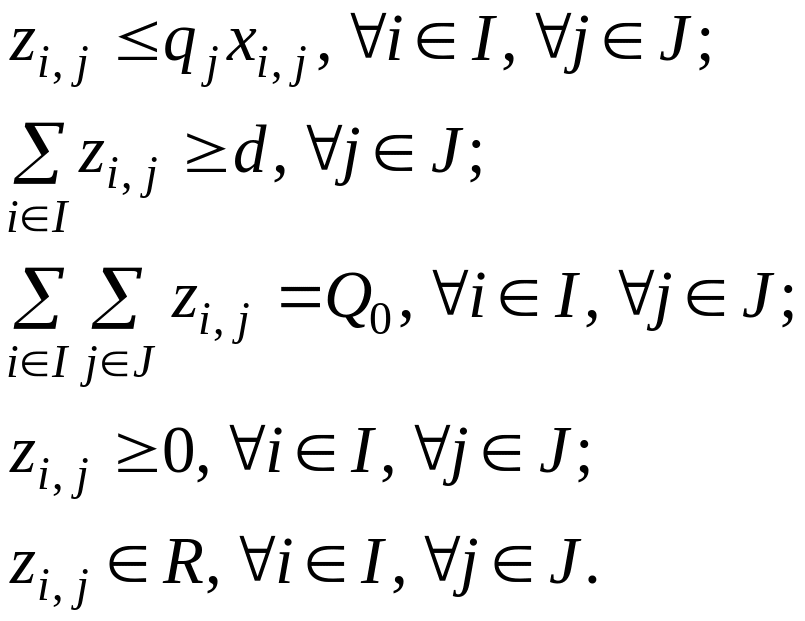
(8.36)

Целевая функция (8.35) представляет собой сумму переменных и постоянных затрат. Первая строка в системе ограничений (8.36) гарантирует, что поставка объемом будет осуществлена только в том случае, если j-й поставщик включен в i-й канал поставок. Вторая строка в системе (8.36) – это ограничения на минимальный заказ d. Третья строка в системе (8.36) – это ограничение на общий объем поставок по всем каналам сети. Последние две строки в системе ограничений (8.36) указывают, что являются неотрицательными действительными числами.

Таким образом, задача математического программирования (8.23)-(8.32) с переменными смешанного типа может быть представлена в виде двух моделей линейного программирования: модели (8.33)-(8.34) с булевыми переменными и , и модели (8.35)-(8.36) с переменными , являющимися неотрицательными действительными числами. Поскольку нахождение численного решения данных задач не представляет никакой проблемы, то представляется возможным нахождения оптимального плана поставок для моделей многоуровневых сложно-структурированных сетей поставок.

Математическая постановка задачи (8.35)-(8.36) может быть усложнена, например, в целевой функции может быть учтена величина возможного ущерба от недопоставок продукции. Тогда, целевая функция примет вид:

, (8.37)

где – вероятность отказа i-го канала, входящего в цепь поставок.

Рассмотренная проблема обеспечения безотказности каналов поставок товаров характерна для распределенных сетевых структур цепей поставок, ориентированных на активное использование технологии аутсорсинга бизнес-процессов. Возникающую в таких системах поставок сложную задачу планирования с учетом требований потребителя к безотказности по объемам и точности поставок можно путем логического анализа структур свести к достаточно легко решаемым задачам линейного программирования.